Demand and Inverse Demand Function | (How to find the INVERSE demand equation) | Think Econ

Think Econ
6 Jan 202305:18
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video clarifies the distinction between the demand equation and its inverse in economics. It begins with the standard downward-sloping demand curve, emphasizing the correct axis labeling. The script presents a linear demand equation, QD = 240 - 5P, and then demonstrates step-by-step the algebraic process of transforming it into the inverse demand function, P = 48 - 0.2Q. The video encourages viewers to practice this skill, highlighting the importance of understanding both functions for economic analysis.

Takeaways
  • 📈 The video discusses the difference between the demand equation and the inverse demand equation in economics.
  • 📊 It emphasizes the importance of correctly labeling axes with price on the Y-axis and quantity on the X-axis for a demand curve.
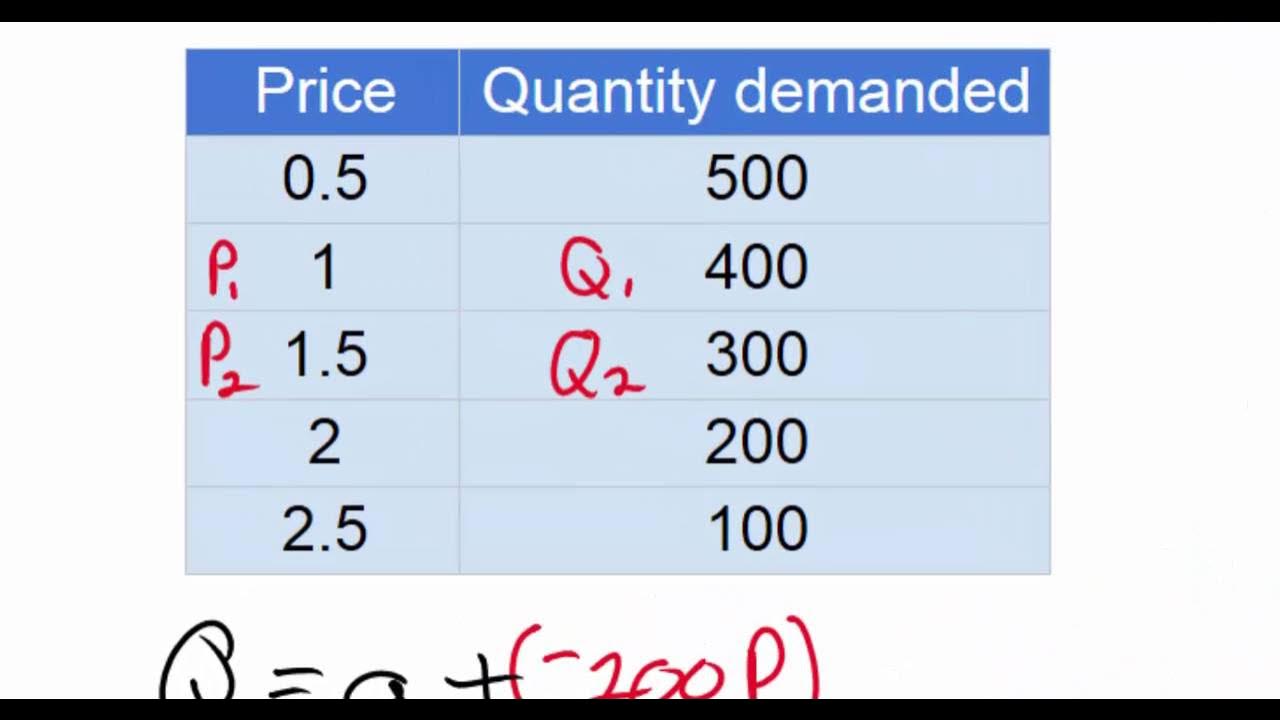
  • 🔍 The script provides an example of a general demand equation, QD = 240 - 5P, illustrating the negative relationship between price and quantity demanded.
  • 📚 The law of demand is mentioned, which states that there is a negative correlation between price and quantity demanded.
  • ✏️ The video demonstrates how to algebraically manipulate the demand equation to derive the inverse demand function.
  • 🔄 The process involves isolating P (price) and making it the dependent variable, which involves switching sides and changing signs.
  • 📝 The inverse demand function is derived to be P = 48 - 0.2Q, showing price as a function of quantity demanded.
  • 📉 The video explains that the inverse demand function is not just a different form but a rearrangement of the original demand equation.
  • 📈 It clarifies that in economics, the demand curve typically represents the inverse demand function, even though the original equation is used for algebraic solutions.
  • 📚 The script encourages viewers to practice deriving the inverse demand function from any given demand equation and vice versa.
  • 👍 The video concludes by inviting viewers to engage with the channel through likes, subscriptions, and comments for future topic suggestions.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is explaining the difference between the demand equation and the inverse demand equation in economics.

  • Why is it important to label the axes correctly when drawing a demand curve?

    -It is important to label the axes correctly because placing price on the vertical axis (y-axis) and quantity on the horizontal axis (x-axis) is a standard in economics. Mislabeling can lead to confusion and loss of marks in assessments.

  • What is the general form of a demand equation as presented in the video?

    -The general form of the demand equation presented in the video is QD = 240 - 5P, where QD represents the quantity demanded and P represents the price.

  • What is the relationship between QD and P as per the law of demand?

    -According to the law of demand, there is a negative relationship between QD (quantity demanded) and P (price), meaning that as price increases, the quantity demanded decreases, and vice versa.

  • How is the inverse demand function derived from the original demand equation?

    -The inverse demand function is derived by isolating P (price) instead of QD (quantity demanded). This involves switching the sides of the equation and dividing each term by the coefficient of P.

  • What is the inverse demand function for the given demand equation?

    -The inverse demand function for the given demand equation is P = 48 - 0.2Q, where P is the price and Q is the quantity demanded.

  • What does the negative coefficient on P in the demand equation signify?

    -The negative coefficient on P signifies the inverse relationship between price and quantity demanded, which is consistent with the law of demand.

  • Why is it recommended to convert fractions to decimals in the inverse demand function if possible?

    -Converting fractions to decimals in the inverse demand function is recommended because many people find it easier to work with finite decimals rather than fractions, especially in economic calculations.

  • What is the significance of functional notation in the context of demand and inverse demand functions?

    -Functional notation, such as Q of P or P of Q, signifies the dependent variable (quantity or price) as a function of the independent variable (price or quantity), clearly indicating the relationship between the two variables.

  • Why is the original demand function typically used for graphing, even though the inverse demand function is also valid?

    -The original demand function is typically used for graphing because it follows the standard convention of having quantity on the x-axis and price on the y-axis, which is more intuitive for visual representation in economics.

  • What does the video suggest for viewers who want to practice understanding demand and inverse demand functions?

    -The video suggests that viewers should practice by taking the original demand function, rearranging it to find the inverse demand function, and vice versa, to solidify their understanding of the concepts.

Outlines
00:00
📚 Introduction to Demand and Inverse Demand Equations

The video script begins with a warm welcome to the channel and an introduction to the topic of the difference between the demand equation and the inverse demand equation. The speaker emphasizes the importance of correctly labeling axes in economic graphs, with price on the y-axis and quantity on the x-axis, to avoid losing marks in assessments. A general demand equation, QD = 240 - 5P, is presented to illustrate the negative relationship between quantity demanded (QD) and price (P), as per the law of demand. The script then introduces the concept of functional notation and the process of deriving the inverse demand function from the original demand equation.

Mindmap
Keywords
💡Demand Curve
The demand curve represents the relationship between the quantity of a good that consumers are willing to buy and its price. In the video, it is described as a downward-sloping curve on a graph with price on the vertical axis and quantity on the horizontal axis, illustrating the law of demand which states that as price increases, quantity demanded decreases.
💡Demand Equation
A demand equation is a mathematical representation of the demand curve, showing how quantity demanded (QD) is related to price (P). The script provides an example of a linear demand equation: QD = 240 - 5P, which demonstrates the negative relationship between price and quantity demanded.
💡Inverse Demand Equation
The inverse demand equation is a rearrangement of the demand equation where price (P) becomes the dependent variable and quantity demanded (QD) is the independent variable. In the script, the original demand equation is transformed into P = 48 - 0.2QD, showing how price can be expressed as a function of quantity demanded.
💡Law of Demand
The law of demand is a fundamental economic principle stating that there is a negative relationship between price and quantity demanded. In the video, this is exemplified by the negative coefficient on the price variable in the demand equation, indicating that as price increases, quantity demanded decreases.
💡Functional Notation
Functional notation is a mathematical way of expressing a function, where one variable is shown as a function of another. In the script, the demand equation is written in functional notation as Q(P) = 240 - 5P, indicating that quantity demanded is a function of price.
💡Dependent and Independent Variables
In the context of functions, a dependent variable is the output that is determined by the input, which is the independent variable. The video explains that in the normal demand function, QD is the dependent variable, and P is the independent variable. In contrast, in the inverse demand function, P becomes the dependent variable, and QD is the independent variable.
💡Linear Equation
A linear equation is an algebraic equation in which the highest power of the variable is one. The script uses a linear demand equation to illustrate the relationship between price and quantity demanded, showing a straight-line relationship on the graph.
💡Algebraic Manipulation
Algebraic manipulation refers to the process of rearranging and transforming equations to solve for different variables. The video demonstrates this by taking the original demand equation and manipulating it to isolate P, resulting in the inverse demand equation.
💡Graphing
Graphing is the process of visually representing data or functions on a coordinate plane. The script mentions that although the original demand equation is solved algebraically, the inverse demand function is what is typically graphed on the demand curve.
💡Economic Principles
Economic principles are fundamental theories that guide the understanding of economic behavior. The video discusses the law of demand as a key economic principle and uses it to explain the relationship between price and quantity demanded.
💡Homework Assignment
A homework assignment is a task given to students to be completed outside of class, often involving practice problems or exercises. The script cautions that mislabeling axes on a graph could result in losing marks on a homework assignment or exam, emphasizing the importance of understanding how to correctly represent economic concepts.
Highlights

Introduction to the difference between the demand equation and the inverse demand equation.

Importance of correctly labeling axes with price on the Y-axis and quantity on the X-axis for the demand curve.

Explanation of the general demand equation QD = 240 - 5P, illustrating the negative relationship between price and quantity demanded.

Clarification on functional notation and the dependent and independent variables in the demand function.

Step-by-step guide on how to derive the inverse demand function from the original demand function.

Switching sides of the equation to isolate P and changing the sign of the coefficient when doing so.

Division of terms to solve for P in the inverse demand function, simplifying the equation.

Conversion of fractions to decimals for ease of use in the inverse demand function.

Final form of the inverse demand function P = 48 - 0.2QD, with functional notation P(Q) = 48 - 0.2Q.

Graphical representation of the demand curve and the inverse demand function on a graph.

Discussion on the general form of a linear equation and its application to the inverse demand function.

Misunderstanding often seen in economics regarding the graphing of the inverse demand function instead of the original.

Advice on practicing the algebraic manipulation of demand functions for better understanding.

Invitation for viewers to engage with the channel by liking, subscribing, and commenting on the video.

Encouragement for viewers to suggest economic topics or homework questions for future video content.

Closing remarks and sign-off for the video, promising to see viewers in the next video.

Transcripts

Browse More Related Video

How to Draw the DEMAND CURVE (Using the DEMAND EQUATION) | Think Econ

Monopoly: Consumer Surplus, Producer Surplus, Deadweight Loss

Linear Demand Equations - part 1

Linear Demand Equations - part 1(NEW 2016)

Ex: Determine a Linear Demand Function

How to Calculate Consumer Surplus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
EconomicsDemand CurveInverse DemandPrice QuantityLaw of DemandLinear EquationFunction NotationAlgebraic SolutionEconomic AnalysisHomework Help