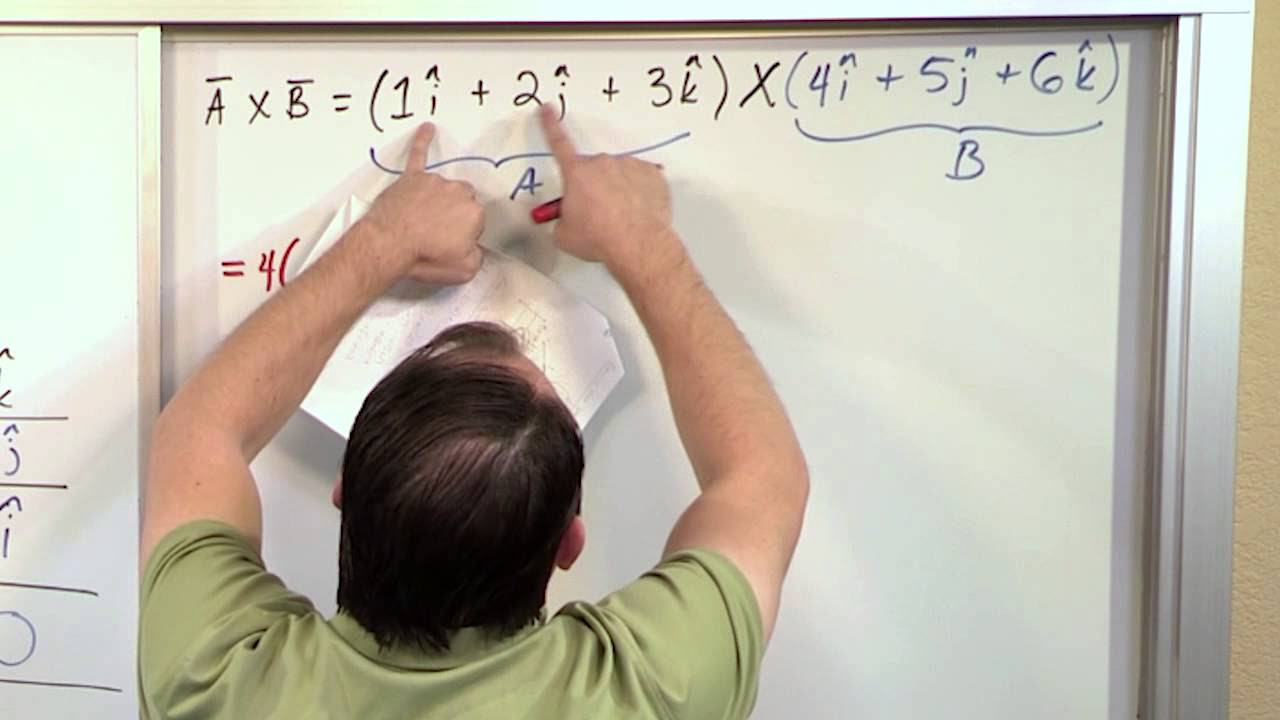Calculus 3: Lecture 11.4 The Cross Product of Two Vectors in Space
TLDRThe video script offers an in-depth exploration of the cross product in vector mathematics, a fundamental concept with broad applications. It explains the cross product's definition, its uniqueness to three-dimensional space, and its calculation using determinants. The script walks through examples, illustrating the process of finding a cross product and converting it into a unit vector orthogonal to two given vectors. It also discusses the physical significance of the cross product, particularly in physics, and introduces a mnemonic technique for quickly determining the cross products of standard unit vectors.
Takeaways
- 📚 The script is a lecture on the concept of the cross product of vectors, emphasizing its importance in various sections of a course.
- 📝 The cross product is defined as a vector operation that is unique to three-dimensional space and does not exist in two or higher dimensions.
- 🧭 The formula for the cross product is introduced using a determinant with the unit vectors i, j, k, and the components of the two vectors involved.
- 📉 The cross product results in a new vector that is perpendicular (orthogonal) to the two original vectors, which is a key property used in physics, such as in calculating torque.
- 🔄 A mnemonic for remembering the cross product calculation is 'plus-minus-plus', which corresponds to the signs of the resulting components.
- 🔢 The determinant method for calculating the cross product involves crossing out rows and columns and computing the remaining submatrices (minors).
- ✅ The script includes an example calculation of the cross product for two given vectors, demonstrating the process step by step.
- 🔄 It is noted that the cross product of a vector with itself results in the zero vector, which can be easily understood from the determinant formula.
- 🔀 The script mentions a property that the cross product of vectors u and v (u cross v) is equal to the negative of the cross product of v and u (-v cross u).
- 📈 The process of finding a unit vector orthogonal to two given vectors is explained, which involves taking their cross product and then normalizing the result.
- 🎯 Finally, the script introduces a visual method for quickly determining the cross products of the standard unit vectors i, j, and k using a cyclic permutation diagram.
Q & A
What is a cross product and why is it significant in vector operations?
-The cross product is a vector operation that takes two vectors in three-dimensional space and results in a new vector that is perpendicular to the original two. It's significant because it's widely used in various fields such as physics and engineering, particularly in calculating torque and the normal vector to a surface.
How is the cross product of two vectors defined mathematically?
-The cross product of two vectors is defined using the determinant of a matrix. The first row of the matrix consists of the unit vectors i, j, k, and the second row consists of the components of the first vector, with the third row containing the components of the second vector.
What is the physical interpretation of the cross product in physics?
-In physics, the cross product is used to find a vector that is perpendicular to two other vectors, which is useful for calculating torque and angular momentum. It also represents the area of a parallelogram spanned by the two vectors.
Why is the cross product unique to three-dimensional space?
-The cross product is unique to three-dimensional space because it requires three orthogonal unit vectors (i, j, k) to be defined. In two dimensions, there are not enough dimensions to define a perpendicular vector, and in higher dimensions, the concept does not naturally extend.
How can you compute the cross product using the determinant method?
-To compute the cross product using the determinant method, you set up a matrix with i, j, k in the first row, the components of the first vector in the second row, and the components of the second vector in the third row. Then, you calculate the determinant by crossing out the row and column of each unit vector and taking the determinant of the remaining submatrix, following the pattern of plus-minus-plus.
What is the geometric interpretation of the cross product result?
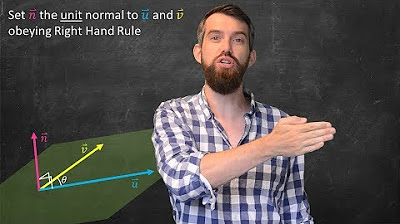
-The geometric interpretation of the cross product result is that it is a vector that is orthogonal to both of the original vectors. Its direction is determined by the right-hand rule, and its magnitude is equal to the area of the parallelogram formed by the two vectors.
What is the relationship between the cross product of a vector with itself and the zero vector?
-The cross product of a vector with itself always results in the zero vector. This is because the determinant of a matrix with two identical rows is zero, and thus the resulting vector has all components equal to zero.
How can you find a unit vector orthogonal to two given vectors?
-To find a unit vector orthogonal to two given vectors, first compute the cross product of the two vectors to get a vector orthogonal to both. Then, normalize this resulting vector by dividing it by its magnitude to get a unit vector.
What is the significance of the right-hand rule in the context of the cross product?
-The right-hand rule is a common mnemonic used to determine the direction of the cross product vector. If you point your index finger in the direction of the first vector and your middle finger in the direction of the second vector, your thumb will point in the direction of the cross product vector.
Can you provide an example of a practical application of the cross product in physics?
-In physics, the cross product is used to calculate torque, which is the rotational force applied to an object. The torque is the cross product of the position vector from the pivot point to the point of force application and the force vector itself.
Outlines
📚 Introduction to Cross Product in Vectors
The script begins with an introduction to the cross product of vectors, a fundamental concept in vector mathematics. The instructor explains the cross product as a vector operation that is prevalent throughout various sections of the course. The definition of the cross product is given, and the instructor demonstrates how to represent vectors in ijk form, which is a linear combination of the unit vectors i, j, and k. The importance of the cross product in three-dimensional space is emphasized, as it is unique to 3D and does not have an equivalent in two or higher dimensions. The formula for the cross product is introduced using a determinant and a matrix, with the instructor providing a method to memorize the formula by aligning the vectors' components in a 3x3 matrix and following a specific pattern of signs to compute the result.
🔍 Calculating the Cross Product Using Determinants
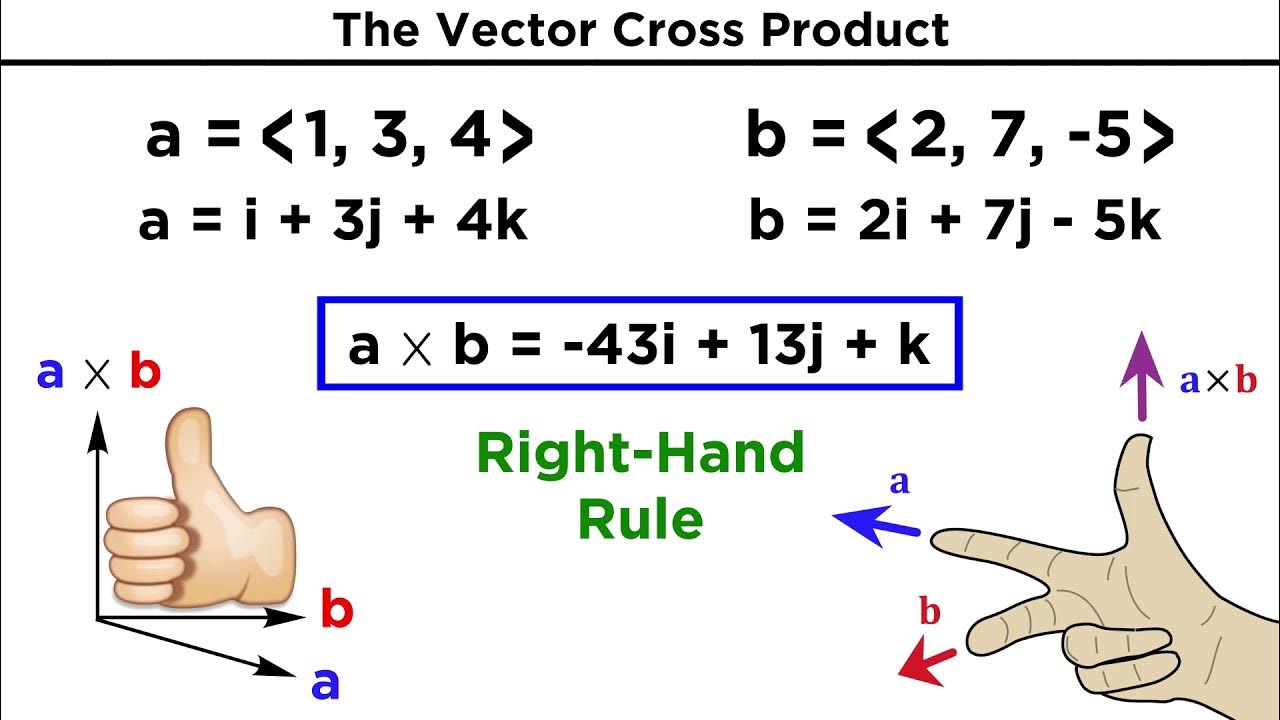
The paragraph delves deeper into the mechanics of calculating the cross product by using determinants. The process involves creating a matrix with the unit vectors i, j, k and the components of two given vectors, then applying a cross-out method to find the determinant of the remaining sub-matrix for each component of the resulting vector. The instructor also contrasts the method used in calculus with that in linear algebra, highlighting the cofactor expansion technique in linear algebra. The summary includes an example problem where two vectors are given, and the cross product is calculated step by step, emphasizing the importance of memorizing the plus-minus-plus pattern for the calculation.
📘 Further Exploration of Cross Product Computation
This section continues the exploration of the cross product, emphasizing the importance of accurate computation and the common mistakes made by students. The instructor provides a detailed example of calculating the cross product of two vectors, highlighting the steps and the arithmetic involved. The explanation includes a brief discussion on the notation used in matrices and determinants, pointing out the common practice of omitting parentheses for simplicity. The paragraph concludes with the instructor's personal anecdotes about student mistakes and the importance of getting the calculation right to avoid grading issues.
🚀 Understanding the Cross Product's Resultant Vector
The focus shifts to understanding the properties of the resultant vector from the cross product. The instructor explains that the cross product yields a vector that is perpendicular to the original two vectors, a concept that is fundamental in physics, particularly in statics and torque calculations. The summary includes an example where the cross product of two vectors is computed, and the resulting vector is shown to be orthogonal to both original vectors. The instructor also introduces a shortcut for calculating the cross product when the order of the vectors is reversed, simplifying the process by just flipping the signs of the components.
🎯 Cross Product's Orthogonality and Uniqueness to 3D
The script emphasizes the orthogonality of the cross product, which is a vector that is perpendicular to the two original vectors involved in the operation. It also reiterates that the cross product is unique to three-dimensional space and does not exist in two or higher dimensions. The instructor provides a homework problem involving two vectors and asks students to find the cross product, encouraging collaboration and the use of calculators for computation. The paragraph concludes with a discussion about the practicality of the cross product in physics and its applications.
📝 Practical Application of Cross Product in Physics
The instructor discusses the practical applications of the cross product in physics, particularly in the context of torque and statics. The explanation includes an example of finding the cross product of two vectors, with the instructor guiding the students through the calculation process. The importance of the cross product in determining orthogonality is highlighted, and the instructor uses humor to engage the students in the learning process. The paragraph concludes with a brief mention of a homework problem and the importance of understanding the cross product for future sections of the course.
🔄 The Relationship Between Dot Product and Cross Product
This section explores the relationship between the dot product and the cross product, highlighting the differences between the two operations. The dot product results in a scalar value that can indicate orthogonality if the result is zero, whereas the cross product yields a vector that is perpendicular to the original vectors. The instructor uses an example to illustrate this concept and discusses the implications of taking the cross product of a vector with itself, which always results in the zero vector. The paragraph concludes with a discussion on the importance of understanding these vector operations for exams and further studies.
🧭 Finding Orthogonal Unit Vectors Using Cross Products
The script introduces a method for finding a unit vector that is orthogonal to two given vectors. The process involves first calculating the cross product of the two vectors to find a vector that is perpendicular to both, and then normalizing this vector to have a magnitude of one, thus creating a unit vector. The instructor provides a step-by-step example, including the calculation of the cross product and the subsequent normalization. The importance of this technique is emphasized, as it is a common problem type in exams and homework assignments.
🎨 Visualizing Cross Products with Unit Vectors
The instructor presents a visual method for computing cross products using standard unit vectors i, j, and k. This method involves following the arrows on a diagram of the unit vectors to determine the result of the cross product, with the direction indicated by the arrows and the sign determined by the order of the vectors. The paragraph includes several examples of cross products between unit vectors, demonstrating how this technique can simplify calculations and provide a quick way to determine the result of common cross product operations.
🗂 Wrapping Up and Transitioning to the Next Section
The script concludes with a summary of the cross product concepts covered and a transition to the next section of the course. The instructor reflects on the importance of the cross product in various applications, including physics, and the utility of the visual method for computing cross products with unit vectors. The paragraph ends with a light-hearted discussion about the potential inclusion of cross product problems on exams, emphasizing the importance of understanding the material for future assessments.
Mindmap
Keywords
💡Cross Product
💡Vector
💡Determinant
💡Orthogonal
💡Unit Vector
💡Component Form
💡I, J, K Notation
💡Minor
💡Cofactor Expansion
💡Perpendicular
Highlights
Introduction to the cross product of vectors, a fundamental operation in vector calculus.
The cross product is unique to three-dimensional space and does not exist in higher dimensions.
The definition of the cross product using the determinant and the i, j, k unit vectors.
The cross product formula memorization technique using a matrix with i, j, k and vector components.
Calculation of the cross product using the determinant of a matrix with specific row and column elimination.
The cross product result is a vector orthogonal to the original vectors, with practical applications in physics.
The cross product's property of being unchanged when switching the order of the vectors, except for a sign change.
Illustration of the cross product calculation between two example vectors.
Explanation of the physical meaning of the cross product in terms of torque in physics.
The cross product's limitation to three-dimensional vectors and its non-applicability in other dimensions.
Demonstration of the cross product calculation for a homework problem involving vectors in component form.
The importance of the cross product in various sections of a calculus course and its relevance in future studies.
The concept of normalizing a vector to find a unit vector orthogonal to two given vectors.
A method to visualize and compute cross products using standard unit vectors in a circular arrangement.
The cross product's utility in determining perpendicularity and its difference from the dot product.
A unique approach to finding cross products using a circular diagram of unit vectors.
The potential inclusion of cross product problems in an exam, emphasizing their importance in the course.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: