Physics 15 Torque (1 of 27) Boom and Guy Wire
TLDRThis video script presents a detailed analysis of the forces and torques acting on a boom, specifically focusing on a guy wire tension scenario. The problem assumes a static situation with no friction at the pivot point, allowing the boom to rotate freely. The goal is to determine the force in the X and Y directions on the boom, as well as the total force and its direction relative to the boom. The solution involves applying the principles of static equilibrium, where the sum of forces in both X and Y directions and the sum of torques equal zero. By calculating the distances from the forces' lines of action to the pivot point, and using the known weights and angles, the script derives the tension in the guy wire, the forces acting on the boom, and the angle at which the total force acts. The final calculation reveals a tension of 1347 Newtons in the guy wire and a total force acting at approximately 75 degrees to the boom, illustrating a practical application of statics in engineering.
Takeaways
- 🔍 **Static Equilibrium**: The problem assumes a static situation where the sum of all forces and torques equals zero, as nothing is moving.
- ⚖️ **Forces in X and Y Directions**: The goal is to find the force in the X and Y directions acting on the boom, assuming no friction at the pivot point.
- 📐 **Torque Calculation**: Torques are calculated around a chosen pivot point, with counterclockwise torque considered positive and clockwise negative.
- 📏 **Distances and Angles**: Distances from the line of action of forces to the pivot point (D1, D2, D3) and angles (60 degrees and 30 degrees) are crucial for torque calculations.
- 🔢 **Force and Distance Product**: The product of force and distance from the pivot point is used to calculate the torque for each force acting on the boom.
- 🧭 **Tension in the Guy Wire**: The tension in the guy wire is found by solving the torque equation, which involves the cosine of 30 and 60 degrees.
- 📍 **Forces on the Boom**: After finding the tension, the forces in the X and Y directions on the boom are determined by summing these forces to zero.
- 📐 **Angle of Total Force**: The angle at which the total force acts on the boom is found using the arctangent function of the ratio of vertical to horizontal force components.
- 📈 **Calculation of Tension**: The tension in the guy wire is calculated to be 1347 Newtons after solving the equilibrium equations.
- 📊 **Resulting Forces**: The force in the X direction (F_X) is found to be 1347 Newtons, and the force in the Y direction (F_Y) is 5000 Newtons.
- 🔍 **Angle Verification**: The angle of the total force acting on the boom is verified to be approximately 75 degrees, not 60 degrees as initially estimated.
Q & A
What is the main objective of the example problem?
-The main objective is to find the tension in the guy wire, the force on the boom in both the X and Y directions, and the total force's direction relative to the boom.
What are the three principles used to solve the problem?
-The three principles are the sum of all forces in the x-direction equals zero, the sum of all forces in the y-direction equals zero, and the sum of all torques equals zero.
What is the convention for torque direction in this problem?
-The convention is that any torque in the counterclockwise direction is positive, and any torque in the clockwise direction is negative.
How many torques are there contributing to the problem?
-There are three torques contributing to the problem: one caused by the weight hanging down from the boom, one by the weight of the beam, and the third by the tension in the guy wire.
What are the symbols used to represent the distances from the forces to the pivot point?
-The symbols used are D1, D2, and D3, representing the distances from the line of action of the respective forces to the pivot point.
What is the method to find the distances D1, D2, and D3?
-The distances are found using trigonometric relationships based on the angles and the length of the beam (L), applying cosine for adjacent sides and sine for opposite sides.
What is the final calculated tension in the guy wire?
-The final calculated tension in the guy wire is 1347 Newtons.
How are the forces in the X and Y directions on the boom determined?
-The forces in the X and Y directions are determined by setting up equations where the sum of forces in each direction equals zero and solving for the unknown forces.
What is the angle at which the total force acts on the boom?
-The angle at which the total force acts on the boom is approximately 75 degrees.
Why is it important to find the angle of the total force acting on the boom?
-Finding the angle is important to understand the direction of the resultant force and how it affects the boom, which can indicate potential structural integrity issues or necessary adjustments.
How does the example problem demonstrate the application of statics in real-world scenarios?
-The problem demonstrates the application of statics by analyzing the forces and torques acting on a boom and guy wire system, which is a common structure in engineering and construction for supporting heavy loads.
What is the significance of using the cosine and sine functions in this problem?
-The cosine and sine functions are used to relate the forces and distances in the problem to the angles formed, allowing for the calculation of unknown distances and forces based on the geometry of the system.
Outlines
🔍 Static Equilibrium Analysis of a Boom and Guy Wire System
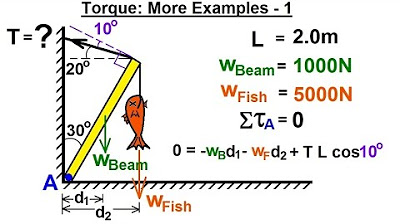
This paragraph introduces a physics problem involving a boom and a guy wire. The goal is to calculate the tension in the guy wire and the forces acting on the boom in both the X and Y directions. The problem assumes no friction at the pivot point and uses principles of static equilibrium, where the sum of forces and torques equals zero. The process involves calculating torques caused by the weight at the end of the boom, the weight of the beam itself, and the tension in the guy wire. The distances from the pivot point to the lines of action of these forces (D1, D2, and D3) are determined using trigonometric relationships, and the problem concludes with setting up equations to solve for the unknowns.
📐 Trigonometric Calculations for Torque and Tension
The second paragraph delves into the trigonometric calculations necessary to find the distances (D1, D2, D3) and subsequently the tension in the guy wire. It explains how to use the cosine of 60 and 30 degrees to express these distances in terms of the boom's length (L). The paragraph walks through the process of summing torques around a pivot point and solving for the tension (T) in the guy wire. It also calculates the forces acting on the boom in the X and Y directions, using the equilibrium condition that the sum of forces in each direction equals zero. The paragraph concludes with the calculation of the resultant force's direction, using the arctangent function to find the angle of the combined forces acting on the boom.
🔧 Summary of Forces and Torques in a Static Boom System
The final paragraph summarizes the process of analyzing the boom and guy wire system. It emphasizes the importance of summing torques around a pivot point to find the unknown forces and tensions. The paragraph reiterates the steps taken to calculate the forces acting on the boom in both horizontal and vertical directions and how these forces combine to create a resultant force at a specific angle to the boom. It concludes by highlighting that the force does not act along the boom but at an angle, which is a common outcome in such static equilibrium problems.
Mindmap
Keywords
💡Tension
💡Static Equilibrium
💡Force in X and Y Direction
💡Torque
💡Frictionless
💡Pivot Point
💡Distance (D1, D2, D3)
💡Cosine and Sine
💡Arc Tangent (arctan)
💡Boom
💡Counterclockwise and Clockwise
Highlights
The problem involves finding the tension in a guy wire and the forces on a boom in a static situation.
Assumptions include no friction at the pivot point and that the boom can rotate freely.
The approach uses principles of statics, where the sum of forces and torques equals zero.
Torque convention is set with counterclockwise being positive and clockwise being negative.
The sum of all torques relative to a chosen pivot point is set to zero to find unknowns.
Distances from lines of action of forces to the pivot point are denoted as D1, D2, and D3.
D1 is calculated using the cosine of 60 degrees, assuming the length of the beam (L) will cancel out.
D2 is found by considering the center of mass of the beam located 1/3 from the bottom.
D3 is determined by the cosine of 30 degrees, representing the distance from the guy wire's tension to the pivot.
The tension in the guy wire (T) is solved by isolating it in the torque equation.
The force acting on the boom in the X direction (F sub X) is found by balancing the tension with an opposing force.
The force in the Y direction is the sum of the weight forces acting on the boom and the weight hanging from it.
The total force on the boom is found by combining the X and Y components.
The angle of the total force relative to the boom is determined using the arctangent function.
The angle of the total force is found to be approximately 75 degrees, not aligned with the boom.
The problem demonstrates how to analyze forces and torques in a static system using trigonometric functions.
The solution process emphasizes the importance of correctly identifying and calculating distances and angles.
The final answer for the tension in the guy wire is 1347 Newtons.
The force analysis shows that the boom experiences a force at an angle, not along its length.
Transcripts
Browse More Related Video
Physics 15 Torque Example 2 (2 of 7) Mass on Rod and Cable

Physics 15 Torque Example 4 (4 of 7) The Diving Board
Physics 15 Torque (5 of 27) Tension=? Supporting a Gate
Physics 15 Torque (23 of 25) More Examples: 5 F(A)=? F(B)=? of Simple Truss
Physics 15 Torque Example 3 (3 of 7) Mass on Rod and Cable
Physics 15 Torque (19 of 25) More Examples: 1 T=? of Cable Holding Fish
5.0 / 5 (0 votes)
Thanks for rating: