Physics 15 Torque Example 4 (4 of 7) The Diving Board

Michel van Biezen
7 Apr 201309:00
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a detailed explanation of how to calculate the forces exerted on the supports of a diving board using the concept of torque. The scenario involves a diver standing at the end of the board, which is supported at two points. The problem-solving approach involves selecting a pivot point and applying the equation that the sum of all torques equals zero. The script guides through identifying the forces acting on the board, such as the diver's weight, the board's weight, and the reaction forces at the supports. It then calculates the distances from the pivot point to the lines of action of these forces, which are crucial for the torque calculations. The process involves finding the force on the first support (F1) by setting up an equation based on torques and solving for the unknown force. Subsequently, the force on the second support (F2) is determined by ensuring the sum of forces in the vertical direction equals zero, considering the weights of the diver and the board along with the found force F1. The final step includes plugging in the values for the weights and gravitational acceleration to find the forces in Newtons. This methodical approach provides a clear understanding of torque and its application in real-world scenarios.

Takeaways
  • 🧮 To solve for the forces on the supports of a diving board, we use the equation that the sum of all torques equals zero.
  • 🏊‍♂️ The weight of the diver at the end of the diving board creates a torque that needs to be balanced by the forces at the supports.
  • ⚖️ A pivot point is chosen to calculate the torques; it can be anywhere on the board, but the script chooses the board's supported points as pivot points.
  • 📐 The distances from the pivot point to the line of action of the forces (D1, D2, D3) are crucial for torque calculations.
  • 📏 Distance one (D1) is the distance from the diver's end to the chosen pivot point, which is given as 3 meters.
  • 🎢 The center of mass for the board is at the halfway point of its length, hence D2 is half the board's length minus the distance from the diver to the pivot point.
  • 🤸‍♀️ The force at support one (F1) prevents the board from tipping upwards and is calculated using the perpendicular distance to the pivot point (D3).
  • 📉 The sum of the forces in the vertical direction must equal zero, which helps in finding the force on support two (F2).
  • 🔢 The mass of the diver (small m) and the board (big M), along with the acceleration due to gravity (g), are used to calculate the forces in newtons.
  • 🧷 The force exerted on support one (F1) is found to be 735 newtons after substituting the given values into the torque equation.
  • ⏏️ The force on support two (F2) is determined by summing the weight of the board, the weight of the diver, and the force F1, resulting in 1715 newtons acting upwards.
  • 🔄 The process demonstrates the application of torque and force equilibrium concepts in a real-world scenario, specifically in the context of a diving board.
Q & A

  • What is the primary focus of the example discussed in the transcript?

    -The primary focus is on calculating the forces exerted on the two supports of a diving board.

  • What is the equation used to find the forces on the supports?

    -The equation is based on the principle that the sum of all torques (torquing actions) around a pivot point equals zero.

  • Why is it necessary to choose a pivot point?

    -A pivot point is necessary to calculate the torques exerted by the forces acting on the diving board, as torque is a measure of the force acting at a distance from the pivot point.

  • What are the three forces considered in the problem?

    -The three forces are the weight of the diver (mg), the weight of the board (Big mg), and the force exerted by support one (F1).

  • How is the center of mass of the board determined?

    -The center of mass of the board is determined to be at the halfway point of the board's length.

  • What is the significance of the perpendicular distance in calculating torque?

    -The perpendicular distance from the pivot point to the line of action of the force is crucial in calculating torque, as torque is the product of the force and the perpendicular distance.

  • What is the direction assigned to positive and negative torques in this problem?

    -Clockwise torque is considered positive, and counterclockwise torque is considered negative.

  • What is the final calculated force on support one (F1) in Newtons?

    -The final calculated force on support one (F1) is 735 Newtons.

  • How is the force on support two (F2) determined?

    -The force on support two (F2) is determined by considering the sum of all forces in the y-direction to be zero and solving for F2.

  • What is the total force on the second pivot point?

    -The total force on the second pivot point is 1715 Newtons, acting upward.

  • Why is it important to consider the units when performing the calculations?

    -Considering the units is important to ensure that the final answer is expressed in the correct units of force, which are Newtons in this context.

  • What is the role of the support one (F1) in preventing the board from tipping?

    -Support one (F1) provides a downward force that counteracts the tipping effect caused by the weight of the diver and the board, ensuring the board remains horizontal.

Outlines
00:00
🧮 Calculating Torque on a Diving Board

The first paragraph introduces a physics problem involving a diving board and the forces acting upon it. It describes the scenario where a diver's weight is creating a torque on the board, which is supported at two points. The goal is to find the forces on the two supports. To solve this, the script uses the equation that the sum of all torques equals zero, selecting a pivot point and calculating the torques created by the diver's weight, the board's weight, and the force exerted by support one. The distances from the pivot point to the lines of action for each force are identified as D1, D2, and D3. The problem concludes with the setup for calculating the force on support one (F1) using the known distances and the weights of the diver (small m) and the board (Big M).

05:01
📐 Solving for Support Forces and Torque

The second paragraph continues the physics problem by calculating the force on the first support (F1). It outlines the process of summing forces in the y-direction to zero, including the force F1, the weights of the diver (small mg) and the board (Big mg), and the upward force F2. By rearranging the forces and substituting known values, the paragraph concludes with the calculation of F1 as 735 Newtons. It then proceeds to find the force on the second support (F2) by considering the balance of forces acting on the board. The final calculation results in F2 being 1715 Newtons, which acts upward, thus solving the torque problem for the diving board scenario.

Mindmap
Keywords
💡Torque
Torque is the rotational equivalent of linear force. It is a measure of the force that can cause an object to rotate around an axis. In the video, torque is used to analyze the forces acting on a diving board and how they affect the board's rotation, with the sum of all torques equaling zero.
💡Diving Board
A diving board is a structure used in diving sports to allow divers to dive from a height. In the context of the video, it serves as an example to illustrate the principles of torque, with the board being subjected to various forces that cause it to rotate around its supports.
💡Pivot Point
The pivot point is the point around which an object rotates. In the video, the pivot point is chosen to calculate the torques acting on the diving board. The choice of pivot point is crucial for the correct application of the torque equation.
💡Force
Force is a physical quantity that represents the interaction between objects, causing a change in motion. In the video, different forces such as the weight of the diver, the weight of the board, and the forces exerted by the supports are considered to calculate the torques and the resulting forces on the supports.
💡Center of Mass
The center of mass is the point at which the mass of an object is concentrated for the purpose of analyzing its motion. In the video, the center of mass of the diving board is identified as the halfway point along its length, which is important for determining the location of the weight of the board acting due to gravity.
💡Distance
Distance in this context refers to the perpendicular distance from the pivot point to the line of action of a force. It is used in the calculation of torque. In the video, various distances (D1, D2, D3) are measured to determine the torques due to the diver's weight, the board's weight, and the support forces.
💡Sum of Torques
The sum of torques is a principle stating that in a system in equilibrium, the total of all torques equals zero. This is used in the video to set up an equation to solve for the unknown forces on the diving board's supports.
💡Equilibrium
Equilibrium refers to a state in which all forces and torques are balanced, resulting in no net force or torque. The video discusses how the diving board is in equilibrium under the action of various forces, which is why the sum of torques around a pivot point is zero.
💡Support Forces
Support forces are the forces exerted by supports to counteract other forces acting on an object. In the video, the forces on support one and support two are the unknowns that need to be found. These forces are crucial in maintaining the diving board's equilibrium.
💡Direction of Forces
The direction of forces is important in determining whether a force contributes to a positive or negative torque. In the video, forces are categorized as acting in a clockwise (positive) or counterclockwise (negative) direction, which affects how they are included in the torque equation.
💡Newtons
Newtons are the unit of force in the International System of Units (SI). In the video, the force exerted on the supports is calculated in Newtons, which is the standard unit for expressing force and is used to quantify the support forces acting on the diving board.
Highlights

Introduction to the concept of torque and its application to a diving board scenario.

Explanation of the forces acting on a diving board due to the diver's weight and the board's own mass.

Use of the equation that the sum of all torques equals zero to solve for the forces on the supports.

Selection of a pivot point to analyze the torque around it.

Identification of three forces acting on the diving board: diver's weight, board's weight, and support force.

Calculation of distances from the pivot point to the lines of action of the forces.

Writing the torque equation by summing up the products of forces and their respective distances.

Determination of distances D1, D2, and D3 based on the board's dimensions.

Isolation of the variable F1 (force on support one) to find its value.

Substitution of known values into the equation to calculate F1.

Conversion of units from meters to Newtons to find the force in the correct units.

Calculation of F1 resulting in a force of 735 Newtons.

Method to find the force on the second support by considering the sum of forces in the y-direction.

Setting up an equation to solve for F2 (force on support two) using the forces acting on the board.

Summation of all forces acting on the board to find the upward force F2.

Substitution of values and calculation resulting in F2 being 1715 Newtons.

Practical application of torque principles to a real-world problem, illustrating the balance of forces.

Demonstration of how to approach and solve complex torque problems using systematic methods.

Transcripts

Browse More Related Video

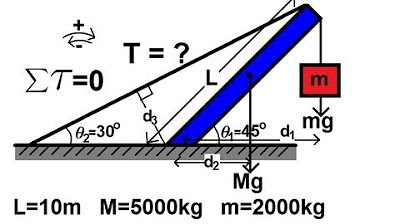
Physics 15 Torque Example 3 (3 of 7) Mass on Rod and Cable

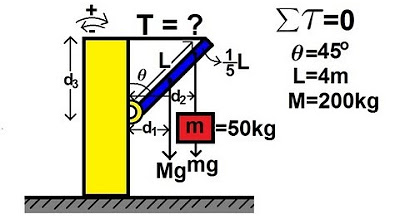
Physics 15 Torque Example 2 (2 of 7) Mass on Rod and Cable

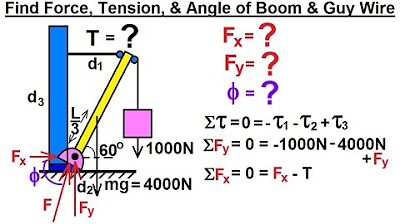
Physics 15 Torque (1 of 27) Boom and Guy Wire

Static Equilibrium: concept

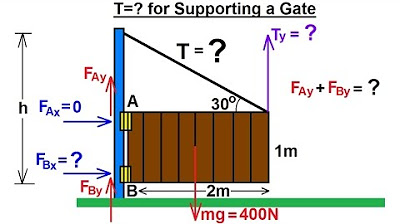
Physics 15 Torque (5 of 27) Tension=? Supporting a Gate

Physics 15 Torque (23 of 25) More Examples: 5 F(A)=? F(B)=? of Simple Truss

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Torque CalculationPhysics ExampleDiving BoardForce AnalysisEquilibriumEngineering MechanicsProblem SolvingEducational ContentScience TutorialMathematical ApproachNewton's Laws