Physics 15 Torque Example 2 (2 of 7) Mass on Rod and Cable

Michel van Biezen
3 Apr 201308:55
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a detailed walkthrough of solving a static torque problem. The lecturer begins by establishing that in a static problem, the sum of all forces and torques equals zero. A pivot point is chosen, and the forces acting on the system are identified: the weight of a hanging mass (mg), the weight of the beam itself (big mg), and the tension in a cable. The corresponding torques for each force are calculated based on their distances from the pivot point. The distances (d1, d2, d3) are determined using trigonometric relationships with the beam's length (L) and angles. The problem is solved algebraically by setting the sum of torques to zero and solving for the unknown tension (T) in the cable. The final answer is obtained by substituting known values and using the tangent of a 45-degree angle, resulting in a cable tension of 1372 Newtons. The summary emphasizes the importance of correctly identifying forces and torques, applying trigonometry to find distances, and performing algebraic manipulations to solve for the unknown.

Takeaways
  • 📚 The problem is a statics problem, meaning no movement or acceleration is involved.
  • ⚖️ The sum of all forces and torques acting on the system must be zero.
  • 🔴 Clockwise torque is considered positive, and counterclockwise torque is negative.
  • 📐 The torque for each force is calculated as the force multiplied by the perpendicular distance from the pivot point to the line of action of the force.
  • 📐 The distances (d1, d2, d3) are crucial to determining the torques and are found using trigonometry based on the geometry of the problem.
  • 🧮 The equation for the sum of torques is set to zero, and solved step by step.
  • 🔢 The distances are expressed in terms of the beam's length (L) and the angle (theta) using trigonometric functions.
  • 📐 The triangle formed by the beam and the forces helps in finding the distances to the line of action of each force.
  • ➗ The length of the beam (L) can be canceled out from the equation since it's a common factor in every term.
  • 🔄 The final equation is rearranged to solve for the tension (T) in the cable, involving the mass (M), gravitational acceleration (g), and the tangent of the angle (theta).
  • 📝 The values for the mass of the hanging object, the mass of the beam, and the gravitational acceleration are substituted into the equation to find the numerical solution for the tension.
  • 📊 The tangent of 45 degrees is equal to 1, simplifying the final calculation.
Q & A

  • What is the main principle used to solve the torque problem in the given script?

    -The main principle used is that the sum of all the torques about a chosen pivot point must add up to zero in a static problem where the sum of all forces is also zero.

  • How are torques defined in the context of the problem?

    -Torques are defined as the product of a force and the perpendicular distance from the pivot point to the line of action of that force. Clockwise torque is considered positive, and counterclockwise torque is considered negative.

  • What are the three forces acting on the beam in the problem?

    -The three forces acting on the beam are the weight of the hanging mass (mg), the weight of the beam itself (big mg), and the tension in the cable.

  • How is the distance associated with each force calculated in the problem?

    -The distances associated with each force (d1, d2, d3) are calculated by drawing triangles and using trigonometric relationships, such as sine and cosine, based on the angles and the length of the beam.

  • What is the significance of the angle theta in the problem?

    -The angle theta is significant because it is used to calculate the distances d1, d2, and d3 using trigonometric functions (sine and cosine), which are then used to compute the torques and solve the problem.

  • How does the lecturer approach the problem algebraically?

    -The lecturer first sets up the equation with the torques (T1, T2, T3) and identifies the distances (d1, d2, d3). After finding the distances, the lecturer cancels out the common length L from the equation and then divides both sides by the cosine of theta to solve for the tension T in the cable.

  • What is the final calculated tension in the cable?

    -The final calculated tension in the cable is 1372 Newtons.

  • Why is it important to identify and label the distances (d1, d2, d3) from the pivot point to the line of action of each force?

    -Identifying and labeling the distances is important because it helps in setting up the correct equation for the torques and ensures that the perpendicular distances are accurately represented in the calculations.

  • What is the role of trigonometry in solving this torque problem?

    -Trigonometry plays a crucial role in calculating the distances from the pivot point to the line of action of the forces, which are necessary to compute the torques. Specifically, sine and cosine functions are used to relate the angles and sides of the triangles formed by the forces and the beam.

  • How does the lecturer ensure that the correct equation is written on the board?

    -The lecturer ensures this by first writing the equation for the torques (T1, T2, T3) and then identifying the distances (d1, d2, d3) one by one. The讲师逐步计算每个距离，并确保它们在图形上正确标记，然后将其插入方程中，最后通过代数操作解决问题。

  • What is the significance of the tangent of 45 degrees in the final calculation?

    -The tangent of 45 degrees is significant because it equals 1, which simplifies the final calculation of the tension in the cable. This is a result of the specific angle theta being 45 degrees, which is a common scenario in many statics problems.

  • Why is it necessary to draw triangles when calculating the distances associated with the forces?

    -Drawing triangles is necessary because it helps visualize and apply trigonometric principles to find the perpendicular distances from the pivot point to the line of action of each force. These distances are essential for calculating the torques.

  • How does the lecturer ensure that the algebraic manipulation of the equation is done correctly?

    -The lecturer ensures this by systematically identifying each torque, calculating the associated distances, and then carefully performing algebraic operations, such as canceling out common terms and dividing by the cosine of theta, to isolate and solve for the unknown tension in the cable.

Outlines
00:00
🔍 Static Torque Problem Analysis

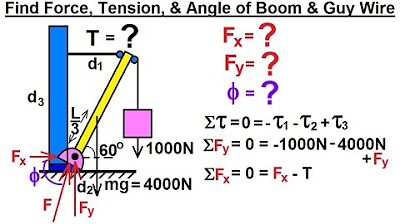
The paragraph introduces a static torque problem where the sum of all forces and torques equals zero. The lecturer chooses a pivot point and identifies three forces acting on a beam: the weight of a hanging mass (mg), the weight of the beam itself (big mg), and the tension in a cable. The concept of torque is explained, with clockwise torque considered positive and counterclockwise negative. The distances from the forces' lines of action to the pivot point (d1, d2, d3) are identified as crucial for calculating torques. The problem is approached step by step, starting with defining the forces and their distances, and then calculating the torques around the chosen pivot point.

05:00
📐 Calculating Distances and Solving the Torque Equation

This paragraph delves into calculating the distances (d1, d2, d3) from the forces' lines of action to the pivot point using trigonometric relationships in triangles formed by the beam and the forces. The讲师 (lecturer) uses the sine function to find d1, which is opposite an angle theta in a triangle where the adjacent side is 4/5 the length of the beam (L). For d2, the lecturer uses the sine of the angle theta again, but with the hypotenuse being half the length of the beam (L/2). The distance d3 is found using the cosine of the angle theta, as it is adjacent to the angle. After establishing the distances, the lecturer simplifies the torque equation by canceling out the common factor L and rearranging the terms to solve for the tension in the cable (T). The final step involves substituting the given values for the masses and gravitational acceleration to calculate the tension in the cable, which is found to be 1372 Newtons after using a calculator.

Mindmap
Keywords
💡Torque
Torque is the rotational equivalent of linear force. It is a measure of the force that can cause an object to rotate about an axis. In the video, torque is central to solving the statics problem, as the sum of all torques about a chosen pivot point must be zero. The script describes how to calculate the torque caused by different forces acting on a beam, such as the weight of a hanging mass (mg) and the tension in a cable.
💡Static Problem
A static problem refers to a scenario where no objects are moving or accelerating. The forces and torques in such a situation are balanced, resulting in a net force and net torque of zero. The video script uses this concept to analyze the forces and their respective torques acting on a beam in a stationary state.
💡Pivot Point
The pivot point is the point around which the torques are calculated. It is an essential concept in the video as it is the reference point for determining the distances associated with each force, which are then used to calculate the torques. The script specifies a pivot point and uses it to pivot everything for the problem-solving process.
💡Forces Acting
In the context of the video, forces acting refers to the different forces that influence the motion or state of equilibrium of an object. The script identifies three forces acting on the beam: the weight of the hanging mass (mg), the weight of the beam itself (big mg), and the tension in the cable. These forces are then used to calculate the torques around the pivot point.
💡Distance to Line of Action
This refers to the perpendicular distance from the pivot point to the line of action of a force. In the video, this distance is critical for calculating the torque because torque is the product of the force and the distance to its line of action. The script describes how to determine these distances (d1, d2, d3) for each force acting on the beam.
💡Tension in the Cable
Tension in the cable refers to the force exerted by a cable when it is taut and pulling on an object. In the script, the tension force is one of the three forces considered in the torque problem. The tension force is analyzed for its effect on the beam's rotation and its contribution to the total torque around the pivot point.
💡Clockwise and Counterclockwise Torque
The video script defines clockwise torque as positive and counterclockwise torque as negative. This convention is used to establish the direction of the torque, which is important when calculating the net torque in a system. The script uses this definition to determine the sign of the torque caused by each force acting on the beam.
💡Sum of Torques
The sum of torques is a principle used in statics that states the total torque acting on an object in equilibrium is zero. This principle is fundamental to the problem-solving process described in the video. The script uses this principle to set up an equation that relates the torques caused by the different forces to solve for the unknown tension in the cable.
💡Trigonometric Functions
Trigonometric functions, such as sine and cosine, are used in the video to relate the distances (d1, d2, d3) to the angles in the problem. These functions are essential for calculating the distances to the line of action of the forces, which are then used to compute the torques. The script uses the sine of an angle (theta) to find distances d1 and d2 and the cosine of the angle for distance d3.
💡Equation of Statics
The equation of statics is used to express the condition of equilibrium for an object under the action of several forces. In the video, the equation is set up to represent the sum of all torques equaling zero. This equation is then solved for the unknown variables, such as the tension in the cable, using the known values and trigonometric relationships.
💡Mass and Weight
Mass is the measure of the amount of matter in an object, while weight is the force exerted by gravity on that mass. In the video, the weight of the hanging mass (mg) and the weight of the beam (big mg) are identified as forces that contribute to the torques acting on the beam. These weights are calculated based on the given masses (50 kg for the hanging mass and 200 kg for the beam) and the acceleration due to gravity (9.8 m/s²).
Highlights

The lecture introduces a static torque problem where the sum of all forces and torques is zero.

The concept of summing torques about a chosen pivot point to zero is used to solve the problem.

Identifying forces acting on the problem is the first step, including the weight of the mass and the beam, and the tension in the cable.

Torque is calculated as the product of force and the perpendicular distance from the pivot point to the line of action of the force.

Clockwise torque is defined as positive and counterclockwise as negative in the context of this problem.

The distance associated with each force (d1, d2, d3) is calculated using trigonometric relationships based on the geometry of the problem.

The triangle formed by the beam and the forces is used to determine distances d1, d2, and d3.

Angles within the triangles are used to apply trigonometric functions (sine and cosine) to find the distances.

The sum of the torques equation is set up with the identified forces and their respective distances.

The length of the beam (L) is factored out from the equation as a common factor.

The tension in the cable (T) is solved by rearranging the torque equation and applying trigonometric identities.

The tangent of the angle (theta) is used to simplify the equation, which equals 1 for a 45-degree angle.

The numerical values for the mass of the hanging object (50 kg) and the beam (200 kg) are used to calculate the tension.

The acceleration due to gravity (g = 9.8 m/s²) is included in the final calculation of the tension.

The final answer for the tension in the cable is derived using algebraic manipulation and substitution of known values.

The lecture emphasizes the importance of correctly setting up the equation and using algebra to solve for the unknowns.

A step-by-step approach is recommended to avoid confusion and ensure the accuracy of the final solution.

Transcripts

Browse More Related Video

Physics 15 Torque Example 3 (3 of 7) Mass on Rod and Cable

Physics 15 Torque Example 1 (1 of 7) Mass on Rod and Cable

Physics 15 Torque (19 of 25) More Examples: 1 T=? of Cable Holding Fish

Physics 15 Torque (5 of 27) Tension=? Supporting a Gate

Physics 15 Torque (3 of 27) Tension=? in the Cable

Physics 15 Torque (1 of 27) Boom and Guy Wire

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Torque CalculationStatics ProblemEngineering MechanicsSum of TorquesZero Sum PrincipleGeometrical AnalysisBeam MechanicsForce AnalysisPhysics TutorialProblem SolvingEducational Content