The Definite Integral Part III: Evaluating From The Definition
TLDRThe video script delves into the concept of calculating the area under the curve of the function x squared between the values of 0 and 1. It begins by discussing the approximation of this area using the sum of areas of rectangles, and then refines the process by taking the limit as the number of rectangles approaches infinity. The script introduces the definite integral from 0 to 1 of x squared dx and explains the steps to compute this integral, including determining the width of each subinterval (Δx = 1/n) and selecting the right endpoint for each rectangle (x_i = i * Δx). The video then simplifies the expression and uses a known sum formula for the squares of the first n natural numbers to evaluate the limit as n approaches infinity. The final result is obtained by applying algebraic manipulations to the limit expression, leading to the exact area under the curve x squared from 0 to 1, which is 1/3. This method contrasts with the approximation method, offering an exact value rather than an estimate.
Takeaways
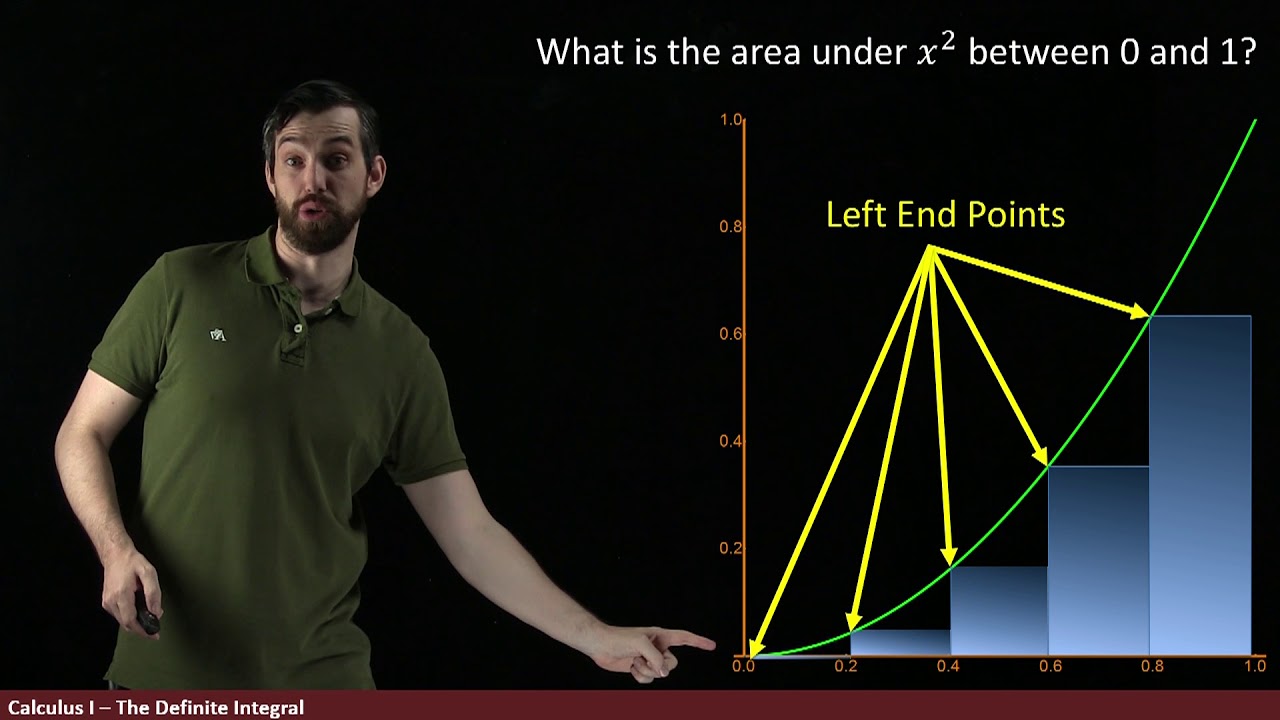
- 📐 The concept discussed is the area under the curve of the function x^2 between 0 and 1.
- 📏 The approximation of the area is achieved by summing the areas of rectangles, which improves as the number of rectangles approaches infinity.
- 🧮 The definite integral from 0 to 1 of x^2 dx is used to find the exact area, symbolized by the limit as n approaches infinity.
- 🔢 The width of each subinterval, Δx, is calculated as 1/n when the interval from 0 to 1 is divided into n parts.
- ➗ The xi values are chosen as the right endpoints of the subintervals, calculated as i * Δx.
- 🔑 The formula for the area is simplified by factoring out constants from the summation, resulting in (1/n^3) * sum from 1 to n of i^2.
- 📈 A mathematical fact is used to express the sum of the squares of the first n natural numbers as n(n + 1)(2n + 1)/6.
- 🎓 The limit as n approaches infinity of the expression (1/n^3) * (n(n + 1)(2n + 1)/6) is computed to find the exact area.
- 📉 The highest power of n in the numerator and denominator is n^3, which allows for the simplification of the limit expression.
- ✅ The final computed area under the curve x^2 from 0 to 1 is exactly 1/3.
- 🔍 The process demonstrates the power of calculus in providing an exact value rather than an approximation.
- 📝 The method involves algebraic manipulation and understanding of limits, showcasing the beauty of calculus in action.
Q & A
What is the main concept being discussed in the transcript?
-The main concept discussed in the transcript is the calculation of the area under the curve of the function x squared between the values of zero and one using the concept of definite integrals and the limit as the number of rectangles (n) approaches infinity.
What is the integral being computed in the transcript?
-The integral being computed is the definite integral from 0 to 1 of the function x squared, denoted as ∫ from 0 to 1 of x^2 dx.
How is the area under the curve approximated using rectangles?
-The area under the curve is approximated by summing the areas of rectangles, where each rectangle's width is Δx (1/n) and height is determined by the function value at a specific point within the rectangle.
What is the chosen method for selecting the height of each rectangle?
-The chosen method for selecting the height of each rectangle is to use the right endpoint of each subinterval, which is calculated as i * Δx, where i is the index of the rectangle.
What is the formula for the width (Δx) of each subinterval when the interval is divided into n parts?
-The formula for the width (Δx) of each subinterval is 1/n, which represents the original width of 1 divided into n equal parts.
What is the expression used to represent the sum of the squares of the first n natural numbers?
-The expression used to represent the sum of the squares of the first n natural numbers is n(n + 1)(2n + 1) / 6.
How is the final limit computed in the transcript?
-The final limit is computed by substituting the sum of the squares of the first n natural numbers into the integral expression, simplifying the expression, and then evaluating the limit as n approaches infinity.
What is the result of the computed limit that represents the area under the curve?
-The result of the computed limit is 1/3, which is the exact area under the curve of x squared between the points 0 and 1.
Why is the method of taking the limit as n approaches infinity considered superior to using a finite number of rectangles?
-The method of taking the limit as n approaches infinity is considered superior because it provides an exact value for the area under the curve, whereas using a finite number of rectangles only provides an approximation.
What is the significance of the definite integral in calculus?
-The definite integral in calculus is significant because it allows for the calculation of the exact area under a curve between two points, which has wide applications in various fields including physics, engineering, and economics.
How does the process of using limits in calculus help in finding the area under a curve?
-The process of using limits in calculus helps in finding the area under a curve by allowing for an infinite number of infinitesimally small rectangles to be summed, which converges to the exact area as the number of rectangles increases without bound.
What mathematical technique can be used to prove the formula for the sum of the squares of the first n natural numbers?
-The formula for the sum of the squares of the first n natural numbers can be proven using mathematical induction, which is a method of mathematical proof typically used for establishing the truth of a proposition for all natural numbers.
Outlines
📊 Understanding the Definite Integral of x^2 from 0 to 1
This paragraph introduces the concept of finding the area under the curve of the function x^2 between 0 and 1. It discusses the approximation of this area using rectangles and the process of taking the limit as the number of rectangles (n) approaches infinity to achieve a more accurate approximation. The paragraph also explains the calculation of the definite integral, using the formula for the limit as n approaches infinity of the sum of x_i^2 * Δx, where Δx is 1/n and x_i is chosen as the right endpoint of each subinterval. The process involves determining the width of each subinterval (Δx) and the specific x values (x_i) to compute the area.
🔍 Evaluating the Definite Integral to Find the Exact Area
The second paragraph delves into the computation of the definite integral to find the exact area under the curve x^2 from 0 to 1. It explains the process of simplifying the formula by factoring out constants and using a known sum formula for the series of squares (1^2 + 2^2 + ... + n^2 = n(n + 1)(2n + 1)/6). The paragraph concludes by calculating the limit as n approaches infinity, which results in the area being equal to 1/3. This method contrasts with the rectangle approximation, which provides an estimate but not the exact value. The paragraph emphasizes the power of calculus in providing an exact numerical answer to the problem.
Mindmap
Keywords
💡Area under a curve
💡Rectangle approximation
💡Limit
💡Definite integral
💡Subintervals
💡Right endpoint
💡Summation
💡Index variable
💡Polynomial
💡Mathematical induction
💡Exact value
Highlights
The concept of finding the area under the curve of the function x squared between the values of zero and one is introduced.
Approximation of the area using the sum of areas of rectangles is discussed.
The idea of taking the limit as the number of rectangles approaches infinity to improve the approximation is explained.
The process of using definite integral calculus to find an exact value for the area is described.
The integral is expressed as a limit of a sum involving xi squared and delta x.
The width of each subinterval (delta x) is determined to be 1/n.
The choice to use the right endpoint for xi is made to simplify the calculation.
A formula for xi in terms of i and delta x is derived and tested for validity.
The formula for the area under the curve is simplified by factoring out constants from the summation.
A known mathematical fact about the sum of squares from 1 to n is used to further simplify the integral.
The sum from 1 to n of i squared is shown to be equal to n(n + 1)(2n + 1)/6.
The limit as n approaches infinity is taken to find the exact value of the integral.
The highest power of n in the polynomial expression is identified to evaluate the limit.
The final value of the area under x squared from 0 to 1 is determined to be 1/3.
The difference between the approximation using finite rectangles and the exact value obtained through calculus is highlighted.
The importance of the definite integral in providing an exact value rather than an approximation is emphasized.
The process of evaluating the integral using algebraic manipulation and limits is outlined.
The video concludes with the understanding that the area under x squared from 0 to 1 is exactly 1/3, a significant result in calculus.
Transcripts
Browse More Related Video

Riemann sums in summation notation | Accumulation and Riemann sums | AP Calculus AB | Khan Academy

The Definite Integral Part II: Using Summation Notation to Define the Definite Integral
The Definite Integral Part I: Approximating Areas with rectangles

Finding The Area Using The Limit Definition & Sigma Notation

Math 1325 Lecture 13 2

BusCalc 13.4 Riemann Sums
5.0 / 5 (0 votes)
Thanks for rating: