Math 1325 Lecture 13 2

Michael Bailey

17 May 201614:37

EducationalLearning

32 Likes 10 Comments

TLDRThis lecture delves into the concept of definite integrals, which are used to calculate the area under a curve between two points on the x-axis. The process begins with an approximation using rectangles, which becomes more precise as the number of rectangles increases. The lecture explains how to use the right or left edge values of the rectangles to estimate the area, and how this leads to the fundamental theorem of calculus, which connects derivatives and integrals. The definite integral is defined as the limit of the sum of rectangle areas as the number of rectangles approaches infinity. The lecturer demonstrates how to calculate definite integrals with specific examples, including the integral of x squared from 0 to 1, and highlights the properties of definite integrals, such as the integral from a point to itself being zero and the integral over a reversed interval being the negative of the original. The lecture concludes with a more complex integral problem, showcasing the use of substitution to simplify the integral and the application of integral properties. The summary emphasizes the practicality and importance of definite integrals in calculus and their role in determining areas under curves.

Takeaways

📐 The concept of a definite integral is used to calculate the area under a curve from one point to another, which can provide valuable information about the behavior of a function.
📈 The area under a curve can be estimated using rectangles, with the height determined by the function's value at the right or left edge of each interval.
🔍 As the number of rectangles increases, the approximation of the area under the curve becomes more accurate, approaching the actual area.
🧮 The width of each rectangle in the approximation is the interval length divided by the number of rectangles.
∫ The definite integral is represented by an integral sign with limits, and it is evaluated by substituting the upper limit into the antiderivative and subtracting the value obtained by substituting the lower limit.
📉 The definite integral of a function from a to b can be found using the antiderivative of the function, applying the fundamental theorem of calculus.
🔁 If the limits of integration are the same, the value of the definite integral is zero, as there is no area to calculate.
↔️ The value of a definite integral is the negative of the integral evaluated in the reverse order of limits, meaning the integral from B to A is the negative of the integral from A to B.
📚 The process of finding a definite integral involves first finding the antiderivative of the function, then evaluating it at the given limits.
📉 The definite integral is a powerful tool in calculus that can be used to find areas, volumes, central points of mass, and other quantities of interest in various fields.
📝 Practice is key to understanding and applying the concept of definite integrals, as it involves both conceptual understanding and the ability to perform calculations accurately.

Q & A

What is the primary purpose of calculating the area under a function curve in calculus?
-The primary purpose of calculating the area under a function curve is to provide interesting information about the function, which can be used in various applications such as business and social sciences.
How is the area under a curve represented in calculus?
-The area under a curve is represented by the definite integral from the domain from x equals a to x equals b, and is often depicted as a blue shaded area in a graph.
What is the basic approach to estimate the area under a curve when dealing with a function like y = x^2?
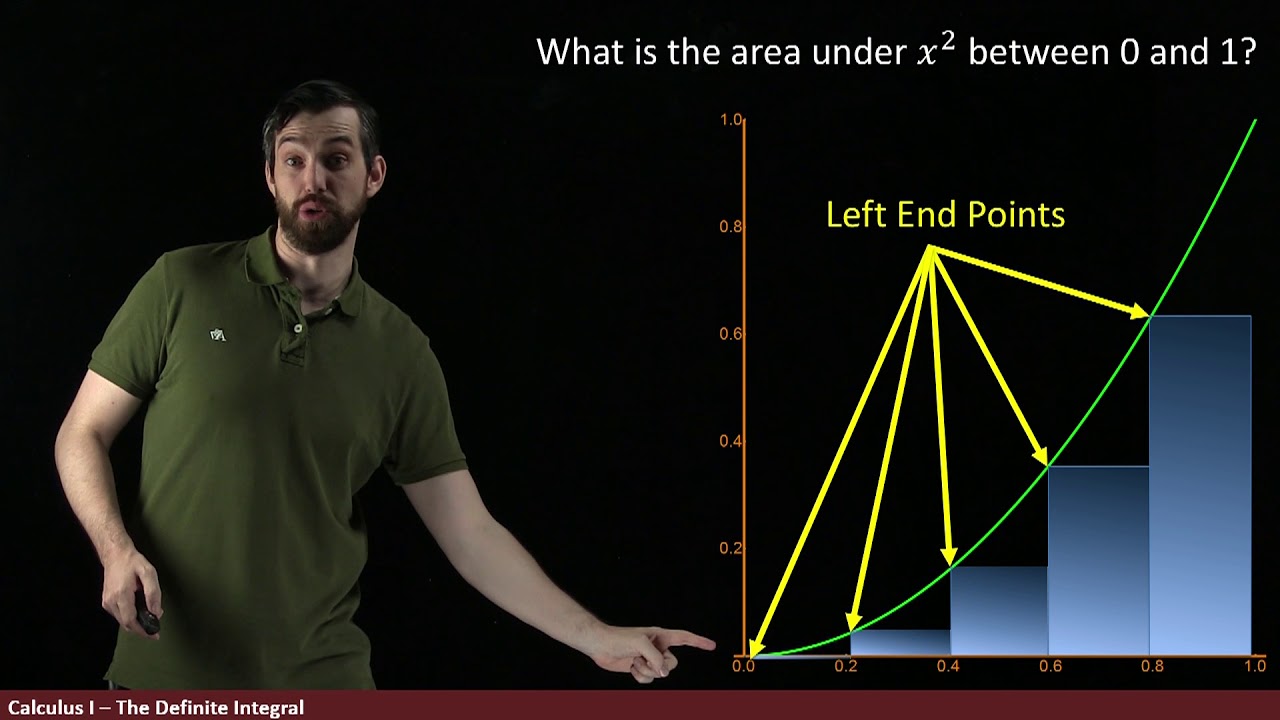
-The basic approach is to divide the interval into sections and use rectangles with heights determined by the function at the right edge of each interval to estimate the area under the curve.
Why is the initial estimate of the area under the curve considered an overestimate when using rectangles with right edge values?
-The initial estimate is considered an overestimate because the rectangles extend above the curve, rather than hugging the curve's shape, leading to a larger calculated area.
How does the accuracy of the area estimation improve as the number of rectangles increases?
-As the number of rectangles increases, the width of each rectangle decreases, leading to a more precise approximation of the curve's shape and thus a more accurate estimate of the area.
What is the general formula for the area under a curve using the limit concept?
-The general formula is the limit as n approaches infinity of the sum of the areas of the rectangles, which can be represented as ∫(f(x) * Δx) from a to b, where Δx is the interval length divided by the number of rectangles.
What is the significance of the definite integral in calculus?
-The definite integral is significant because it provides a method to calculate the exact area under a curve over a defined interval, which is a fundamental concept in calculus.
How does the process of evaluating a definite integral differ from an indefinite integral?
-A definite integral involves specific limits and provides a numerical answer, representing the exact area under the curve between those limits. An indefinite integral, on the other hand, does not have limits and results in a function plus a constant (C), representing the antiderivative of the integrand.
What is the Fundamental Theorem of Calculus, and how does it relate to definite integrals?
-The Fundamental Theorem of Calculus states that the definite integral of a function can be found by evaluating the antiderivative of the function at the upper limit and subtracting the evaluation at the lower limit. It is fundamental because it connects differentiation and integration, providing a method to calculate definite integrals.
What happens when you evaluate an integral from a point to the same point?
-When you evaluate an integral from a point to the same point, the result is 0. This makes sense because there is no area under a curve that has no 'mass' or spans no distance.
How can you simplify the process of evaluating a definite integral with a substitution?
-You can simplify the process by converting the limits of integration to match the substitution variable (u). This allows you to directly plug the new limits into the simplified integral without having to revert back to the original variable (x).

Outlines

00:00

📐 Understanding Definite Integrals and Area Under Curves

This paragraph introduces the concept of definite integrals in the context of calculus for business and social sciences. It explains how the area under a function curve, such as y = f(x), can be calculated using rectangles to approximate the area. The process involves dividing the interval [a, b] into sections and using the function's value at the right or left edge of each section to determine the height of the rectangles. As the number of rectangles increases, the approximation becomes more accurate, converging to the actual area under the curve. The paragraph also touches on the concept of derivatives and how it relates to the calculation of the area.

05:01

🧮 Calculating Definite Integrals and the Fundamental Theorem of Calculus

The second paragraph delves into the calculation of definite integrals, emphasizing the difference between definite and indefinite integrals. It outlines the process of finding the area under a curve by evaluating the integral of a function, such as x squared, from a lower limit to an upper limit. The paragraph explains the steps to find the indefinite integral, followed by evaluating it between specific limits to get the definite integral. The Fundamental Theorem of Calculus is introduced, which connects the process of integration with the calculation of areas. Several examples are provided to illustrate the computation of definite integrals, highlighting the importance of practice in mastering the technique.

10:02

∫ Properties of Definite Integrals and Advanced Integration Techniques

The final paragraph discusses properties of definite integrals, such as the result of integrating a function from a point to itself being zero, and the reversal of limits resulting in the opposite value of the integral. It also covers advanced integration techniques, including substitution, which simplifies the process of integrating complex functions. The paragraph provides an example of integrating a function of x cubed minus 3x squared, demonstrating how substitution can make the limits of integration easier to work with. The lecture concludes with a reminder of the importance of practice and the significance of definite integrals in calculus.

Mindmap

Keywords

💡Definite Integral

A definite integral is a fundamental concept in calculus that represents the area under a curve between two points on the x-axis. It is defined as the limit of the sum of rectangle areas as the number of rectangles approaches infinity. In the video, the definite integral is used to calculate the area under the curve of a function, such as y = x^2, from 0 to 1, which is a key part of the lecture's theme.

💡Rectangle Estimation

Rectangle estimation is a method used to approximate the area under a curve by dividing the area into rectangles and summing their areas. In the context of the video, this technique is employed to estimate the area under the curve y = x^2 from 0 to 1 by dividing the interval into four sections and using the right edge value to determine the height of each rectangle.

💡Function Curve

A function curve, also known as a graph, is a visual representation of a mathematical function where one variable is represented on the y-axis and the other on the x-axis. In the video, the function curve y = f(x) is used to illustrate the concept of calculating the area under the curve, which is the main focus of the lecture.

💡Derivative

The derivative is a concept in calculus that represents the rate of change of a function at a certain point. It is related to the slope of the tangent line to the graph of the function at a given point. While the video focuses on integrals, the concept of derivatives is mentioned in the context of how the derivative is derived from the slopes of secants using limits, which is a precursor to understanding integrals.

💡Integral

An integral is a mathematical concept that represents the area under a curve, which can be thought of as the reverse process of differentiation. In the video, integrals are used to calculate areas under curves and are central to the discussion of how to estimate and find the area under a function curve using limits and rectangles.

💡Limits

In calculus, limits are a way to describe the behavior of a function as the input approaches a certain value. The video discusses how limits are used in the context of integrals to find the area under a curve by taking the limit as the number of rectangles approaches infinity.

💡Indefinite Integral

An indefinite integral represents an antiderivative of a function, which is a function whose derivative is the original function. Unlike a definite integral, it does not have specific limits and is often denoted by an '∫' symbol without numerical bounds. In the video, the indefinite integral is mentioned in contrast to the definite integral, highlighting the difference in their applications and interpretations.

💡Fundamental Theorem of Calculus

The Fundamental Theorem of Calculus is a theorem that links the concept of differentiation and integration, stating that the definite integral of a function can be found by finding the antiderivative of the function and subtracting the value of the antiderivative at the lower limit from the value at the upper limit. In the video, this theorem is emphasized as a central principle in calculus that allows for the calculation of definite integrals.

💡Substitution

Substitution is a technique used in calculus to simplify the process of integration by changing variables to make the integral easier to compute. In the video, substitution is briefly mentioned as a method to deal with more complex integrals, such as when integrating functions of the form x^n where n is a rational number.

💡Power Rule

The power rule is a basic rule in calculus that allows for the integration of polynomial functions. It states that the integral of x^n, where n is a constant, is (x^(n+1))/(n+1) + C, where C is the constant of integration. The video references the power rule when discussing the integration of x^2 and other polynomial functions.

💡Integration by Parts

Integration by parts is a method of integration used for the integral of two functions multiplied together, often denoted as ∫u dv. Although not explicitly detailed in the video, it is an advanced technique that might be implied when discussing more complex integrals, and it is closely related to the product rule for differentiation.

Highlights

Calculating the area under function curves provides interesting information about the function.

The area under a curve is represented by the blue shaded area from domain x=a to x=B.

Using rectangles to estimate the area under a parabola y=x^2 from 0 to 1.

The height of each rectangle is determined by plugging the x-value into the function y=x^2.

The area under the curve is approximately equal to 1/2 using the right edge values of the rectangles.

Using the left edge values results in an underestimate of the area.

As the number of rectangles increases, the estimate gets closer to the actual area.

The area under a curve equals the sum of the areas of the rectangles as the number of rectangles approaches infinity.

The width of each rectangle equals the interval length divided by the number of rectangles.

The general formula for the area under a curve is the limit as n approaches infinity of the sum of f(x) times Delta X.

The definite integral of x^2 from 0 to 1 gives the actual area under the curve.

The definite integral is evaluated at specific values and is represented by an integral sign with numbers on it.

The Fundamental Theorem of Calculus relates the definite integral to the antiderivative of the function.

Evaluating an integral from the same point (A to A) results in a value of 0, indicating no area under a single point.

The value of the integral from B to A is the opposite of the value from A to B, reflecting the change in limits.

Integration by substitution can simplify complex integrals by changing variables to match the form of the integrand.

When evaluating an integral over the same limits with a substitution, the result is 0 due to the property of integrals.

Definite integrals are straightforward to calculate once the antiderivative is found and limits are applied.

Transcripts

Browse More Related Video

Business Calculus - Math 1329 - Section 5.3 - The Definite Integral and Fundamental Thm of Calculus

What Is an Integral?

Riemann Sums and Definite Integrals

AP Calculus AB: Lesson 6.2 Part 2 (Limit Definition of Definite Integral)

The Definite Integral Part III: Evaluating From The Definition

The Definite Integral Part I: Approximating Areas with rectangles

Math 1325 Lecture 13 2

Takeaways

Q & A

What is the primary purpose of calculating the area under a function curve in calculus?

How is the area under a curve represented in calculus?

What is the basic approach to estimate the area under a curve when dealing with a function like y = x^2?

Why is the initial estimate of the area under the curve considered an overestimate when using rectangles with right edge values?

How does the accuracy of the area estimation improve as the number of rectangles increases?

What is the general formula for the area under a curve using the limit concept?

What is the significance of the definite integral in calculus?

How does the process of evaluating a definite integral differ from an indefinite integral?

What is the Fundamental Theorem of Calculus, and how does it relate to definite integrals?

What happens when you evaluate an integral from a point to the same point?

How can you simplify the process of evaluating a definite integral with a substitution?