Finding The Area Using The Limit Definition & Sigma Notation

The Organic Chemistry Tutor
9 Mar 201813:18
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explains the process of finding the area under a curve using the limit definition. It illustrates the concept with the function f(x) = x^3 over the closed interval from 0 to 8. The explanation includes calculating the area as the limit of the sum of rectangles' areas as the number of rectangles approaches infinity. The script also details the use of right endpoints and the summation formula for i^3, leading to the correct area calculation. The process is further validated by comparing it with the result of the definite integral.

Takeaways
  • πŸ“Š The video focuses on finding the area under a curve using the limit definition.
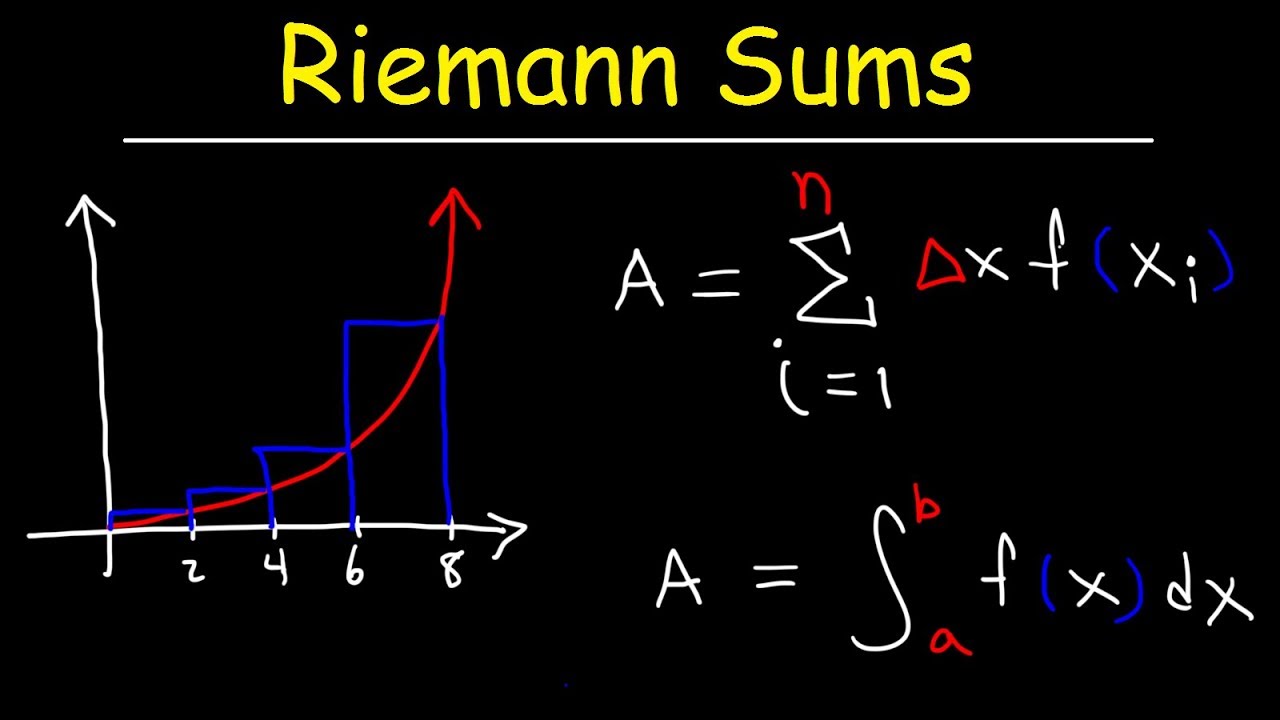
  • 🧩 The area of the shaded region between the x-axis and a curve over a closed interval can be found using the limit of the sum of rectangles' areas.
  • πŸ“ˆ The formula for calculating the area is the limit as n approaches infinity of the sum of f(x_i) * Ξ”x, where f(x_i) is the height and Ξ”x is the width of the rectangles.
  • πŸ”’ For right endpoints, x_i is calculated as a + Ξ”x * i, where 'a' is the start of the interval and 'b' is the end.
  • 🎨 The illustration in the video uses the function f(x) = x^3 on the interval [0, 8] with n=4 for demonstration purposes.
  • πŸ“ The width of each subinterval, Ξ”x, is calculated as (b - a) / n.
  • πŸ› οΈ The actual problem involves letting n approach infinity, leaving Ξ”x as 8/n.
  • πŸ“Š The summation formula for i^3 from i=1 to n is (n^2 * (n + 1)^2) / 4.
  • πŸ” The limit and summation are applied to find the area, which simplifies to 1024.
  • πŸ”§ The video also suggests confirming the result by calculating the definite integral of the function from a to b, which yields the same result.
  • πŸŽ“ For more information on summation formulas, the video recommends referring to a related video on the topic.
Q & A

  • What is the main focus of the video?

    -The main focus of the video is to explain how to find the area under a curve using the limit definition, specifically for the function f(x) = x^3 over the closed interval from 0 to 8.

  • What is the formula for calculating the area under a curve using the limit definition?

    -The formula for calculating the area under a curve using the limit definition is the limit as n approaches infinity of the sum of the rectangles' areas, which is given by βˆ‘(f(x_i) * Ξ”x) from i=1 to n, where f(x_i) is the height of the rectangle and Ξ”x is its width.

  • How is the width of each subinterval (Ξ”x) calculated?

    -The width of each subinterval (Ξ”x) is calculated as (b - a) / n, where 'a' is the start of the interval, 'b' is the end, and 'n' is the number of rectangles.

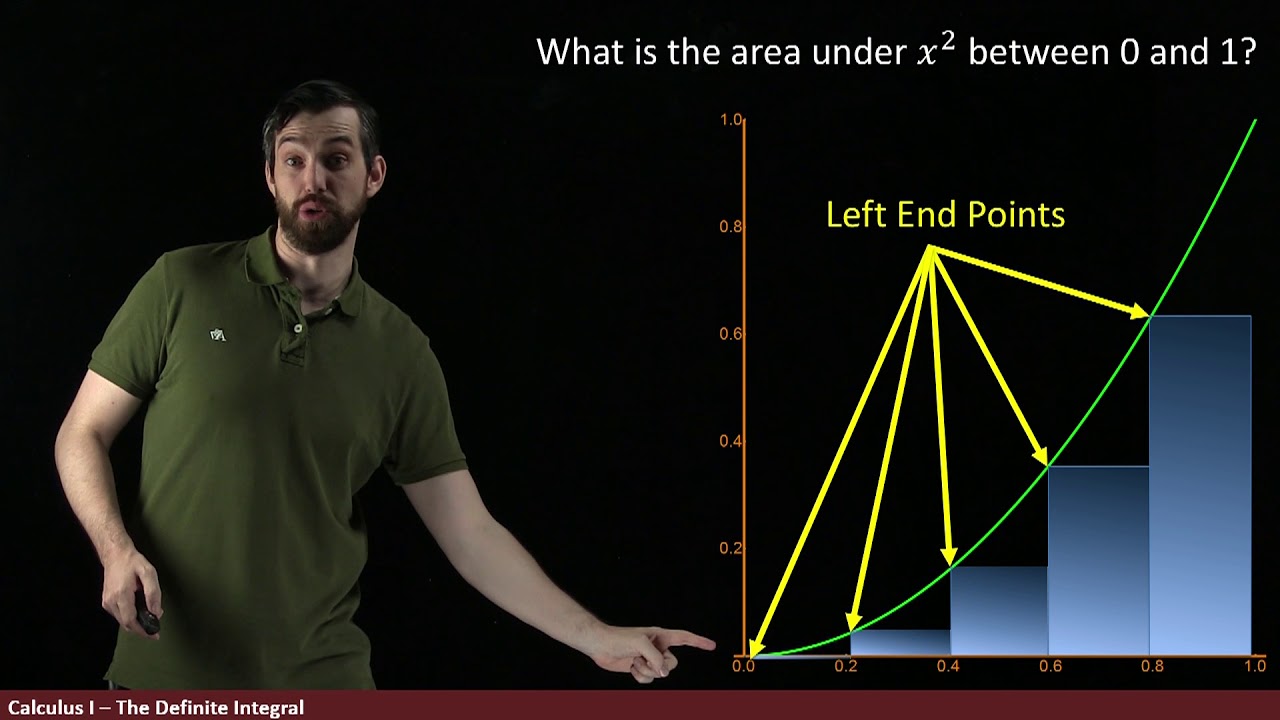
  • What are the two different types of endpoints that can be used in the calculation?

    -The two different types of endpoints that can be used in the calculation are the right endpoints and the left endpoints.

  • How is the x-coordinate for a right endpoint calculated?

    -The x-coordinate for a right endpoint is calculated as 'a' plus 'Ξ”x' times 'i', where 'a' is the start of the interval and 'i' is the subscript of the point.

  • What is the significance of the summation formula in this context?

    -The summation formula is used to find the sum of the areas of the rectangles, which is necessary for applying the limit definition to find the area under the curve.

  • How is the summation formula for i^3 from i=1 to n expressed?

    -The summation formula for i^3 from i=1 to n is given by (n^2 * (n + 1)^2) / 4.

  • What is the anti-derivative of f(x) = x^3?

    -The anti-derivative of f(x) = x^3 is F(x) = x^4/4 + C, where C is the constant of integration.

  • How does the definite integral confirm the area calculated using the limit definition?

    -The definite integral confirms the area by evaluating the antiderivative of the function over the interval, which should yield the same result as the limit definition if calculated correctly.

  • What is the final calculated area under the curve using the limit definition?

    -The final calculated area under the curve using the limit definition is 1024 square units.

  • What is the result of evaluating the definite integral of f(x) = x^3 from 0 to 8?

    -The result of evaluating the definite integral of f(x) = x^3 from 0 to 8 is 4096/4 - 0 = 1024.

Outlines
00:00
πŸ“Š Introduction to Finding Area Using Limit Definition

This paragraph introduces the concept of finding the area of a shaded region between the x-axis and a curve over a closed interval using the limit definition. It sets the stage for the problem by presenting a function, x cube, and the interval from 0 to 8. The paragraph explains that the area can be approximated using an infinite number of rectangles, with the height represented by the function value at each point and the width by delta x. The key formula for calculating the area is introduced, which involves the sum of rectangles' areas as n approaches infinity. The paragraph also explains how to find x sub i for right endpoints and illustrates this with a number line example where n is 4, calculating delta x and the x values for each subinterval.

05:01
πŸ“ Calculating x sub i and Delta x for Right Endpoints

This paragraph delves into the specifics of calculating x sub i and delta x for right endpoints in the process of finding the area under a curve. It continues from the previous example, explaining how to determine x sub i along the number line and how to calculate delta x when the interval extends to infinity. The paragraph walks through the process of evaluating the function at each x sub i value over the interval from 0 to 8 and emphasizes the importance of using the summation formula for i cubed. It also provides a detailed explanation of how to apply the limit as n approaches infinity to the summation, leading to the calculation of the area.

10:01
πŸ”’ Confirmation of Area Through Definite Integral

The final paragraph focuses on confirming the calculated area using the definite integral of the function. It explains that the area under the curve is equal to the definite integral of the function from a to b. The paragraph provides a step-by-step calculation of the definite integral by finding the antiderivative of x cubed and evaluating it between the interval's endpoints. The result obtained from the definite integral is compared with the area calculated using the limit definition, confirming the accuracy of the previous calculation. The paragraph emphasizes the efficiency of using definite integrals for such problems but also highlights the importance of understanding the limit definition as a foundational concept.

Mindmap
Keywords
πŸ’‘Limit definition
The limit definition is a fundamental concept in calculus used to define the area under a curve. In the context of the video, it is used to calculate the area of the shaded region between the x-axis and the curve of the function x cube over the closed interval from 0 to 8. The limit definition involves taking the limit as the number of rectangles (n) approaches infinity, summing up the areas of these rectangles to approximate the area under the curve.
πŸ’‘Rectangles
Rectangles are geometric figures used in the process of finding the area under a curve through the limit definition. In the video, rectangles are imagined to cover the shaded region between the curve and the x-axis. The area of each rectangle is calculated by multiplying the function's value at a particular point (height) by the width of the interval (delta x). As the number of rectangles increases (n approaches infinity), the total area approximated by these rectangles converges to the actual area under the curve.
πŸ’‘Delta x
Delta x represents the width of the subintervals created along the x-axis when using the limit definition to find the area under a curve. It is calculated as the total length of the interval (b - a) divided by the number of rectangles (n). In the limit definition, as n approaches infinity, delta x approaches zero, leading to an infinite number of infinitesimally small rectangles that closely approximate the area under the curve.
πŸ’‘Right endpoints
Right endpoints refer to the points on the number line that correspond to the farthest edge of each subinterval when using the limit definition to approximate areas under a curve. In the video, the right endpoints are used to determine the x-values for the top of each rectangle, which are then used to find the function values (heights) and calculate the area of each rectangle.
πŸ’‘Summation formula
The summation formula is a mathematical expression used to find the sum of a series of terms. In the context of the video, it is used to sum the areas of the rectangles (i to the third power) from i=1 to i=n, which is necessary for applying the limit definition to find the area under the curve. The summation formula for i cubed is key in simplifying the expression for the area.
πŸ’‘Definite integral
The definite integral is a fundamental concept in calculus that represents the signed area under a curve between two points on the x-axis. It is used to confirm the result obtained from the limit definition in the video. The definite integral of a function from a to b is denoted as the integral from a to b of f(x) dx, and it provides a precise value for the area under the curve.
πŸ’‘Anti-derivative
The anti-derivative, also known as the indefinite integral, is a function that represents the reverse process of differentiation. It is used to find the original function from its derivative, which is essential when calculating definite integrals. In the video, the anti-derivative of x cubed is x to the fourth over four, which is used to evaluate the definite integral and confirm the area under the curve.
πŸ’‘Closed interval
A closed interval is a set of real numbers that includes its endpoints. In the video, the closed interval from 0 to 8 represents the range on the x-axis over which the area under the curve of the function x cube is to be calculated. The closed interval is important as it defines the limits within which the area is being determined.
πŸ’‘Function values
Function values are the results obtained by substituting a value into a function. In the video, function values are used to determine the height of each rectangle in the approximation of the area under the curve. The function value at a specific x-value (f(x_i)) is crucial for calculating the area of each rectangle using the limit definition.
πŸ’‘Sigma notation
Sigma notation, also known as summation notation, is a mathematical shorthand used to represent the sum of a sequence of terms. In the video, sigma notation is used to express the sum of the function values (f(x_i)) times delta x over the interval from 0 to 8 as n approaches infinity. This notation simplifies the expression of the limit definition for the area under a curve.
πŸ’‘Area calculation
Area calculation is the process of determining the size of a two-dimensional region. In the video, area calculation is the main focus, where the limit definition of integrals is used to find the area under the curve of the function x cube over a closed interval. The area is calculated by summing the areas of rectangles that approximate the region and taking the limit as the number of rectangles approaches infinity.
Highlights

The video focuses on finding the area using the limit definition.

The function of interest is x cubed, and the interval is from 0 to 8.

The area of the shaded region is approximated by summing the areas of rectangles.

The limit definition involves an infinite number of rectangles to approximate the area under the curve.

The width of each rectangle is represented by delta x.

The height of the rectangle is given by the function value at each point, f(x_sub_i).

For the illustration, n is set to 4, and the interval is divided into 4 subintervals.

Delta x is calculated as (b - a) / n, which in this case is 8 / 4 = 2.

The right endpoints are used for simplicity in the illustration.

The x values for the right endpoints are 2, 4, 6, and 8.

The area calculation involves the limit as n approaches infinity.

The summation notation (sigma) is introduced for the sum of the areas of the rectangles.

The summation formula for i cubed is applied to find the area.

The final area calculation is 1024, using the summation and limit definition.

The area is confirmed by calculating the definite integral of the function from 0 to 8.

The anti-derivative of x cubed is x to the fourth over 4.

The definite integral confirms the area is 1024, matching the previous calculation.

Transcripts

Browse More Related Video

The Definite Integral Part III: Evaluating From The Definition

The Definite Integral Part I: Approximating Areas with rectangles

Riemann Sums - Left Endpoints and Right Endpoints

BusCalc 13.4 Riemann Sums

Math 1325 Lecture 13 2

The Definite Integral Part II: Using Summation Notation to Define the Definite Integral

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Integral CalculusLimit DefinitionArea CalculationMathematics Tutorialx^3 FunctionSummation FormulasInfinite SeriesEducational ContentCalculus ConceptsMath Video