Math1325 10 4 Lecture - Applications for Maximum & Minimum
TLDRThis lecture explores the application of derivatives to find maxima and minima in business and social science problems. The first problem involves a company's employee growth, modeled by the formula n(T) = (8 * (1 + (160/T))) / (T^2 + 16), where T is the number of years after 2015. By taking the derivative and applying it to the limited domain of T (years after 2015), the maximum number of employees is found to be 168 in the year 2019. The second problem focuses on minimizing the cost of fencing a rectangular pasture with a given area, where one side is along a road with a higher fence cost. The solution involves setting up a cost function based on the cost per foot of fencing and the dimensions of the rectangle, leading to the dimensions that minimize the cost. The third problem deals with minimizing the total cost of production and storage for a certain number of items over a year. By formulating the cost function and taking its derivative, the optimal number of items per production run is determined to minimize costs. The lecture emphasizes the importance of understanding the context and the question, as well as the process of setting up and solving equations related to the problem at hand.
Takeaways
- 📈 Maximizing and minimizing problems often involve applying derivatives to find optimum values in business and social science contexts.
- 🔍 Start with the end in mind: Always read the last sentence of a word problem first to understand what you are solving for, which helps in contextualizing the problem.
- 🧮 When dealing with limited domains, compare the derivative at zero, as well as at the endpoints of the domain.
- 📌 For maxima and minima problems, interpret the results in the context of the problem to ensure the solution makes sense.
- 📐 In optimization problems, express the quantity to be maximized or minimized as a function of one variable, using constraints to eliminate other variables.
- 🤔 Break down complex word problems into smaller, manageable parts to avoid becoming overwhelmed.
- 💰 In cost minimization problems, consider both fixed costs (like fencing along a road) and variable costs (like fencing the remaining sides of a field).
- 📐 Use the area of a rectangle (length times width) as a constraint to express one variable in terms of another when optimizing dimensions.
- 🔢 When setting up cost functions, ensure all costs are included, such as production runs, items per run, and storage costs.
- 📉 Take the derivative of the cost function with respect to the variable of interest and set it to zero to find the critical points for optimization.
- 🔄 Perform a second derivative test to confirm that the critical points found do indeed correspond to a minimum or maximum.
- ⚖️ When solving for dimensions that minimize costs, ensure to consider both the cost per unit of length and the total perimeter or area involved.
Q & A
What is the formula given to predict the growth of a company over the next 10 years?
-The formula given to predict the growth of the company is n(T) = (8 * (1 + (160/T))) / (T^2 + 16), where n is the number of employees and T is the number of years after 2015.
How does one determine the year when the number of employees will be maximized?
-To determine the year when the number of employees will be maximized, you take the derivative of the given formula with respect to T, set it equal to zero, and solve for T. Also, check the endpoints of the domain, in this case, T=0 and T=10 years.
What is the significance of starting with the last sentence of a word problem?
-Starting with the last sentence helps to ground you in the context of the problem and allows you to focus on what is being asked. It helps in identifying the key elements of the problem and the variables involved.
What is the maximum number of employees the company will have according to the problem?
-The maximum number of employees the company will have is 168, which occurs in the year 2019 (T=4 years after 2015).
How do you approach a problem where you need to minimize the cost of a rectangular field?
-First, identify the constraints and the variables involved. Then, express the cost as a function of one variable by using the given constraints, such as the area of the rectangle. After that, take the derivative of the cost function and set it to zero to find the minimum cost.
What is the cost function for the rectangular field problem, given the cost of fencing along the road and the remaining sides?
-The cost function for the rectangular field is 25X + 10Y, where X is the length along the road and Y is the length perpendicular to the road.
What is the area of the rectangular pasture that the farmer needs to enclose?
-The area of the rectangular pasture that the farmer needs to enclose is 1,600,000 square feet.
What is the cost per foot for fencing along the road and the remaining sides?
-The cost per foot is $15 for fencing along the road and $10 for the remaining sides.
What are the dimensions of the pasture that minimize the cost?
-The dimensions of the pasture that minimize the cost are 800 feet by 200 feet.
What is the total cost function for the production and storage of items, considering the cost per production run and cost per item?
-The total cost function is (1,000,000 / X * 800) + (1,000,000 * 6) + (X/2 * 1), where X is the number of items in each production run.
How many items should be in each production run to minimize the total cost?
-To minimize the total cost, there should be 40,000 items in each production run.
What is the role of the second derivative test in this context?
-The second derivative test is used to confirm that the value found for X (40,000 items) indeed corresponds to a minimum point for the cost function, ensuring that the cost is minimized at this production run size.
Outlines
📈 Finding Maximum Employee Growth Over Time
The first paragraph discusses the application of derivatives to find the maximum number of employees a company will have over a period of time. The formula provided is n(T) = (8 * (1 + 160/T)) / (T^2 + 16), where n is the number of employees and T is the number of years after 2015. The focus is on determining the year when the number of employees will be at its maximum. The lecturer emphasizes starting with the question to understand the context and then applying the derivative to the formula. The domain is limited to T = 0 to T = 10 years. The derivative n'(T) is calculated, and the critical points are found by setting the numerator to zero, yielding T = ±4. Since time cannot be negative, only T = 4 is considered. The maximum number of employees is found by substituting T = 4 back into the original equation, resulting in 168 employees in the year 2019. The starting point (T = 0) corresponds to the initial 8 employees, and T = 10 yields 118 employees.
🏗️ Minimizing Fence Cost for a Rectangular Field
The second paragraph explores a problem where a farmer needs to minimize the cost of fencing a rectangular pasture with a given area of 1,600,000 square feet. One side of the rectangle borders a road, requiring a more expensive fence costing $15 per foot, while the other two sides will cost $10 per foot. The side perpendicular to the road is bounded by a river, eliminating the need for a fence. The cost function is derived as 25X + 10Y, where X is the length of the road-side fence and Y is the length of the other two sides. Using the area constraint XY = 1,600,000, the cost function is expressed in terms of a single variable, X. The derivative of the cost function is taken, and the minimum cost is found by setting the derivative to zero. The solution X = 800 feet is obtained, which corresponds to a width of 2,000 feet for the pasture, thus minimizing the cost.
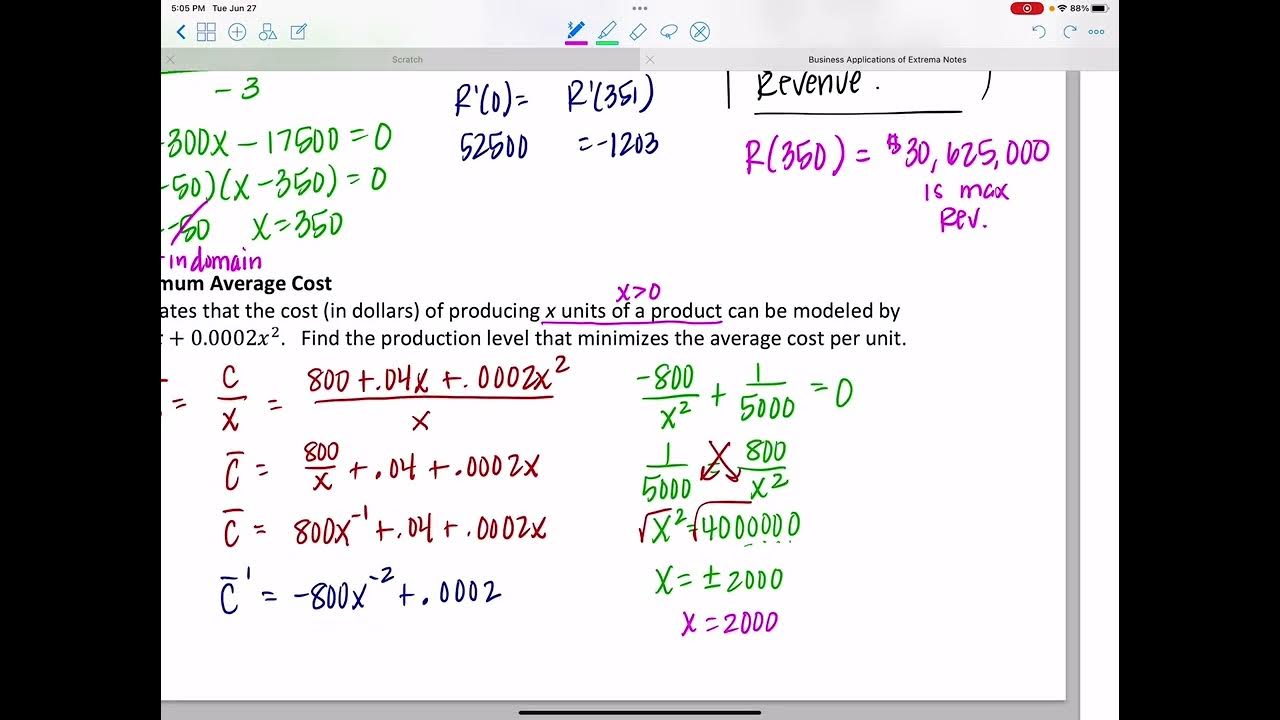
🔄 Minimizing Total Production and Storage Costs
The third paragraph addresses a scenario where a company needs to minimize the total cost of production and storage for a million items over a year. The production costs include a fixed cost of $800 per production run and a variable cost of $6 per item. Storage costs are $1 per item for a year, with half of each production run being stored. The total cost function is derived by adding the production costs (number of runs times $800 plus the number of items times $6) and the storage costs (half the number of items times $1). The total cost function is then simplified to include only the variable X, which represents the number of items per production run. The derivative of the total cost function is taken, and the minimum cost condition is found by setting the derivative to zero. The solution X = 40,000 items per run is obtained, which minimizes the total cost of production and storage.
📊 Analyzing Production Run Size for Cost Efficiency
The fourth paragraph continues the discussion on minimizing costs, focusing on the optimal size of each production run. The total cost function is given as one million divided by X times 800 plus six million. The storage costs are considered as half of each production run's items stored at a cost of $1 per item. The total cost function combines both production and storage costs. By taking the derivative of the total cost with respect to X and setting it to zero, the optimal number of items per production run is determined to be 40,000. This number minimizes the total cost of production and storage. A second derivative test is mentioned to confirm that the result indeed represents a minimum.
Mindmap
Keywords
💡Derivatives
💡Maxima and Minima
💡Word Problems
💡Optimization
💡Quotient Rule
💡Limited Domain
💡Constraints
💡Cost Function
💡Second Derivative Test
💡Area of a Rectangle
💡Production Run
Highlights
The lecture focuses on applying derivatives to find optimum values in business and social science problems.
A formula is provided to predict the growth of a company over time, which is used to determine the maximum number of employees.
The importance of starting with the question when approaching word problems to understand the context and what is being maximized or minimized.
The concept that the maximum or minimum can be found by setting the derivative to zero and also considering the endpoints of the domain.
For the company growth problem, the maximum number of employees is predicted to be 168 in the year 2019.
A farmer needs to minimize the cost of fencing a rectangular pasture with a given area, using different costs for different fence types.
The dimensions of the pasture that minimize cost are calculated to be 800 by 200 feet.
The cost function for the farmer's problem is derived from the cost of materials and the area constraint of the pasture.
In a production run problem, the total cost of production and storage is minimized by determining the optimal number of items per run.
The total cost function is a sum of production costs (fixed preparation costs and variable costs per item) and storage costs.
The optimal number of items per production run that minimizes costs is calculated to be 40,000 items.
The use of the second derivative test to confirm that the calculated number of items per run is indeed a minimum.
The problem-solving approach emphasizes breaking down information step by step, similar to taking small bites when eating.
The transcript provides a detailed walkthrough of setting up and solving optimization problems using calculus.
The application of derivatives in real-world scenarios such as business growth, farming, and production runs is explored.
The importance of understanding the context and constraints of a problem before applying mathematical solutions is highlighted.
The process of converting a multi-variable cost function into a single-variable function by using constraints is demonstrated.
The transcript concludes with a reminder to include units when reporting the results of application problems.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: