Optimization Problem Examples
TLDRThe video script is an educational walkthrough on how to solve two economic problems related to maximizing profit for a firm. The first problem involves a firm with a production limit and given cost and revenue functions. The presenter guides viewers on how to derive the profit function, find its critical points through differentiation, and confirm these points as maximum profit points using the number line test. The second problem deals with a firm's weekly demand function and average cost of production. The process is similar, involving the creation of a profit function, differentiation, and solving for critical points to find the quantity that maximizes profit, as well as calculating the selling price per unit and the actual maximum profit. The script emphasizes the importance of understanding the revenue and cost functions, applying mathematical techniques to find maximum profit, and verifying the results. The presenter encourages viewers to rewatch the video for clarification and to ask further questions if needed.
Takeaways
- 📚 First, always read through the problem carefully to understand what is being asked, such as finding the maximum profit.
- 📈 To find a maximum or minimum value, such as profit, you need to derive the function and find its critical points.
- 🔍 Identify the revenue and cost functions from the problem statement, as these are essential for creating the profit function.
- 🧮 The profit function is calculated by subtracting the cost function from the revenue function.
- ✅ Simplify the profit function by combining like terms to prepare it for derivation.
- 📌 Take the derivative of the profit function to find the critical points where the profit is maximized or minimized.
- 🔢 Set the derivative equal to zero and solve for the variable (x) to find the critical points.
- 📉 Use the number line test or a graph to verify that the critical point represents a maximum or minimum.
- 💡 Plug the critical point value back into the original profit function to find the maximum profit.
- 🔄 For problems where revenue and cost functions are not directly given, you may need to derive them from the demand function and other given information.
- 📝 When asked for the selling price, use the demand function to find the price per unit at the quantity that maximizes profit.
- 📉 Always check your work by plugging the values back into the original functions to ensure accuracy.
Q & A
What is the main objective of the problem discussed in the transcript?
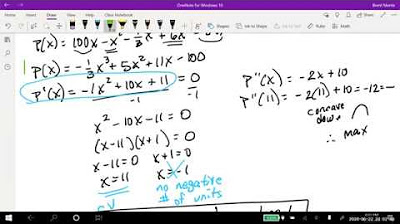
-The main objective is to find the number of units (x) a firm should produce for maximum profit, given the total cost and total revenue functions.
How is profit calculated in the context of the problem?
-Profit is calculated as the difference between total revenue and total cost, which is expressed as Profit = Revenue - Cost.
What is the formula for the total cost given in the transcript?
-The total cost is given by the formula C = 400 + 2x, where x is the number of units produced.
What is the formula for the total revenue given in the transcript?
-The total revenue is given by the formula R = 350x - (1/100)x^2, where x is the number of units produced.
What is the significance of finding the derivative of the profit function?
-The derivative of the profit function helps identify the critical points where the profit could be maximized or minimized. Setting the derivative to zero and solving for x gives potential points for maximum profit.
How does one determine if a critical point is a maximum or minimum?
-One can determine if a critical point is a maximum or minimum by using the second derivative test or by analyzing the sign of the first derivative on either side of the critical point.
What is the maximum number of units the firm should produce according to the transcript?
-The firm should produce 7,500 units to achieve maximum profit.
What is the maximum profit the firm can achieve according to the transcript?
-The maximum profit the firm can achieve is $562,100.
What is the demand function given for the second problem in the transcript?
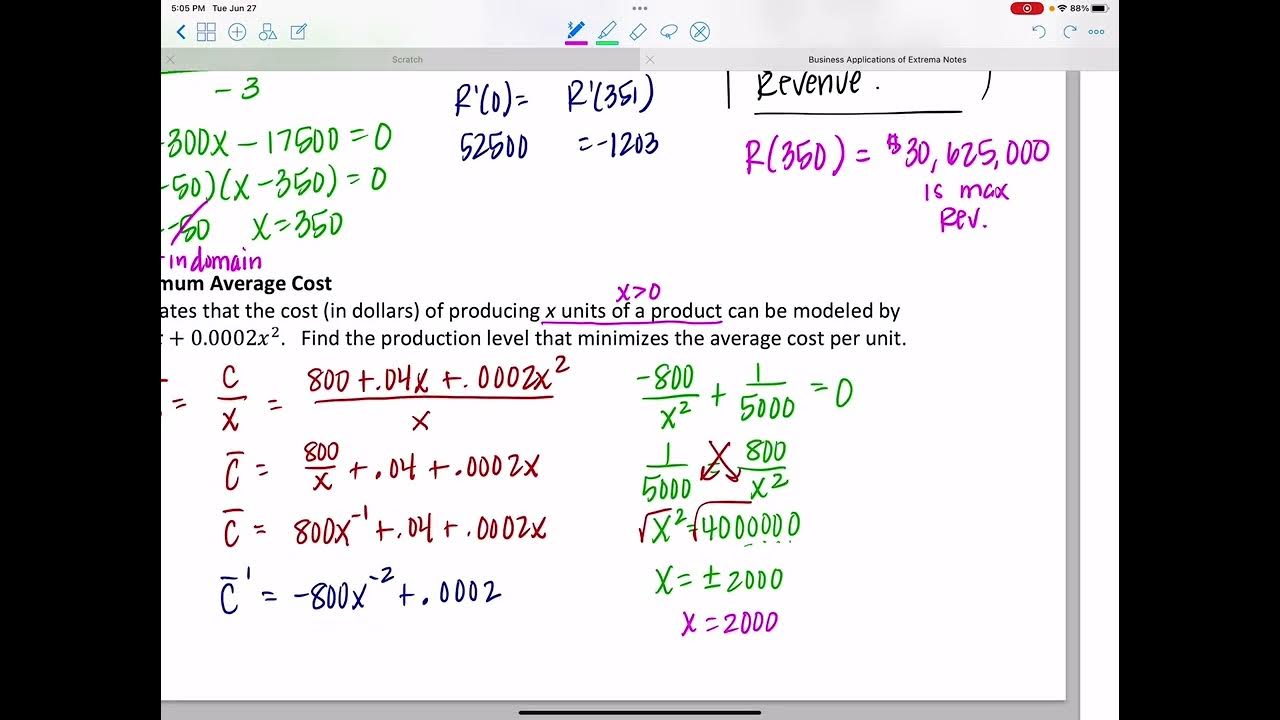
-The demand function for the second problem is P = 800 - (1/2)x, where P is the price and x is the quantity of units sold.
What is the average cost of production and sale given in the second problem?
-The average cost of production and sale is given by the formula C̄ = 400 + 2x, where x is the number of units produced.
How is the revenue calculated in the second problem?
-Revenue is calculated as the price per unit (from the demand function) times the number of units sold (x), so it's (800 - (1/2)x) * x.
What is the quantity that will maximize profit in the second problem?
-The quantity that will maximize profit in the second problem is 80 units.
What is the selling price per unit when the quantity is maximized to 80 units?
-The selling price per unit when the quantity is maximized to 80 units is $760.
What is the actual maximum profit when the quantity is maximized to 80 units?
-The actual maximum profit when the quantity is maximized to 80 units is $16,000.
Outlines
📚 Maximum Profit Calculation for a Firm
This paragraph introduces a problem concerning a firm's production and profit maximization. The firm can produce up to 2,000 units per month, with costs and revenues given by specific functions of the number of units produced (x). The presenter walks through the process of finding the profit function by subtracting the cost function from the revenue function. They then find the derivative of the profit function to locate the critical points, which are potential maxima or minima of profit. By setting the derivative to zero and solving for x, they identify the production quantity that would yield the maximum profit. The presenter also discusses the need to test the critical point to confirm it's a maximum, which can be done through a number line test or by analyzing the sign of the derivative on either side of the critical point.
📈 Determining Optimal Production Quantity and Profit
The second paragraph continues the discussion on profit maximization but focuses on a different scenario. It involves a firm with a given weekly demand function and average cost of production. The presenter explains how to construct the profit function by multiplying the price per unit (from the demand function) by the number of units sold, and then subtracting the total cost. The profit function is then simplified and its derivative is taken to find the critical points. By setting the derivative to zero and solving for x, the presenter identifies the quantity that maximizes profit. They also show how to find the selling price per unit by substituting the optimal quantity into the demand function and calculate the maximum profit by substituting the optimal quantity into the profit function.
🔢 Profit Function and Derivative for a Production Scenario
This paragraph delves into the specifics of constructing a profit function for a production scenario. The presenter begins by outlining the need to multiply the price per unit by the number of units sold to get revenue, and then subtracting the cost per unit times the number of units made to get profit. They then distribute and combine like terms to simplify the profit function. After deriving the profit function, the presenter finds its critical points by setting the derivative to zero and solving for x. They confirm the critical point as a maximum by discussing the change in the sign of the derivative on either side of the critical point. The presenter then provides the quantity that maximizes profit and the corresponding selling price per unit, and shows how to calculate the maximum profit by substituting the optimal quantity back into the profit function.
💡 Summary of Profit Function Calculations
The final paragraph summarizes the process of calculating profit functions and emphasizes two different methods presented in the video. The first method involves directly given revenue and cost functions, while the second requires deriving these functions from a demand function and average cost. The presenter encourages viewers to pause and rewatch parts of the video if needed and to ask any further questions. They also provide a final calculation for the maximum profit by plugging the optimal quantity into the profit function.
Mindmap
Keywords
💡Profit Function
💡Derivative
💡Critical Points
💡Revenue Function
💡Cost Function
💡Maximum Profit
💡Demand Function
💡Average Cost
💡Number Line Test
💡Revenue Minus Cost
💡Quantity to Maximize Profit
Highlights
The transcript discusses how to approach solving problems involving profit maximization for a firm.
The importance of understanding the concept of maximum profit and its relation to the profit function is emphasized.
A step-by-step method is provided for deriving the profit function from given cost and revenue functions.
The process of simplifying the profit function by combining like terms is demonstrated.
The use of derivatives to find critical points for maximizing profit is explained.
A practical example is given to illustrate how to set the derivative equal to zero and solve for the critical point.
The concept of testing critical points using a number line test to confirm a maximum is introduced.
The transcript shows how to calculate the quantity that should be produced for maximum profit.
It is demonstrated how to find the maximum profit by plugging the critical point value into the original profit function.
The transcript covers a second problem involving a demand function and average cost to find the quantity that maximizes profit.
The process of breaking down revenue and cost components from given functions is explained in detail.
The calculation of the selling price per unit based on the demand function is demonstrated.
The final profit is calculated by substituting the quantity that maximizes profit back into the profit function.
The video emphasizes the importance of understanding the relationship between price per item, number of items sold, and cost per item.
The transcript provides a clear example of how to multiply and distribute terms in a profit function.
The process of combining like terms in the profit function to simplify the equation is shown.
The transcript illustrates how to use the derivative of the profit function to find the critical points for profit maximization.
The concept of assuming a critical point maximizes profit is addressed, with a suggestion to use a number line for verification.
The video concludes with an encouragement to pause and re-watch for clarification and to ask further questions if needed.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: