Marginal Revenue, Average Cost, Profit, Price & Demand Function - Calculus
TLDRThe video script delves into the intricacies of economic principles such as marginal cost, revenue, and profit, focusing on how to determine the optimal production level for a business to minimize average costs and maximize profit. It introduces the cost function and explains the calculation of average cost and marginal cost. The script then illustrates how to find the production level that minimizes average cost by equating the average cost function with the marginal cost or by finding the first derivative of the average cost function and setting it to zero. The concept of price function or demand function is introduced, highlighting the inverse relationship between supply (x) and price. The revenue function is explained as the product of the number of units sold and the price per unit. Profit is defined as the difference between revenue and cost. The video also covers how to calculate the production level that maximizes profit by setting the marginal revenue equal to the marginal cost or by finding the first derivative of the profit function and solving for x. The script provides step-by-step examples to calculate costs, average cost, marginal cost, and to determine the production levels for minimum average cost and maximum profit, using different cost and demand functions.
Takeaways
- 📈 The cost function (C(x)) represents the total cost to produce x number of items, and the average cost (AC) is calculated by dividing the total cost by the number of items (x).
- 🔄 Marginal cost (MC) is the first derivative of the cost function and represents the cost of producing one additional unit.
- ⚖️ To minimize the average cost per unit, you should produce the quantity where the average cost function equals the marginal cost.
- 📌 The first derivative of the average cost function, set to zero, can also be used to find the production level that minimizes average cost.
- 💰 The revenue function (R(x)) is calculated by multiplying the number of units sold (x) by the price function (P(x)) which represents the price per unit.
- 📉 The price function typically decreases as the number of units (x) increases, reflecting the principle of supply and demand.
- 🤝 Profit is calculated as revenue minus cost. To maximize profit, set the first derivative of the profit function to zero or equate marginal revenue to marginal cost.
- 🔧 To find the production level that maximizes profit, you can use the profit function or the revenue and cost functions to find the critical points where marginal profit is zero.
- 📊 At the point of minimum average cost, the average cost function is equal to the marginal cost function, which can guide production levels to minimize costs.
- 🔹 If the average cost exceeds the marginal cost, you should increase production. If the average cost is less than the marginal cost, you should decrease production to minimize average costs.
- 💡 The concepts of marginal cost, average cost, revenue, and profit are essential for making economic decisions regarding production levels and pricing strategies.
Q & A
What does the cost function (c of x) represent?
-The cost function (c of x) represents the total cost to produce x number of items.
How is the average cost calculated?
-The average cost is calculated by dividing the cost function by the number of items (x).
What is the marginal cost?
-The marginal cost is the first derivative of the cost function, representing the cost of producing one additional unit.
What does the marginal cost tell you in a real-life example?
-The marginal cost tells you how much extra it will cost to produce one more unit of a product.
How can you find the production level that minimizes the average cost?
-You can find the production level that minimizes the average cost by setting the average cost function equal to the marginal cost and solving for x, or by finding the first derivative of the average cost function, setting it to zero, and solving for x.
What is the relationship between the average cost and marginal cost functions in determining the minimum average cost?
-The average cost will be at a minimum whenever the average cost function is equal to the marginal cost function.
What is the revenue function (r of x)?
-The revenue function (r of x) is the product of the number of units sold (x) and the price function (p of x), representing the total revenue from selling x units.
How is profit calculated?
-Profit is calculated as the difference between the revenue and the cost, or as the revenue per unit minus the cost per unit, multiplied by the number of units sold.
What is marginal profit?
-Marginal profit is the first derivative of the profit function, which is equal to the marginal revenue minus the marginal cost.
How can you find the production level that maximizes profit?
-You can find the production level that maximizes profit by setting the marginal profit to zero and solving for x, or by setting the marginal revenue equal to the marginal cost and solving for x.
What is the significance of setting marginal revenue equal to marginal cost to maximize profit?
-Setting marginal revenue equal to marginal cost ensures that the additional revenue gained from selling one more unit is exactly balanced by the additional cost of producing that unit, which is the point at which profit is maximized.
Outlines
📊 Introduction to Cost Functions and Minimizing Average Cost
The video begins by focusing on economic problems such as marginal cost, revenue, and profit. It introduces the cost function (c(x)) as the total cost to produce 'x' items. The average cost is then defined as the cost function divided by 'x'. The concept of marginal cost as the first derivative of the cost function is also explained. The video aims to help viewers understand how to find the optimal number of units to produce to minimize the average cost per unit, which is crucial for business efficiency and profitability.
🔍 Calculating Average and Marginal Costs for 100 Units
The script provides a detailed example to illustrate the calculation of average and marginal costs. Given a cost function c(x) = 5000 + 15x + 0.01x^2, the total cost to produce 100 units is calculated, resulting in $6600. The average cost per unit is then determined by dividing the total cost by the number of units, yielding an average cost of $66 per unit. The marginal cost function is derived and used to calculate the additional cost of producing one more unit beyond 100, which is found to be approximately $17 per unit.
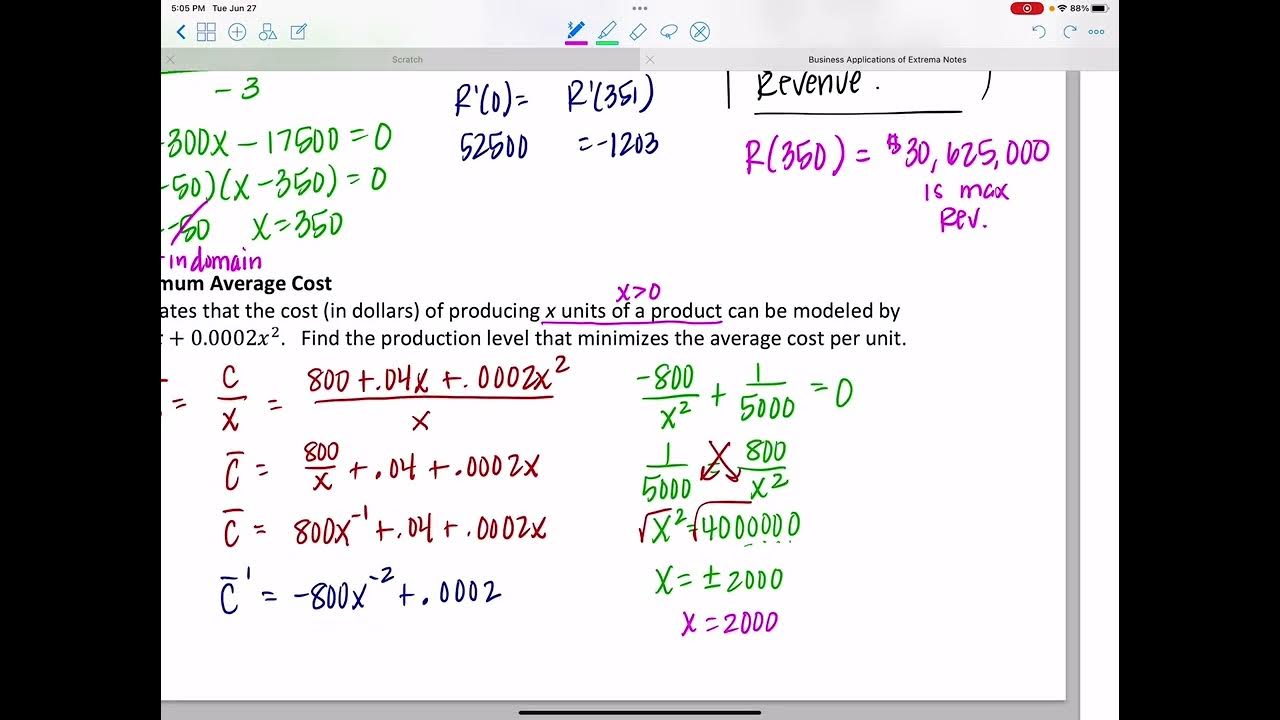
🔢 Finding the Production Level to Minimize Average Costs
The video explains how to find the production level that minimizes the average cost. It is shown that the average cost is minimized when the average cost function is equal to the marginal cost. The script guides viewers through setting these two functions equal to each other and solving for 'x'. Using the cost function from the previous example, the minimum average cost is found to occur at a production level of 707 units, with a minimum average cost of $29.14 per unit.
📈 Comparing Average Costs at Different Production Levels
To validate the minimum average cost, the video compares the average cost per unit at different production levels. It shows that the average cost at 100 units is $66, and it is higher at 600 units ($29.33) and 800 units ($29.25) compared to the minimum average cost at 707 units ($29.14). This comparison confirms that producing 707 units results in the lowest average cost, which is essential for maximizing profit.
📉 Cost Function with a New Example and Minimizing Average Cost
The video presents a new cost function, c(x) = 30,000 + 200x + 0.1x^2, and repeats the process of finding the cost, average cost, and marginal cost for producing 100 units. The total cost for 100 units is calculated to be $51,000, resulting in an average cost of $510 per unit. The marginal cost at 100 units is determined to be $220 per unit. The video encourages viewers to practice by finding the production level that minimizes the average cost and calculating the minimum average cost for this new function.
🔧 Setting Marginal Cost Equal to Average Cost to Minimize It
The script explains the process of setting the marginal cost equal to the average cost to find the production level that minimizes the average cost. By solving the equation 0.1x = 30,000/x, the optimal production level is found to be 548 units. The minimum average cost at this production level is calculated to be $309.54 per unit. The video also demonstrates an alternative method of finding the minimum average cost by taking the derivative of the average cost function and setting it to zero.
📊 Analyzing Average and Marginal Costs at Different Production Levels
The video analyzes the relationship between average cost, marginal cost, and production levels. It shows that at a production level of 100 units, the average cost is $510, and at 548 units, it is minimized at $309.54. At 1000 units, the average cost increases slightly to $330. The marginal cost is calculated at different production levels, and it is observed that at the minimum average cost, the average cost function equals the marginal cost. The video explains that comparing the average cost to the marginal cost can indicate whether to increase or decrease production to minimize the average cost.
📈 Price Function and the Impact of Supply on Demand
The video introduces the price function (p(x)) or demand function, which represents the price per unit that a company can charge for selling 'x' units. It explains the inverse relationship between supply (x) and demand, where an increase in supply leads to a decrease in demand and price, and vice versa. Examples of calculators and diamonds are used to illustrate this concept. The video emphasizes the importance of understanding the relationship between supply, demand, and price.
💰 Revenue Function and the Calculation of Profit
The script defines the revenue function (r(x)) as the product of the number of units sold (x) and the price function (p(x)). It provides examples to illustrate how revenue is calculated and relates it to the concept of profit, which is the difference between revenue and cost. The video explains that to maximize profit, one must consider both revenue and cost, and it introduces the profit function (P(x)) as revenue minus cost. It also touches on the concept of marginal profit as the first derivative of the profit function.
🤑 Maximizing Profit by Balancing Revenue and Cost
The video concludes with examples of how to find the production level that maximizes profit. Given cost and demand functions, it shows how to calculate the revenue function, find the profit function, and then determine the production level at which profit is maximized. The process involves setting the first derivative of the profit function to zero and solving for 'x', or alternatively, setting the marginal revenue equal to the marginal cost and solving for 'x'. The video provides calculations for a scenario with a constant price function and another with a variable price function, demonstrating how to find the production level and maximum profit in each case.
🎬 Conclusion and Final Thoughts on Maximizing Profit
The video wraps up by summarizing the process for finding the production level that maximizes profit and calculating the maximum profit. It emphasizes the importance of understanding cost functions, revenue functions, and the relationship between marginal revenue and marginal cost. The video thanks viewers for watching and encourages them to apply these concepts to real-world business scenarios.
Mindmap
Keywords
💡Cost Function
💡Average Cost
💡Marginal Cost
💡Production Level
💡Revenue Function
💡Profit
💡Marginal Profit
💡Price Function
💡Demand Function
💡Marginal Revenue
💡First Derivative
Highlights
The video discusses the concept of marginal cost, revenue, and profit, focusing on how to calculate them and use them to determine optimal production levels.
The cost function (c of x) represents the total cost to produce x number of items, with average cost being the cost function divided by x.
Marginal cost is the first derivative of the cost function, indicating the cost of producing one additional unit.
To minimize the average cost per unit, the average cost function should be equal to the marginal cost.
The minimum average cost can be found by either setting the average cost equal to the marginal cost or by finding the first derivative of the average cost function and solving for x.
The cost to produce 100 units is calculated using the given cost function, resulting in a total cost of $6600.
The average cost to produce a single unit is $66 when producing 100 units.
The marginal cost at 100 units is $17 per unit, meaning the total cost increases by approximately $17 to produce one extra unit.
The production level that minimizes the average cost is found to be 707 units, with a minimum average cost of $29.14 per unit.
The video demonstrates how to prove the minimum average cost by comparing it with costs at different production levels, such as 600 and 800 units.
The price function (p of x), or demand function, represents the price per unit the company can charge for x units, with price typically decreasing as the number of units (supply) increases.
Revenue is calculated as the number of units sold (x) times the price function (p of x), showing the total income from sales.
Profit is the difference between revenue and cost, and can be maximized by setting the marginal revenue equal to the marginal cost.
The video provides a step-by-step example of finding the production level that maximizes profit, using both the profit function and the revenue and cost functions.
The maximum profit can be found by plugging the optimal production level back into the profit function.
The video concludes with a summary of how to use average cost, marginal cost, and price functions to determine production levels for minimum average cost and maximum profit.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: