Special Relativity | Lecture 8
TLDRThe video script is a detailed lecture on the fundamentals of electromagnetism, specifically focusing on Maxwell's equations and the concept of relativity. The lecturer begins by discussing the historical context of Einstein's work on the electrodynamics of moving objects and its connection to the transformation properties of the electromagnetic field tensor. The script delves into the mathematical representation of electric and magnetic fields, introducing the electromagnetic field tensor, and explores its transformation properties under different frames of reference. Key identities in vector calculus are highlighted, leading to the derivation of half of Maxwell's equations directly from the definitions of the fields in terms of the vector potential. The remaining equations are discussed in the context of charge density and current density, with an emphasis on their role in the conservation of charge. The lecture concludes with an exploration of the relativistic notation of Maxwell's equations, aiming to express them as tensor equations invariant under Lorentz transformations. The script is rich in physics, providing a deep understanding of the subject matter.
Takeaways
- 📚 The lecturer begins by discussing the transformation properties of the electromagnetic field tensor, which is deeply connected to Einstein's first paper on the electrodynamics of moving objects.
- 🧲 Einstein was particularly interested in the invariance of electromagnetic phenomena and how different reference frames could attribute effects to either magnetic or electric fields.
- 💡 The lecturer emphasizes the importance of understanding the transformation from one frame to another, which is crucial for grasping the concept of relativity.
- 📐 The electromagnetic field tensor is introduced as an anti-symmetric tensor with two indices, which can be expressed in terms of the vector potential.
- 🔋 The magnetic field is shown to be related to the space components of the tensor, and the electric field to the mixed space-time components.
- 🌀 The lecturer explains that the curl of the electric field and the time derivative of the magnetic field are related, which is a part of Maxwell's equations.
- 🚀 The concept of charge density (ρ) and current density (J) are defined in the context of Maxwell's equations, with ρ representing the amount of charge per unit volume and J representing the flow of charge.
- 🔗 The lecturer discusses the importance of charge conservation, which is a fundamental principle stating that the total charge in a closed system remains constant.
- ⚙️ Maxwell's equations are shown to be expressible in a relativistic notation, suggesting that E and B fields form an anti-symmetric tensor, while ρ and J form a four-vector.
- 🔍 The Bianchi identity is introduced as a tensor equation that is a consequence of the definitions of the electromagnetic field in terms of the vector potential.
- 📉 The lecturer touches on the concept of magnetic monopoles and hints at discussing them later, noting the current lack of empirical evidence for their existence.
Q & A
What is the main topic of discussion in the provided transcript?
-The main topic of discussion is the exploration of the electromagnetic field tensor, its transformation properties, and the connection to Einstein's paper on the electrodynamics of moving objects. The lecturer also delves into Maxwell's equations and their implications in the context of special relativity.
Why did the lecturer refer to Einstein's first paper?
-The lecturer referred to Einstein's first paper to highlight the puzzle of the invariance of certain electromagnetic phenomena across different reference frames, which is deeply connected to the transformation properties of the electromagnetic field tensor.
What is the significance of the electromagnetic field tensor in the context of this discussion?
-The electromagnetic field tensor is significant because it encapsulates the electric and magnetic fields and their transformation properties under different reference frames. It is central to understanding how these fields appear in different ways depending on the observer's motion.
What is the Lorentz transformation?
-The Lorentz transformation is a set of mathematical equations that describe how quantities such as space and time measurements are altered for observers in relative motion. In the context of this transcript, it is used to understand the transformation of electric and magnetic fields between different inertial frames.
Why is the concept of 'charge conservation' important in the context of Maxwell's equations?
-Charge conservation is important because it is a fundamental law of physics stating that the total electric charge in a closed system remains constant over time. It is intrinsically linked to the continuity equation, which is derived from Maxwell's equations and ensures that any change in charge density within a region is due to the flow of charge through the boundary of that region.
What are the two types of Maxwell's equations discussed in the transcript?
-The two types of Maxwell's equations discussed are: 1) those that come for free, which are identities following from the definitions of the electric and magnetic fields in terms of the vector potential, and 2) those derived from an action principle, which are dynamical and not purely definitional.
What is the role of the vector potential in defining the electric and magnetic fields?
-The vector potential plays a crucial role in defining the electric and magnetic fields through its space and time derivatives. The electric field is given by the time derivative of the vector potential, while the magnetic field is related to the space components of the curl of the vector potential.
How does the lecturer connect the concept of a moving magnet and a wire to the discussion of electric and magnetic fields?
-The lecturer uses the example of a moving magnet and a wire to illustrate the relativity of descriptions of electromagnetic phenomena. A moving magnet induces an electric field in the wire, which exerts a force on the electrons within it. Conversely, a moving wire in a magnetic field experiences a force due to the magnetic field on the moving electrons. This demonstrates how what appears as a magnetic field in one frame can appear as an electric field in another.
What is the Bianchi identity mentioned in the transcript?
-The Bianchi identity is a set of equations that are a special case of identities in the theory of tensors. In the context of the electromagnetic field tensor, it expresses the fact that the magnetic field has no divergence, which implies the non-existence of magnetic charge densities or magnetic currents in the context of classical electromagnetism.
How does the lecturer explain the transformation of the electromagnetic field tensor under a change of reference frame?
-The lecturer explains that the electromagnetic field tensor, which contains the electric and magnetic fields, transforms under a change of reference frame according to the rules for tensor transformation. This transformation is achieved by applying the Lorentz transformation matrix to the tensor components, which allows one to determine the new components of the electromagnetic field in the moving frame.
What is the significance of the absence of magnetic monopoles in the context of the lecture?
-The absence of magnetic monopoles is significant because it implies that the magnetic field has no sources or divergence, a fact that is reflected in one of Maxwell's equations. The lecturer mentions that the non-existence of magnetic monopoles is consistent with the Bianchi identity and the overall structure of Maxwell's equations.
Outlines
📘 Introduction to Electromagnetic Fields and Einstein's Paper
The lecturer begins by expressing the intention to discuss the dynamics of electric and magnetic fields, specifically the field equations and their relation to charges. The conversation diverts to a historical account, mentioning a visit to Belgium and the experience of reading Einstein's first paper on the electrodynamics of moving objects. The paper's introduction is highlighted for its clarity in expressing Einstein's motivation, which is linked to the transformation properties of the electromagnetic field tensor. The lecturer suggests that the paper is worth reading for its historical and scientific significance.
🧲 Magnetic Fields, Charged Particles, and Einstein's Thought Process
The summary delves into the effects of magnetic fields on charged particles, referencing Einstein's contemplations on the forces involved when a charged particle moves through a magnetic field. It discusses the scenario of a particle moving along the x-axis under the influence of a magnetic field and the resulting force, known as the Lawrence force. The lecturer then contrasts this with the perspective of a moving magnet creating an electric field, emphasizing Einstein's insight that these seemingly different phenomena are fundamentally the same, leading to the concept of electric and magnetic fields being interconnected and transforming into each other under different frames of reference.
🔍 Exploring the Electromagnetic Field Tensor's Transformation Properties
This section focuses on the mathematical representation of the electromagnetic field tensor, its anti-symmetric nature, and its components related to electric and magnetic fields. The lecturer outlines the tensor's relationship with the vector potential and how the magnetic field is associated with the curl of the vector potential. A comprehensive matrix representation of the tensor is provided, highlighting the spatial and temporal components, and the lecturer emphasizes the need to understand how this tensor transforms under different frames of reference.
📐 Lorentz Transformation and Tensors
The lecturer introduces the concept of Lorentz transformation, which is key to understanding how tensors, specifically the electromagnetic field tensor, transform between different frames of reference. The transformation rules for scalars, vectors, and tensors with indices are discussed. The Lorentz transformation matrix is derived and its components are explained in relation to the velocity of the moving frame. The goal is to apply these rules to find the new components of the electromagnetic field tensor in a frame moving along the x-axis.
🌀 Maxwell's Equations and Their Implications
The lecturer outlines Maxwell's equations, emphasizing that half of them are identities following from the definitions of electric and magnetic fields in terms of the vector potential. The divergence of the magnetic field is shown to be zero, implying the non-existence of magnetic monopoles. The time derivative of the magnetic field is related to the electric field, leading to another Maxwell equation. The lecturer also touches on the concept of charge density and current, which are key to the remaining Maxwell equations that are not identities and are derived from an action principle.
🔋 Charge Density, Current Density, and Their Role in Maxwell's Equations
The concept of charge density (ρ) and current density (J) are explained in detail. Charge density is defined as the total charge within a volume divided by that volume, while current density is described as the amount of charge per unit area per unit time. The lecturer emphasizes the importance of these quantities in the context of Maxwell's equations, particularly in the conservation of charge. The idea that charge can only change within a region if it passes through the boundaries of that region is highlighted, leading to the local conservation of charge, which is a direct consequence of Maxwell's equations.
🔗 Relativistic Notation of Maxwell's Equations
The lecturer aims to express Maxwell's equations in a relativistic notation to demonstrate their invariance under Lorentz transformations. The components of the electromagnetic field tensor (E and B) and the four-vector (ρ and J) are identified as key elements in this expression. The lecturer suggests that the set of four equations can be written in a tensor form that is invariant under Lorentz transformations, thus maintaining the symmetry between space and time. The challenge is to rewrite these equations in a way that clearly shows this invariance.
🧵 The Bianchi Identity and the Absence of Magnetic Charges
The lecturer concludes with a discussion on the Bianchi identity, a tensor equation that is a special case of an identity in general relativity. It is shown that the Bianchi identity, which is equivalent to certain Maxwell's equations, implies that the magnetic field has no divergence, and by extension, there are no magnetic charge densities or currents. The lecturer invites the audience to explore the Bianchi identity further and to understand its geometric meaning and implications in the context of electromagnetism.
Mindmap
Keywords
💡Maxwell's equations
💡Electromagnetic field tensor
💡Lorentz transformation
💡Charge density
💡Current density
💡Bianchi identity
💡Curl
💡Divergence
💡Vector potential
💡Action principle
💡Relativistic notation
Highlights
The lecturer begins by discussing the dynamics of electric and magnetic fields, emphasizing the importance of understanding the transformation properties of the electromagnetic field tensor.
A historical perspective is provided on Einstein's first paper, highlighting his motivation and logic behind the study of the electrodynamics of moving objects.
The puzzle of the invariance of certain electromagnetic phenomena across different reference frames is explored, which is central to the concept of relativity.
Einstein's realization that electric and magnetic fields are part of a complex that transforms into each other under certain conditions is discussed.
The concept of the electromagnetic field tensor Fμν is introduced, with an explanation of its anti-symmetric properties and its relation to electric and magnetic fields.
The lecturer explains how a magnetic field in one reference frame can appear as an electric field in another, moving frame of reference.
The transformation properties of the electromagnetic field tensor are detailed mathematically, showing how a moving observer can perceive an electric field where there was only a magnetic field in the stationary frame.
The Lorentz transformation rules for tensors are outlined, showing how the components of the electromagnetic field tensor transform when moving between reference frames.
The derivation of the existence of an electric field in a moving frame of reference, starting with only a magnetic field present in the stationary frame, is demonstrated.
Maxwell's equations are introduced, with the lecturer noting that half of them are identities following from the definitions of electric and magnetic fields in terms of the vector potential.
The讲师 explains the concept of charge density (ρ) and current density (J), which are key to the remaining Maxwell's equations that are not identities.
The importance of charge conservation is discussed, and it is shown how this principle is inherently included in Maxwell's equations through the work of Maxwell.
The lecturer presents the local conservation of charge, also known as the continuity equation, which is a direct consequence of Maxwell's equations.
The possibility of expressing Maxwell's equations in a relativistic notation that makes them invariant under Lorentz transformations is explored.
The Bianchi identity, a tensor equation that is a special case of a more general identity in general relativity, is introduced as a way to express certain Maxwell's equations in a covariant form.
The lecturer concludes with a teaser for the next lecture, where the action principle derivation of the remaining Maxwell's equations will be covered.
Transcripts
Browse More Related Video

Lecture 7 | Quantum Entanglements, Part 3 (Stanford)
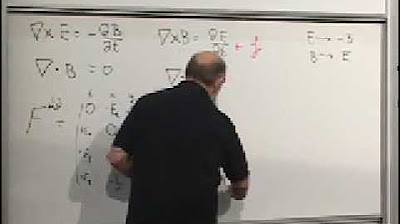
Lectures 2 & 3 | Quantum Entanglements, Part 3 (Stanford)

Maxwell's Equations Explained: Supplement to the History of Maxwell's Eq.

Special Relativity | Lecture 6

Special Relativity | Lecture 4

The Electromagnetic field, how Electric and Magnetic forces arise
5.0 / 5 (0 votes)
Thanks for rating: