Maxwell's Equations Explained: Supplement to the History of Maxwell's Eq.
TLDRThe video script offers an in-depth exploration of Maxwell's equations, which are fundamental to understanding electromagnetism. It begins with an introduction to vectors and vector multiplication, explaining the difference between scalars, which have only magnitude, and vectors, which have both magnitude and direction. The script then delves into the dot and cross products, using physical examples like force and distance to illustrate the concepts. Maxwell's equations are explained in detail, starting with the divergence, which measures how a vector field spreads out or converges at a point, and Gauss's law, which relates the electric flux through a closed surface to the charge enclosed. The script also covers the curl, which measures the rotation of a vector field around a point, and Faraday's law of electromagnetic induction, which describes how a changing magnetic field can induce an electric field. The final part of the script discusses the historical context and implications of Maxwell's work, including its role in the discovery of radio waves and its influence on Einstein's theory of relativity. The summary emphasizes the significance of Maxwell's equations in unifying the concepts of electricity and magnetism and their profound impact on modern physics.
Takeaways
- 🔌 Electricity Basics: Understanding vectors, scalars, and vector multiplication (dot product and cross product).
- 🧮 Vector Definitions: Scalars have value but no direction; vectors have both value and direction.
- ⚖️ Work and Energy: Dot product of force and distance measures work done, producing a scalar value.
- 🔄 Torque and Direction: Cross product of force and distance gives torque, a vector quantity with direction.
- 🔁 Divergence: Divergence measures how much a vector field diverges from a point, crucial in Gauss's law.
- 🌀 Curl: Curl measures how much a vector field curls around a point, integral to understanding Maxwell's equations.
- 🔧 Historical Insights: Discoveries by Coulomb, Faraday, and Ampere laid the groundwork for Maxwell's equations.
- 📚 Maxwell's Equations: Four fundamental equations describe how electric and magnetic fields interact.
- 🌊 Light as Electromagnetic Waves: Maxwell's equations show light is a transverse wave of electric and magnetic fields.
- 📡 Practical Applications: Hertz's discovery of radio waves validated Maxwell's equations, leading to the wireless revolution.
Q & A
What is the fundamental difference between scalars and vectors?
-Scalars have value but no direction, such as mass. Vectors, on the other hand, have both value and direction, like weight which is influenced by gravity.
How can vectors be represented?
-Vectors can be represented by an arrow indicating a specific direction, or by their components in the x, y, and z directions.
What are the two common methods of vector multiplication?
-The two common methods of vector multiplication are the dot product, which multiplies components in the same direction, and the cross product, which multiplies components that are perpendicular.
What is the physical meaning of the dot product between force and distance?
-The dot product between force and distance gives the work done on an object, which is the amount of energy transferred to the object.
What is the result of the cross product between force and distance?
-The cross product between force and distance results in torque, which is a measure of the spinning force with a direction dependent on the rotation.
What is the significance of the DEL function in the context of Maxwell's equations?
-The DEL function is a vector differential operator that has derivatives in each direction. It is used in Maxwell's equations to calculate divergence and curl, which are key to understanding how electric and magnetic fields change over space.
What does the divergence operation represent in the context of electric fields?
-The divergence operation represents how much an electric field changes in all directions as you move away from a point in space.
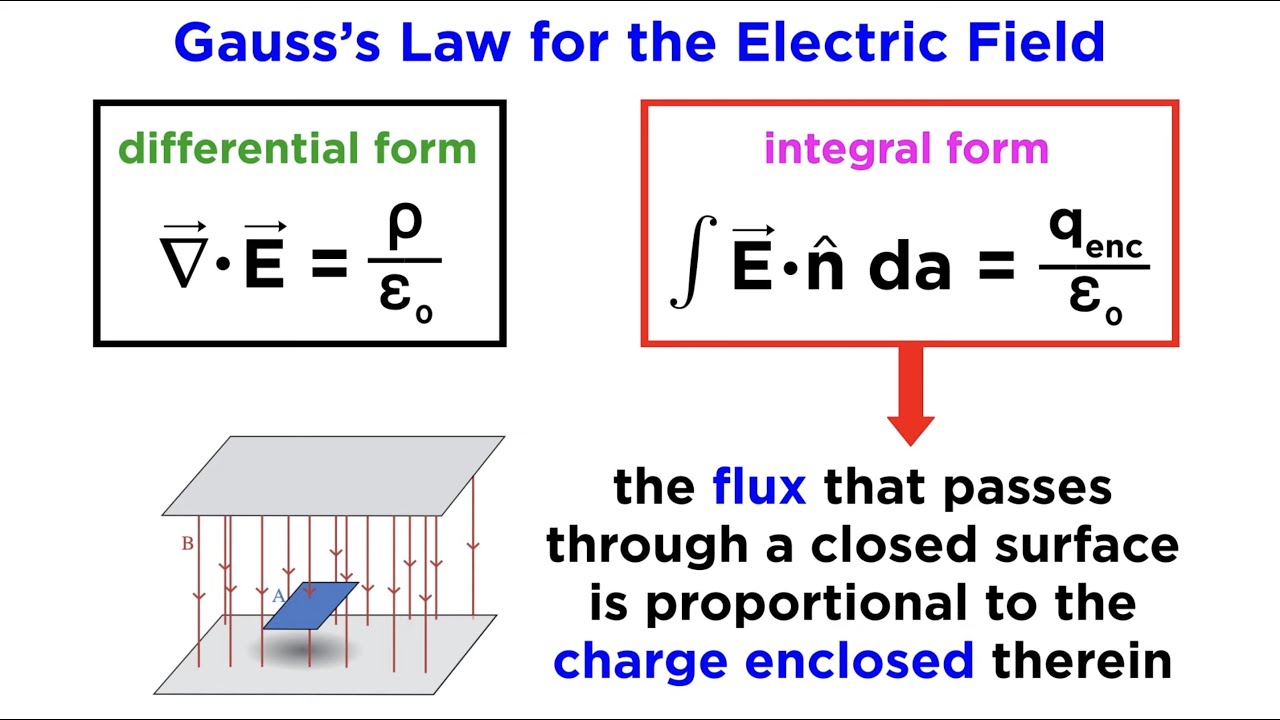
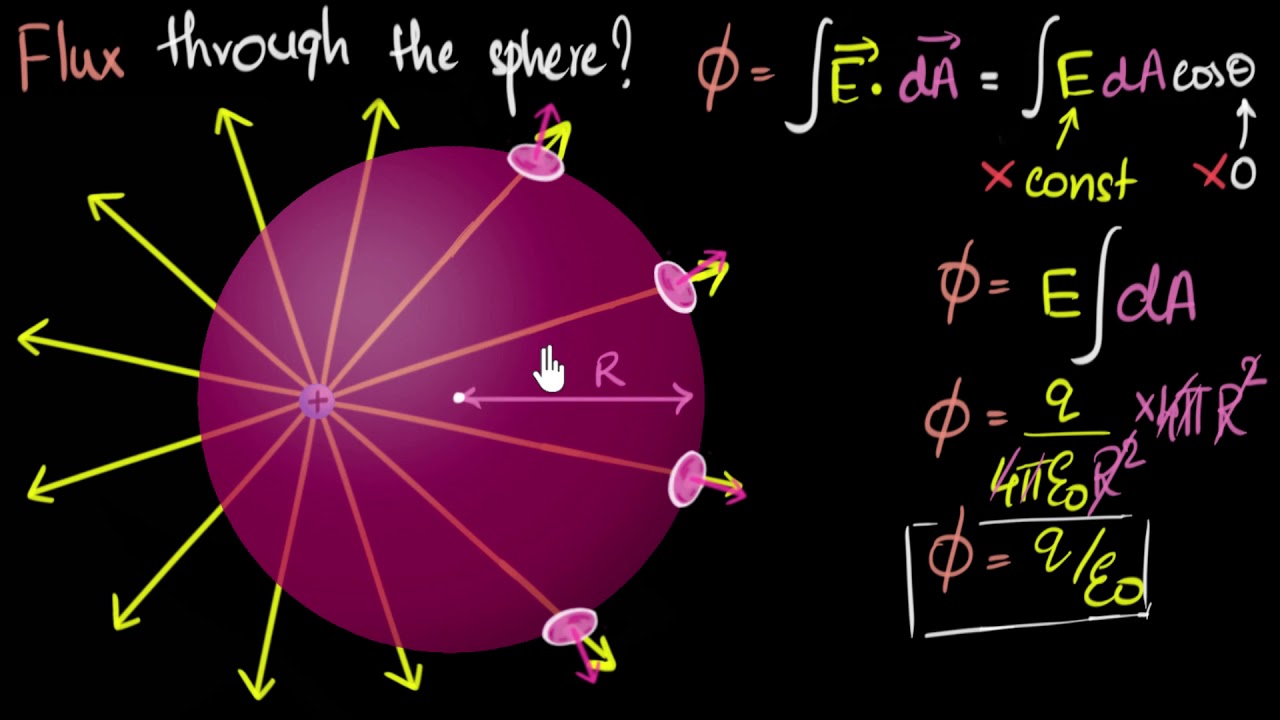
What is Gauss's law and how is it related to electric charges?
-Gauss's law states that the divergence of the electric displacement field D equals the charge density (rho) over the permittivity of free space (epsilon not). It means that the electric field diverges from regions of excess positive charge and converges towards regions of excess negative charge.
Why is the divergence of a magnetic field always zero?
-The divergence of a magnetic field is always zero because magnetic fields cannot converge or diverge from a point. This implies that magnetic field lines are always closed loops with no beginning or end.
What is the physical interpretation of the curl operation in the context of magnetic fields?
-The curl operation measures how much a magnetic field changes as it curls around a point in a circle. It is related to the presence of electric currents or changing electric fields that induce a magnetic field.
How did Maxwell's equations lead to the understanding that light is an electromagnetic wave?
-Maxwell's equations, particularly the curl equations for electric and magnetic fields, showed that a changing magnetic field induces a curling electric field and vice versa. This led Maxwell to infer that light must be a transverse wave of electric and magnetic disturbances, which was later experimentally confirmed by Heinrich Hertz.
What is the historical significance of Ampere's law with Maxwell's addition?
-Ampere's law with Maxwell's addition states that the curl of the magnetic field B is proportional to the electric current density (j) plus the time rate of change of the electric field (epsilon not times the derivative of E with respect to time). This law not only explains how electric currents generate magnetic fields but also how changing electric fields can induce magnetic fields, which is a fundamental concept in electromagnetism and was a stepping stone to understanding electromagnetic waves.
How did Maxwell's equations influence Einstein's theory of relativity?
-Maxwell's equations, especially in conjunction with the principle of relativity, led Einstein to the conclusion that mass is a direct measure of the energy contained in a body, resulting in his famous equation E=mc^2.
Outlines
📚 Basics of Electricity and Vectors
This paragraph introduces fundamental concepts of electricity with a focus on vectors and their multiplication methods, namely the dot product and cross product. It explains that scalars like mass have value but no direction, whereas vectors like weight have both. The paragraph uses the example of force and distance to illustrate how the dot product results in work done (a scalar), while the cross product results in torque (a vector). The importance of the direction in vector operations is highlighted, and a mnemonic for cross product signs is introduced using a triangle of X, Y, and Z.
🔍 Exploring the DEL Function and Gauss's Law
The second paragraph delves into the DEL function, also known as the vector differential operator, which is used to calculate derivatives in multiple directions. It introduces the concepts of divergence and curl in relation to the DEL function. Divergence measures how a vector field spreads out from a point, while curl measures how much it curls around a point. The paragraph connects these concepts to Maxwell's equations, particularly Gauss's law, which relates the divergence of the electric field to the charge density and asserts that the divergence of the magnetic field is always zero, indicating magnetic fields can only form closed loops.
🧲 Maxwell's Equations and the History of Electromagnetism
This paragraph provides a historical context for Maxwell's equations, starting with Coulomb's torsion balance experiment and his discovery of the electric force's dependency on charge size and distance. It discusses Faraday's experiments with conductive cages and his concept of lines of electric and magnetic force. The paragraph then describes Maxwell's approach to modeling these lines of force using the displacement field D and Gauss's method of imaginary closed surfaces. The relationship between the electric field E and the displacement field D is also explained through Maxwell's constant K and the permittivity constant epsilon.
🌀 Ampere's Law and the Concept of Electromagnetic Induction
The fourth paragraph discusses Ampere's law and its extension by Maxwell to include a changing electric field as a source of magnetic field curl. It recounts Ampere's experiments with spirals of wire that acted like magnets and his discovery of the force between two parallel currents. The paragraph also explains Maxwell's hypothesis that a changing electric field induces a magnetic field, which was a key insight leading to the concept of electromagnetic induction. This historical account leads up to Maxwell's formulation of Ampere's law with an additional term accounting for the displacement current.
🌐 The Relationship Between Electricity, Magnetism, and Light
This paragraph explores the implications of Maxwell's equations for the understanding of electromagnetism and light. It describes how Maxwell's laws support the idea that all magnetic fields are due to the action of electric charges, unifying the electric and magnetic forces. The paragraph also discusses the historical significance of Maxwell's work in predicting the existence of electromagnetic waves and their propagation at the speed of light, which was later experimentally confirmed by Heinrich Hertz. The connection between Maxwell's equations and Einstein's mass-energy equivalence principle is highlighted, emphasizing the far-reaching impact of Maxwell's theories.
🚀 The Impact of Maxwell's Laws on Modern Wireless Communication
The final paragraph discusses the practical applications of Maxwell's laws, particularly in the field of wireless communication. It mentions the discovery of radio waves by Heinrich Hertz and how these findings validated Maxwell's laws. The paragraph also touches on the broader impact of Maxwell's work, including its influence on Albert Einstein's theory of relativity and the mass-energy equivalence formula E=mc². The summary concludes with a reference to the importance of Maxwell's laws in the ongoing wireless revolution and their foundational role in modern physics.
Mindmap
Keywords
💡Scalars and Vectors
💡Dot Product
💡Cross Product
💡Del Operator
💡Divergence
💡Gauss's Law
💡Curl
💡Ampere's Law
💡Electromagnetic Induction
💡Maxwell's Equations
Highlights
Introduction to vectors and their properties, including the difference between scalars and vectors.
Explanation of vector representation through magnitude and direction.
Clarification on the concepts of dot product and cross product in vector multiplication.
Illustration of work done and energy transfer using the dot product of force and distance.
Introduction of torque as a result of the cross product between force and distance.
Discussion on the importance of the order of operations in cross product calculations.
Introduction to the DEL function, divergence, and Gauss's law in the context of vector derivatives.
Historical context of Coulomb's and Faraday's experiments leading to Gauss's law.
Maxwell's use of integration by parts to relate electric displacement and charge density.
Explanation of the relationship between electric field E and displacement field D.
Introduction to Ampere's law and its connection to the magnetic field around currents.
Maxwell's addition to Ampere's law to include the effect of changing electric fields.
Faraday's discovery of electromagnetic induction and its relation to changing magnetic fields.
Maxwell's derivation of Faraday's law of induction and its significance.
Maxwell's equations' role in demonstrating that light is an electromagnetic wave.
Hertz's experimental validation of Maxwell's theory of light and the discovery of radio waves.
Einstein's connection of his mass-energy equivalence equation to Maxwell's laws.
The impact of Maxwell's laws on the understanding of electromagnetism and the development of wireless communication.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: