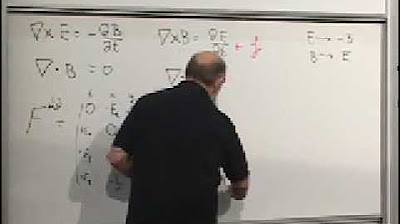Special Relativity | Lecture 4
TLDRThe video script is a detailed lecture on classical field theory, delivered at Stanford University. It begins with an introduction to fields as observable quantities that vary with space and time, using examples like temperature and wind velocity to illustrate scalar and vector fields. The professor then transitions into the mathematical framework of field theory, emphasizing the principle of least action—a fundamental concept in physics that seeks the path of least action in the presence of forces. The lecture explores the Lagrangian formulation, Euler-Lagrange equations, and the importance of constructing an invariant action integral. It also touches upon the distinction between scalar and vector fields and their transformation properties under Lorentz transformations, which are crucial for ensuring the theory's consistency across different reference frames. The script concludes with a discussion on how particles interact with fields, particularly focusing on the concept of mass renormalization in the presence of a scalar field, drawing parallels to the Higgs mechanism in particle physics. The lecture is rich in mathematical derivations and provides a solid foundation for understanding the dynamics of fields and their interaction with particles.
Takeaways
- 📚 The lecture introduces classical field theory, distinct from quantum field theory, focusing on concepts like electromagnetism and the behavior of fields in space-time.
- ⏱️ Space-time is described by one time coordinate and multiple space coordinates, with fields varying across space and time, such as the electric field or temperature.
- 🌡️ Fields can be scalar (like temperature) or vector (like wind velocity), with scalar fields having magnitude and vector fields having both magnitude and direction.
- 📐 The principle of least action is used to describe the motion of particles and is extended to field theory, where the action is minimized over space-time to find the field configuration.
- 🔧 The Euler-Lagrange equations are derived from the action principle and provide the equations of motion for fields, similar to how Newton's equations are derived for particles.
- 🌌 The lecture discusses the transition from particle mechanics to field theory, highlighting that a field can be thought of as a function of time in a space with zero spatial dimensions.
- 🚀 The concept of a Lagrangian density is introduced for field theory, which is a function of the field and its derivatives that is integrated over space-time to obtain the action.
- ⚙️ The Lagrangian for field theory is constructed to be invariant under Lorentz transformations, ensuring that the equations of motion derived from it are consistent across different reference frames.
- 🔥 The potential energy function in the Lagrangian can be thought of as a scalar field that contributes to the field's dynamics, similar to a spring constant in a harmonic oscillator.
- 🤔 The lecture touches on the connection between fields and particles, suggesting how a particle's motion might be influenced by an ambient field, such as the Higgs field in particle physics.
- 🧠 The complexity of the equations of motion for a particle in a field is acknowledged, with the lecturer noting that while not elegant, these equations are crucial for understanding particle-field interactions.
Q & A
What is the main focus of the lecture?
-The lecture primarily focuses on classical field theory, its principles, and the mathematical framework that underpins it. It discusses the concept of fields as observable quantities that vary with space and time, and how these fields can be described using the principle of least action.
What is a field in the context of physics?
-In physics, a field is a quantity that depends on space and time, varying from place to place and moment to moment. It can be thought of as a measurable quantity, such as the electric field, which influences the behavior of charged particles.
How does the principle of least action relate to the motion of particles?
-The principle of least action states that the path taken by a particle between two points in space-time makes the action stationary (it could be a maximum or minimum). This principle is used to derive the equations of motion for particles, such as Newton's laws of motion, by minimizing the action integral over all possible paths.
What is the difference between a scalar field and a vector field?
-A scalar field is a single quantity that varies from point to point in space and time, like temperature. A vector field, on the other hand, has both magnitude and direction at each point, such as wind velocity, which includes both speed and the direction of the wind.
Why is the concept of space-time important in field theory?
-Space-time is crucial in field theory because fields are functions of space-time coordinates. The behavior of fields and the interactions they describe are fundamentally tied to the geometry and topology of space-time, which is typically considered to have one time dimension and multiple space dimensions.
How does the lecturer connect particle mechanics to field theory?
-The lecturer connects particle mechanics to field theory by considering a particle's position as a field that depends only on time in a space-time with zero spatial dimensions. This analogy extends to more dimensions and allows for the application of the principle of least action to field theory.
What is the role of the Lagrangian in field theory?
-The Lagrangian in field theory is a function that depends on the field and its derivatives with respect to space and time. It is used to express the action principle, which is integral to deriving the equations of motion for the field. The Lagrangian density is integrated over space-time to find the action.
What are the Euler-Lagrange equations?
-The Euler-Lagrange equations are a set of differential equations that arise from the principle of least action. They are used to determine the equations of motion for a field by taking the functional derivative of the action with respect to the field and setting it to zero.
How does the presence of a scalar field affect the motion of a particle?
-The presence of a scalar field can affect the motion of a particle by altering its effective mass. If the scalar field tends to a non-zero stable value, the particle's motion can be described as if it had a mass that is the original mass minus the scalar field value.
What is the significance of the Higgs field in particle physics?
-The Higgs field is a scalar field that is responsible for giving particles mass. It is a fundamental concept in the Standard Model of particle physics, where it explains how particles acquire mass through interaction with the Higgs field.
How does the lecturer illustrate the interaction between a particle and a scalar field?
-The lecturer illustrates the interaction by modifying the Lagrangian for a particle to include a term that is a function of the scalar field. This modification allows the particle to be affected by the field, and the resulting equations of motion describe how the particle moves in the presence of the field.
Outlines
📚 Introduction to Classical Field Theory
The speaker begins by transitioning from particle physics to classical field theory, emphasizing the study of fields rather than particles. Fields are observable quantities that vary with space and time, such as the electric field. The lecture introduces the concept of space-time with one time dimension and multiple space dimensions, which is foundational to field theory. Scalar and vector fields are discussed, with examples including temperature and wind velocity, to illustrate the difference between these types of fields.
🌟 Particle Motion and the Principle of Least Action
The discussion shifts to the motion of particles in nonrelativistic physics, using the principle of least action. The action is defined as an integral of the Lagrangian, which is the difference between kinetic and potential energy. The Euler-Lagrange equations are introduced to describe the motion of particles, which are derived from the principle of least action. The speaker also connects the principle of least action to finding the trajectory of least action between two points in space-time.
🧵 Generalizing Field Theory to Space-Time
The lecturer generalizes the concept of field theory to include space-time dimensions beyond a single time dimension. By considering fields as functions of time and space, the speaker explores the idea of fields in various space-time configurations, from zero-dimensional space to higher dimensions. The potential energy is also discussed in the context of fields, highlighting that it can depend on the field's value, even in a space-time with no spatial dimensions.
🔄 The Action Principle in Field Theory
The action principle is extended to field theory, where the action is considered as a sum over space-time cells. The field's history is represented as a surface in space-time, and the action principle is used to find the field configuration that minimizes the action. The speaker emphasizes that the action principle is a powerful tool that encodes numerous laws of physics and is applicable to field theory in the same way it is to particle mechanics.
📏 The Lagrangian and Field Theory
The lecture delves into the specifics of the Lagrangian in field theory, which is an integral over space and time. The Lagrangian density is introduced as a function of the field and its derivatives with respect to time and space. The speaker outlines the process of constructing a Lagrangian for field theory by considering all possible scalars that can be made from the field and its derivatives, ensuring that the Lagrangian is a scalar and invariant under Lorentz transformations.
🤔 The Euler-Lagrange Equations in Field Theory
The speaker derives the Euler-Lagrange equations for field theory, which are analogous to those in particle mechanics but include a sum over terms for each direction of space-time. The equations are presented in a form that accounts for both time and space derivatives of the field. The lecturer also touches on the implications of including a potential energy term in the Lagrangian, leading to a wave-like motion described by the equations of motion.
🌐 Lorentz Invariance in Field Theory
The importance of Lorentz invariance in field theory is emphasized, with the speaker explaining how to construct invariant quantities and the transformation properties of fields. Scalar fields and four-vectors are discussed, along with their transformation under Lorentz transformations. The lecture also covers how to form scalars from four-vectors and the concept of differentiating a scalar to obtain a four-vector.
🚀 Constructing a Lorentz-Invariant Lagrangian
The speaker outlines the rules for constructing a Lagrangian that is invariant under Lorentz transformations. It is stated that the Lagrangian must be a scalar, and possible scalars that can be included are functions of the field and its derivatives. The lecture also explores the possibility of including higher powers of derivatives and the implications of such inclusions for the complexity of the Lagrangian.
🤓 Particle Interaction with a Scalar Field
The lecture concludes with a discussion on how a particle might interact with a scalar field. A Lagrangian for a particle moving in a pre-established field is proposed, and it is shown that the particle's motion can be affected by the field. The concept of the Higgs field giving mass to particles is touched upon, and the lecturer suggests that the Higgs mechanism is closely connected to the idea of a scalar field affecting particle mass.
🧠 Equations of Motion for a Particle in a Field
The speaker works through the equations of motion for a particle interacting with a scalar field, using the Euler-Lagrange equations. The process is complex, and the resulting differential equation is not simplified. However, the lecturer suggests that if the field tends to a stable non-zero value, the particle's motion can be described as if it had an effective mass that includes the contribution from the field. The Higgs field is mentioned as a real-world example of such a mechanism.
Mindmap
Keywords
💡Classical Field Theory
💡Space-Time
💡Lagrangian
💡Euler-Lagrange Equations
💡Scalar Field
💡Action Principle
💡Potential Energy
💡Quantum Mechanics
💡Higgs Field
💡Lorentz Invariance
💡Wave Equation
Highlights
Introduction to classical field theory as opposed to quantum field theory, emphasizing a foundational understanding of fields.
Explanation of space-time as having one time coordinate and multiple space coordinates, relevant to physical world concepts.
Discussion on the uniqueness of time dimensions in physical theories and the logical challenges of more than one time dimension.
Definition and examples of fields, such as the electric field, temperature, and wind velocity, as observable quantities varying with space and time.
Differentiation between scalar and vector fields, with examples to illustrate the concepts.
Connection between the principles of least action and the Euler-Lagrange equations in classical mechanics.
Transition from particle mechanics to field theory by considering a field as a function of time in a zero-dimensional space.
Generalization of field theory to include a time direction and multiple space coordinates, leading to a field as a function of space and time.
Introduction of the action principle in field theory, suggesting that the physical world is described by an action principle.
Description of the Lagrangian density as a function of fields and their derivatives, which is integral to formulating field theory.
Derivation of the Euler-Lagrange equations for field theory, which are essential for finding the history of a field in space and time.
Construction of a Lagrangian for a particle moving in a pre-established field, illustrating how particles interact with fields.
Potential energy's role in field theory and its relation to the change in energy as the field variable changes.
The concept of a static solution in field theory and its relation to time-independent fields, such as electric or magnetic fields.
Exploration of the wave equation derived from the Lagrangian, which describes wave-like motions in the context of field theory.
Incorporation of special relativity into field theory by ensuring the Lagrangian is a scalar and invariant under Lorentz transformations.
Discussion on the transformation properties of scalar and vector fields under Lorentz transformations.
Construction of invariant quantities and the importance of differentiating scalars with respect to space and time components to form four-vectors.
The Higgs field as a real-world example of a scalar field that can interact with particles and potentially affect their mass.
Challenges in transitioning from classical to quantum mechanics, where most classical field theories do not hold up without inconsistencies.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: