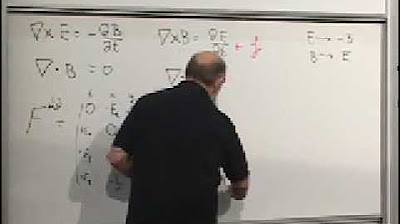Lecture 7 | Quantum Entanglements, Part 3 (Stanford)
TLDRThe video script provided is an in-depth exploration of the dynamics of charged particles in electric and magnetic fields, with a particular focus on how these dynamics are influenced by the principles of relativity. The lecturer begins by discussing the Lorentz force law, which determines the influence of electric and magnetic fields on charged particles, and questions its consistency with relativity. They delve into the need to modify non-relativistic laws of motion to make them invariant across all reference frames. The concept of force is revisited, highlighting the different types of forces in nature and their extensions from non-relativistic to relativistic physics. The script also touches on the similarities between the laws of motion for gravitation and electric forces, and the challenges in extending these laws to the special theory of relativity. The lecturer then introduces the Lorentz force law in the context of special relativity, emphasizing the role of the electric charge, electric field, and magnetic field in influencing the motion of charged particles. The homework assigned involves incorporating the speed of light into the equations through dimensional analysis. The script concludes with a discussion on the transformation properties of electric and magnetic fields under different reference frames, leading to the concept of an anti-symmetric tensor that can describe the electromagnetic field in four dimensions. This tensor, denoted as F mu nu, is central to formulating the equations of motion for charged particles that remain consistent across all reference frames.
Takeaways
- 📚 The program discusses the behavior of charged particles in electric and magnetic fields, emphasizing the role of relativity in influencing these dynamics.
- 🚀 The Lorentz force law, which determines how electric and magnetic fields affect charged particles, must be consistent with the principles of relativity to ensure the laws are the same in every reference frame.
- 🤔 Newtonian mechanics, which works well in classical scenarios, requires modification to account for relativistic effects, particularly when dealing with charged particles moving at significant fractions of the speed of light.
- 🧲 Magnetic effects are inherently relativistic; if the speed of light were infinite, there would be no magnetic force on charged particles, and only electric forces would be present.
- 📐 The laws of motion for charged particles need to be adjusted to account for relativistic effects, which changes the understanding of force from a simple product of mass and acceleration (F=ma) to a more complex concept.
- 🌌 The special theory of relativity generalizes the laws of physics, including those governing the motion of gravitation and electricity, but the generalization for electricity is not a straightforward extension of Newton's laws.
- 🔗 The concept of force is explored in depth, with a distinction made between different types of forces in nature and their extensions from non-relativistic to relativistic physics.
- 🤓 The mass of an object, as defined in relativity, does not change with time, which is a fundamental principle that remains consistent even when considering relativistic effects.
- 🧵 The cross product, a mathematical operation that describes the interaction between two vectors, is used to describe the magnetic force on a charged particle moving in a magnetic field.
- 🏎️ The magnitude of velocity (speed) of a particle in a magnetic field remains constant, provided the magnetic field is static and there are no electric fields present.
- 🔄 The electric and magnetic fields are shown to transform into each other under certain conditions, such as when observed from different reference frames moving relative to each other.
Q & A
What is the Lorentz force law and why is it significant in the context of relativity?
-The Lorentz force law describes the force experienced by a charged particle moving through electric and magnetic fields. It is significant in the context of relativity because it must be consistent with the principles of relativity, ensuring that the laws of physics hold the same for all observers in different reference frames.
How does the concept of force need to be understood in the context of relativistic physics?
-In relativistic physics, the concept of force is not just about where forces come from but involves a deeper understanding of its nature. This is because the principles of relativity require modifications to the Newtonian laws of motion to maintain consistency across different reference frames.
Why does the presence of a magnetic field in one reference frame imply the presence of an electric field in another moving frame?
-The presence of a magnetic field in one reference frame implies the presence of an electric field in another moving frame due to the relativistic transformation properties of these fields. If an observer is moving relative to a magnetic field, they will measure an electric field as well, because the laws of physics, and thus the forces experienced by a charge, must be the same in all reference frames.
What is the role of the speed of light in determining the existence of magnetic forces?
-The speed of light plays a crucial role in determining the existence of magnetic forces. If the speed of light were infinite, there would be no magnetic force on charged particles because the force on charged particles is proportional to their velocity over the speed of light squared. Since magnetic effects are relativistic effects, the finite value of the speed of light allows for magnetic forces when particles move at speeds that are a significant fraction of the speed of light.
How does the concept of momentum transform in special relativity?
-In special relativity, momentum is not simply mass times velocity as in Newtonian physics. Instead, it is mass times the proper velocity, which takes into account the effects of relativity, such as time dilation and length contraction. The momentum is a four-vector, meaning it has components that transform under Lorentz transformations to maintain the same physical laws in all reference frames.
What is the significance of the anti-symmetric tensor in the context of electromagnetic fields?
-The anti-symmetric tensor is significant because it provides a framework to combine the electric and magnetic fields into a single four-dimensional object known as the electromagnetic field tensor (F mu nu). This tensor has six independent components and transforms in a way that preserves the laws of physics across different reference frames, which is essential for the special theory of relativity.
How does the magnitude of velocity of a charged particle change when it is only under the influence of a magnetic field?
-The magnitude of the velocity of a charged particle does not change when it is only under the influence of a magnetic field. This is because the magnetic force acting on the particle is always perpendicular to the particle's velocity, resulting in no work done on the particle and thus no change in its speed.
What is the relationship between the electric and magnetic fields in the electromagnetic field tensor?
-In the electromagnetic field tensor, the electric field components are placed in the time-like components (specifically, the first three components), while the magnetic field components are placed in the space-like components (also the next three components). The tensor is anti-symmetric, which means that it has specific transformation properties that allow the electric and magnetic fields to mix under changes in reference frames.
What is the physical interpretation of the statement F mu nu times u mu equals zero?
-The statement F mu nu times u mu equals zero is a four-dimensional generalization of the fact that the force due to a magnetic field is perpendicular to the velocity of the particle. It implies that in the context of special relativity, the force experienced by a particle (as described by the electromagnetic field tensor) is orthogonal to its four-velocity, ensuring that the particle's path through space-time is consistent across all reference frames.
How do the electric and magnetic fields transform under a Lorentz transformation along the x-axis?
-Under a Lorentz transformation along the x-axis, the component of the electric field along the x-axis (E_x) remains unchanged because it is invariant. However, the components of the electric field perpendicular to the x-axis (E_y and E_z) can transform to include components of the magnetic field, indicating that the electric and magnetic fields mix under such transformations.
What is a scalar wave equation and why is it invariant under Lorentz transformations?
-A scalar wave equation is a second-order partial differential equation that involves the second derivatives of a scalar field with respect to space and time coordinates. It is invariant under Lorentz transformations because it can be written in a form where a scalar quantity (which is the same in all reference frames) is set equal to zero. This invariance is crucial for the physical laws described by the wave equation to hold true in all inertial frames.
Outlines
📚 Introduction to Charged Particles and Relativity
This paragraph introduces the topic of charged particles moving in electric and magnetic fields. It discusses the impact of relativity on these particles and fields, the Lorentz force law, and the need to reconcile it with the principles of relativity. The paragraph also touches on the concept of force in different contexts, from non-relativistic to relativistic physics, and hints at the differences between the laws of gravitation and electrical forces under the special theory of relativity.
🚀 Momentum and the Lorentz Force Law
The second paragraph delves into the definitions of momentum and force within the framework of Newtonian and relativistic physics. It explains the time rate of change of momentum equals force, and how this definition extends to special relativity. The paragraph also introduces the Lorentz force law, which incorporates electric and magnetic forces on a charged object, and challenges the audience to reintroduce the speed of light into the equations for a nonrelativistic limit.
🔗 The Cross Product and Anti-symmetric Tensor
This section explores the cross product of vectors and how it can be represented as an anti-symmetric tensor. It discusses the properties of tensors, their transformation under rotations, and the relationship between the cross product of two vectors and the components of an anti-symmetric tensor. The paragraph establishes the groundwork for understanding how the magnetic field can be represented in terms of tensors, which is crucial for generalizing to other dimensions.
🧲 Magnetic Field as a Vector and Tensor
The fourth paragraph continues the discussion on the magnetic field, emphasizing its dual representation as both a vector and an anti-symmetric tensor. It corrects a previous statement about the components of the cross product and their correspondence to the tensor components. The paragraph also highlights the unique aspects of three-dimensional space that allow for this dual representation and introduces the concept of the magnetic field's geometry in relation to an anti-symmetric tensor.
🤔 The Geometry of Anti-symmetric Tensors
This paragraph examines the geometrical interpretation of anti-symmetric tensors, particularly in the context of the magnetic field. It discusses how each component of the tensor is associated with two axes and the implications of describing a vector by the plane it's perpendicular to. The paragraph also touches on the transformation properties of the tensor under rotations and the distinction between describing a vector by its components versus the planes perpendicular to those components.
🏗️ Components of V cross B and Magnetic Field Effects
The fifth paragraph works through the components of the cross product V cross B, focusing on the third component. It demonstrates how to express this component using the identification of the magnetic field as a tensor. The paragraph also discusses the theorem that the force on a charged particle in a magnetic field is given by V cross B and the implications of this for the particle's motion, including the constancy of speed in a static magnetic field.
📐 Differentiating Velocity in a Magnetic Field
This section focuses on the differentiation of the square of the velocity with respect to time in a magnetic field. It establishes that the magnitude of the velocity (or speed) of a particle does not change when it is solely under the influence of a static magnetic field. The paragraph uses the Lorentz force law to demonstrate this property and highlights the difference between a time-dependent and time-independent magnetic field's impact on the particle's velocity.
🧵 Electric and Magnetic Fields in Different Reference Frames
The seventh paragraph discusses how electric and magnetic fields transform under different reference frames moving with relative velocity. It explains that a pure magnetic field in one frame can appear as a combination of electric and magnetic fields in another frame. The paragraph also touches on the concept of four-vectors and the need to work with four-dimensional space-time to accurately describe the transformation properties of these fields.
🔋 The Electromagnetic Field Tensor
This paragraph introduces the electromagnetic field tensor, an anti-symmetric tensor that combines the electric and magnetic fields. It discusses the structure of this tensor and how it fills the six components of the electromagnetic field. The paragraph also explores the historical context of the tensor's development and its role in the force experienced by charged particles within the framework of special relativity.
🌐 Four-Velocity and Four-Momentum
The ninth paragraph defines the four-velocity and four-momentum in the context of special relativity. It explains how the components of these four-vectors are derived from the particle's ordinary velocity and mass. The paragraph also establishes the relationship between the force experienced by a particle and the anti-symmetric tensor, leading to the conclusion that the force must be orthogonal to the four-velocity.
🔗 Deriving the Lorentz Force Law
The tenth paragraph works through the derivation of the Lorentz force law using the four-vector notation. It shows how the force experienced by a charged particle is related to the electric and magnetic fields and the particle's velocity. The paragraph also discusses the transformation properties of the electromagnetic field tensor and how these properties ensure that the equations of motion for a charged particle remain consistent across different reference frames.
🌌 Wave Equations and Scalar Waves
The final paragraph shifts the focus to wave equations and scalar waves. It introduces the concept of a scalar field and its differentiation to form covariant components of a four-vector. The paragraph also discusses the transformation properties of these derivatives and sets the stage for a future discussion on Maxwell's equations and their Lorentz invariance.
📉 Invariance of Wave Equations
This paragraph discusses the importance of the invariance of wave equations under Lorentz transformations. It presents a simple wave equation and explains that for an equation to be invariant, it must result in a scalar, which remains the same across all reference frames. The paragraph concludes with a note on the upcoming discussion on Maxwell's equations in a covariant form, which will be explicitly Lorentz invariant.
Mindmap
Keywords
💡Relativity
💡Lorentz Force Law
💡Charged Particles
💡Electric Field
💡Magnetic Field
💡Cross Product
💡Four-Vector
💡Antisymmetric Tensor
💡Covariant and Contravariant Vectors
💡Wave Equation
💡Maxwell's Equations
Highlights
Discussion on charged particles moving in electric and magnetic fields and the impact of relativity on these motions.
Exploration of the Lorentz force law and its consistency with the principles of relativity across different reference frames.
Explanation of the need to modify non-relativistic laws of motion to maintain consistency in all reference frames.
Insight into the concept of force in nature, and how it extends from non-relativistic to relativistic physics.
Clarification that magnetic effects are relativistic effects and would not exist if the speed of light were infinite.
Comparison of the laws of motion for gravitation and electricity, noting their similarities and the need for a generalization for special relativity.
Introduction to the basic laws of electrical and magnetic forces on charged particles and their equations of motion.
Differentiation between the concepts of momentum and velocity in the context of special relativity.
Assignment of homework to incorporate the speed of light into the equations through dimensional analysis.
Derivation of the Lorentz force law components and their relation to electric charge, electric field, and magnetic field.
Discussion on the cross product as a tensor and its significance in describing the interaction between charged particles and fields.
Proof that the speed of a particle does not change when it is only influenced by a magnetic field.
Explanation of how electric and magnetic fields mix under velocity transformations, leading to the need for four-vector notation.
Introduction of the electromagnetic field tensor F mu nu, which combines electric and magnetic fields into a four-dimensional anti-symmetric tensor.
Derivation of the force law for charged particles in the context of special relativity, leading to a four-vector equation.
Theorem proving that the force four-vector F mu is orthogonal to the four-velocity u mu, generalizing the concept from the Lorentz force law.
Demonstration of how the Lorentz force law can be derived from the four-vector equation by considering slow velocities.
Discussion on the transformation properties of the electromagnetic field tensor under Lorentz transformations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: