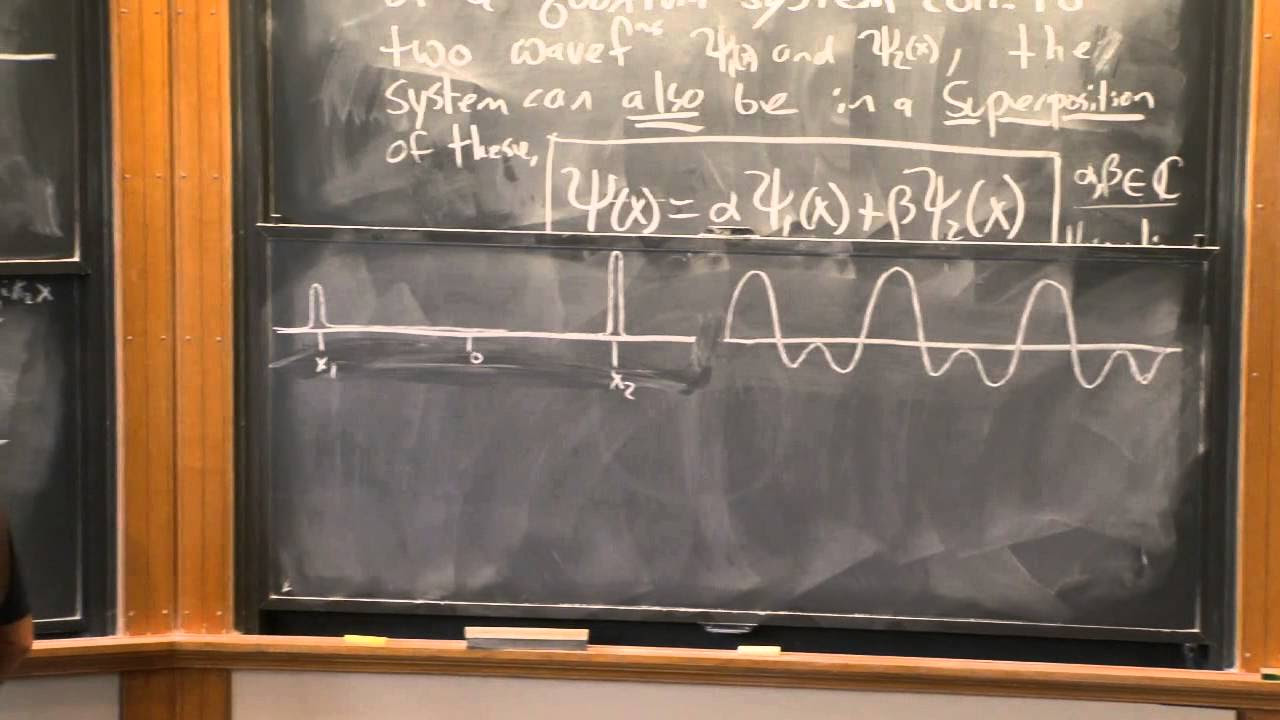Lecture 10 | The Theoretical Minimum
TLDRThe video script, presumably from a lecture at Stanford University, delves into the foundational aspects of quantum mechanics, with a focus on the Schrödinger equation and the Heisenberg Uncertainty Principle. The lecturer explains the concept of negative energy and its implications for a stable world, emphasizing that a stable world requires all particles to have positive energy relative to the vacuum. The idea of Fermions and Bosons is introduced, highlighting their distinct properties and the implications for quantum field theory. The Heisenberg Uncertainty Principle is derived using the triangle inequality, demonstrating the inherent limits of precision in measuring complementary variables like position and momentum. The script also explores the relationship between the wave function and classical mechanics, showing how expectation values of observables like position and momentum relate to classical concepts of velocity and force. The conditions under which quantum mechanics can approximate classical mechanics are discussed, pointing to the importance of particle mass and the smoothness of potential energy functions. The lecture concludes with a discussion on the applicability of quantum mechanics to macroscopic objects and the transition to classical behavior in certain conditions.
Takeaways
- 📚 The concept of negative energy in quantum mechanics is theoretically possible but unstable in the real world, as it would lead to a vacuum state that is not the lowest energy state.
- 🚫 Negative energy particles, if they existed, could destabilize the world by lowering the energy of empty space, leading to the creation of more particles.
- 🌟 The stability of the world requires all particles to have positive energy relative to the vacuum, which is considered the state of lowest energy.
- 🚀 Dr. Dra understood the concept of Fermions, particles that cannot be in the same state simultaneously, which is derived from relativistic Quantum field Theory and is akin to the Pauli Exclusion Principle.
- 🤔 The vacuum, when considered as a state filled with all negative energy particles, can only be achieved with Fermions, as Bosons would destabilize the vacuum due to their ability to occupy the same state.
- 🌱 The simplified model of the Dirac equation is a good theory for neutrinos or one-dimensional neutrinos but not for photons, which are Bosons.
- 🧲 The foundation of quantum mechanics was covered, but applications and more complex systems like the harmonic oscillator were not, indicating a need for further study in subsequent quarters.
- ⚛️ The wave function, represented by Ψ, is a measure of the probability amplitude that a particle is located at a particular position.
- 🔄 The position and momentum wave functions are related through a Fourier transform, highlighting the dual nature of quantum particles.
- 📊 The Heisenberg Uncertainty Principle states that the more precisely the position of a particle is known, the less precisely its momentum can be known, and vice versa.
- 🤓 The Schrodinger equation governs how the wave function changes with time and is fundamental to understanding quantum mechanical systems.
Q & A
What is the significance of negative energy in quantum mechanics?
-Negative energy is significant because if particles with negative energy existed, they could lower the energy of a system indefinitely, leading to an unstable world. In a stable world, all particles must have positive energy relative to the vacuum, which is considered the state of lowest energy.
What is the role of the Hamiltonian in quantum mechanics?
-The Hamiltonian represents the total energy of the system and is used to describe how the quantum state of a system changes over time. It is crucial in the Schrödinger equation, which determines the evolution of the wave function.
How does the Pauli Exclusion Principle relate to Fermions and Bosons?
-The Pauli Exclusion Principle states that no two fermions can occupy the same quantum state simultaneously. Fermions are particles that obey this principle, while bosons do not. Bosons can occupy the same state, which has implications for how they interact and behave in quantum systems.
What is the uncertainty principle in quantum mechanics?
-The uncertainty principle states that it is impossible to simultaneously know the exact position and momentum of a particle. The more precisely one property is measured, the less precisely the other can be known. This principle arises from the non-commutativity of the position and momentum operators.
How is the wave function related to the position and momentum of a particle?
-The wave function is a mathematical description of the quantum state of a particle. It provides the probability distribution for the position and momentum of the particle. The wave function in position space represents the probability amplitude for finding the particle at various locations, while the momentum space wave function gives the probability distribution for the particle's momentum.
What is the role of the Schrödinger equation in quantum mechanics?
-The Schrödinger equation describes how the wave function of a quantum system changes over time. It is a fundamental equation in quantum mechanics that allows for the calculation of the dynamics of quantum systems and the determination of the probability distribution of physical quantities.
What is the relationship between the wave function and the probability distribution of a particle?
-The wave function provides the probability distribution for the position and momentum of a particle. The square of the wave function's absolute value gives the probability density of finding the particle at a particular position or with a particular momentum.
Why is it said that the vacuum is unstable if it contains particles of negative energy?
-The vacuum would be unstable if it contained particles of negative energy because the energy of the system could be lowered indefinitely by adding more negative energy particles. This would contradict the principle that the vacuum, or empty space, should be the state of lowest possible energy.
How does the concept of Fermions and Bosons affect the behavior of particles in a quantum system?
-Fermions, which obey the Pauli Exclusion Principle, cannot occupy the same quantum state as another fermion, leading to phenomena like electron filling in atomic orbitals. Bosons, on the other hand, can occupy the same state, which allows for phenomena such as the laser, where numerous photons occupy the same quantum state.
What is the significance of the Heisenberg Uncertainty Principle in the context of the wave function?
-The Heisenberg Uncertainty Principle implies that the wave function cannot be sharply localized in both position and momentum space simultaneously. This means that the more precisely the position of a particle is known, the less precisely its momentum can be known, and vice versa.
How does the expectation value of a quantum mechanical system relate to classical mechanics?
-In quantum mechanics, the expectation value of an observable like position or momentum represents the average or typical value that could be measured in an experiment. For a particle described by a wave function that is well-localized and does not spread out significantly over time, the expectation values calculated from the wave function will follow the classical equations of motion, thus bridging the gap between quantum and classical mechanics.
Outlines
🌟 Negative Energy and Stability in Quantum Mechanics
This paragraph discusses the concept of negative energy in quantum mechanics. It explains that a model with both positive and negative energy is unstable because negative energy particles could lower the overall energy of the system, leading to an unstable world. The speaker emphasizes that a stable world requires all particles to have positive energy relative to the vacuum, which is considered the state of lowest energy.
🚀 Fermions and Bosons in Quantum Field Theory
The speaker introduces fermions and bosons, particles that obey the Pauli Exclusion Principle and those that don't, respectively. Fermions cannot occupy the same state simultaneously, while bosons can. The paragraph explores the idea that the vacuum, a state of lowest energy, could be filled with negative energy particles, but only if they are fermions. This is because fermions cannot be in the same state, thus preventing an infinite lowering of energy.
🌌 Quantum Mechanics Foundations and Applications
The paragraph touches on the basics of quantum mechanics covered in the course and acknowledges the lack of coverage on certain topics like the harmonic oscillator. It also mentions the excitement generated by the concept of quantum entanglement and the discussions it spurred online. The speaker promises to revisit quantum mechanics after covering relativity and field theory to delve deeper into its foundational structures.
📐 The Wave Function and the Schrödinger Equation
The focus here is on the wave function, its relation to position and momentum, and the Schrödinger equation. The speaker explains that the wave function represents the amplitude of a particle being in a particular position and how it can be transformed into momentum space. The paragraph also introduces the concept that the position and momentum of a particle cannot be simultaneously measured with arbitrary precision, a principle known as the Heisenberg Uncertainty Principle.
🔍 Uncertainty Principle and Its Implications
This paragraph delves into the mathematical derivation of the uncertainty principle. The speaker demonstrates how the uncertainty in position (ΔX) and the uncertainty in momentum (ΔP) are related, showing that the product of these uncertainties is greater than or equal to a constant. The principle is derived using the properties of Fourier transforms and the commutation relations between position and momentum operators.
🤔 The Physical Interpretation of the Uncertainty Principle
The speaker explores the physical meaning behind the uncertainty principle, addressing common misconceptions and providing clarifications. It is emphasized that the principle does not mean that it's impossible to simultaneously know the position and momentum of a particle, but rather that the more precisely one property is known, the less precisely the other can be known. The paragraph also touches on the relationship between the uncertainty principle and the behavior of wave functions.
🧲 Potential Energy and the Schrödinger Equation
In this paragraph, the speaker discusses how to incorporate potential energy into the Schrödinger equation. The Hamiltonian for a quantum mechanical particle is introduced, which includes the kinetic energy term (p^2 / 2m) and a potential energy term (V(x)). The paragraph explains that the action of the potential energy operator on a wave function is to multiply it by the potential energy function V(x).
🚦 Expectation Values and the Time Evolution of Wave Packets
The focus shifts to how expectation values, particularly of position and momentum, change with time according to the Schrödinger equation. The speaker shows that the velocity of the center of a wave packet is given by the expectation value of the momentum divided by the mass (p/M). The paragraph also aims to connect the quantum mechanical description of wave packets with their classical counterparts, emphasizing the conditions under which the correspondence principle holds.
🔄 Classical Mechanics and Quantum Mechanics Correspondence
This paragraph discusses the conditions under which quantum mechanics reproduces the behavior of classical mechanics. It is noted that classical behavior is expected when dealing with heavy particles and smooth potentials, where the wave function remains coherent and well-localized. In contrast, light particles or particles encountering sharp potential features can exhibit more pronounced quantum behavior, leading to deviations from classical predictions.
🏠 Closing Remarks and Acknowledgments
The speaker concludes the discussion with a mention of the interplay between the mass of particles and the smoothness of potentials in determining whether classical or quantum mechanical descriptions are more appropriate. They also express a personal note of stepping away to attend to a family matter, adding a touch of personal context to the academic discourse.
Mindmap
Keywords
💡Hamiltonian
💡Wave Function
💡Negative Energy
💡Vacuum State
💡Fermions
💡Bosons
💡Energy Conservation
💡Uncertainty Principle
💡Schrödinger Equation
💡Momentum Space
💡Quantum Harmonic Oscillator
Highlights
Discussion on the concept of negative energy in quantum mechanics and its implications for the stability of the world.
Explanation of Fermi and Bose particles, including the Pauli Exclusion Principle and their role in quantum field theory.
Insight into the idea that a stable world requires all particles to have positive energy relative to the vacuum.
Introduction to the Schrödinger equation and its connection to wave functions and particle position.
Derivation and explanation of the Heisenberg Uncertainty Principle using the triangle inequality.
Discussion on the conditions under which quantum mechanics can reproduce classical mechanics, focusing on the mass of particles and smoothness of potentials.
The impact of potential energy functions on wave packet dynamics and how they relate to classical orbits.
Integration by parts technique used to derive quantum mechanical relationships and their classical analogs.
The role of the Hamiltonian operator in governing the time evolution of quantum states.
Explanation of how the expectation value of momentum is related to the velocity of a wave packet.
Demonstration of how the Schrödinger equation can predict the classical motion of a particle under certain conditions.
The importance of the wave function's coherence and localization for it to exhibit classical-like behavior.
Conditions for a quantum system to exhibit classical behavior: heavy particles and smooth potentials.
The contrast between quantum and classical behavior in the context of particle mass and potential features.
Historical context provided by the Rutherford scattering experiment and its implications for atomic structure.
Practical examples illustrating the scattering of particles and waves when encountering structures smaller than their wavelength.
The significance of the uncertainty principle in understanding the limitations of classical physics and the transition to quantum mechanics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: