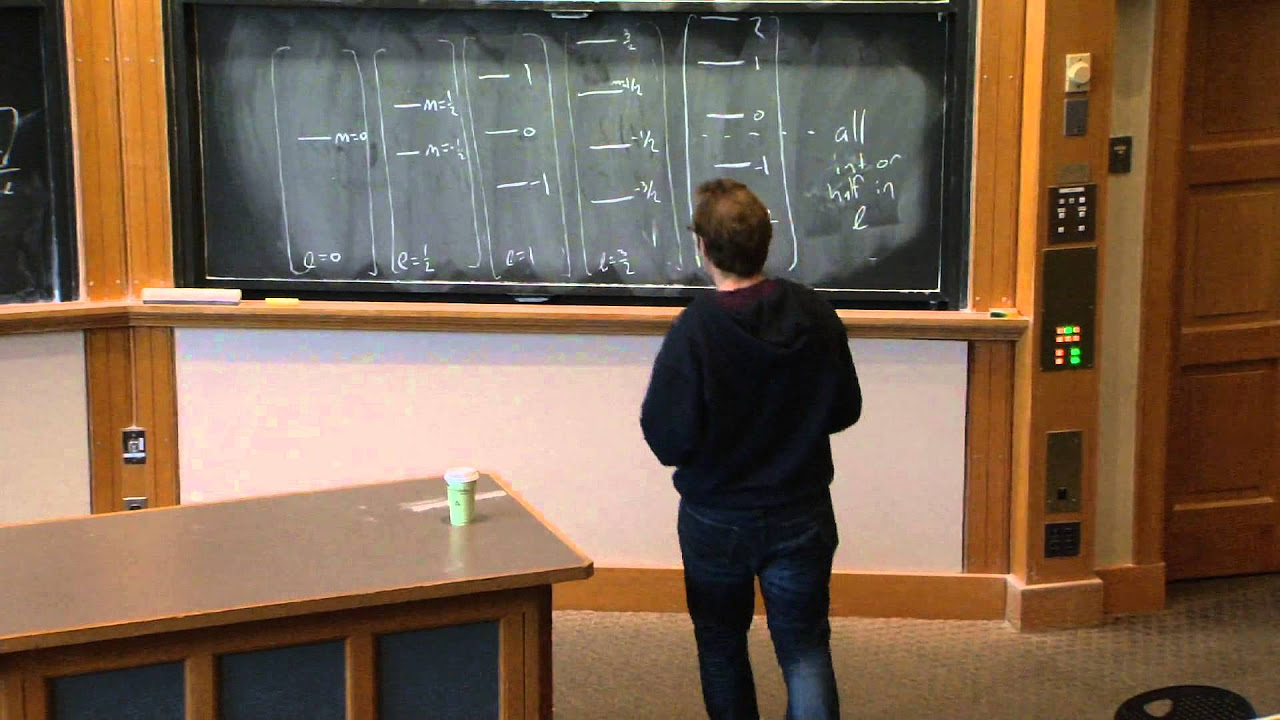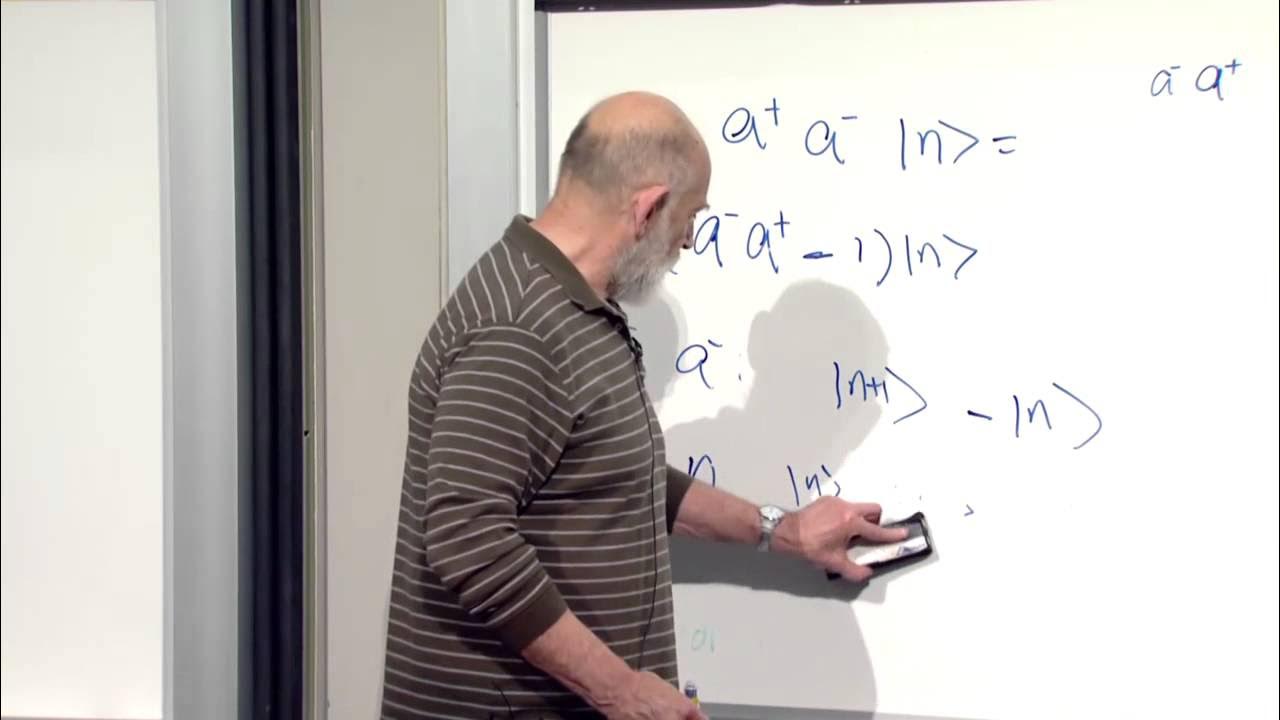Advanced Quantum Mechanics Lecture 3
TLDRThe video script is an in-depth lecture on quantum mechanics, specifically focusing on the angular momentum operators and the harmonic oscillator. It begins with a discussion on angular momentum in quantum systems, explaining the conservation of angular momentum and its relation to the orbital plane in a central force field. The lecturer delves into the algebra of angular momentum operators, illustrating how they form multiplets with specific numbers of states. The concept of wave functions and their angular dependence is also explored, with the讲师 (lecturer) using two-dimensional angular momentum as an example to explain the eigenstates and the role of the radial dependence. The lecture then transitions into the central force problem, using classical physics intuition to make educated guesses about the quantum mechanical solutions. It highlights the significance of the centrifugal force in preventing particles from reaching the origin when angular momentum is present. The讲师 (lecturer) also introduces the concept of spherical harmonics, which are solutions to the angular part of the wave function in three dimensions. Moving on to the harmonic oscillator, the script discusses its classical and quantum mechanical descriptions. The讲师 (lecturer) presents the Hamiltonian for a one-dimensional harmonic oscillator and uses it to derive the energy levels and eigenstates. The raising and lowering operators, or ladder operators, are introduced as tools to move between these energy levels. The script concludes with a discussion on the zero-point energy, a quantum mechanical phenomenon where even the ground state of a harmonic oscillator possesses a finite amount of energy due to the Heisenberg uncertainty principle. Throughout the script, the lecturer emphasizes the importance of understanding the algebraic properties of operators and the physical implications of quantum mechanics on systems such as atoms and harmonic oscillators. The lecture is rich with mathematical derivations and provides a solid foundation for further exploration into quantum mechanics.
Takeaways
- 📚 Angular momentum is a conserved quantity in quantum mechanics, and it is related to the rotational symmetry of a system.
- 🚀 The angular momentum operator affects the angular dependence of a particle's wave function, not the radial component.
- 🌀 In a central force field, the angular momentum vector is perpendicular to the orbital plane, and its conservation implies the orbital plane remains constant.
- 🔍 Eigenstates of the angular momentum operator can be found by solving differential equations that relate to the angular part of the wave function.
- ⚙️ The algebra of angular momentum operators, such as commutation relations, is crucial for understanding the structure of multiplets and the quantum numbers associated with angular momentum states.
- 🌟 The magnitude of the angular momentum squared (L²) is a key quantity in quantum mechanics, and it differs slightly from the classical expectation due to quantum corrections.
- 📈 The energy levels of states with different angular momentum in a central potential are organized by the number of nodes in the wave function, with more nodes corresponding to higher energy.
- 🧲 The centrifugal force is a significant factor in the motion of particles in a central force field, especially when considering non-zero angular momentum states.
- 📊 The effective potential in a central force problem includes the original potential plus a centrifugal barrier term, which is significant at small radii.
- ⚛️ The Hamiltonian for a central force problem can be simplified to a one-dimensional problem once the angular momentum is known, allowing for the separation of angular and radial parts of the wave function.
- 🤔 The solutions to the Schrödinger equation for a central force problem are called spherical harmonics, which are functions of angles and are crucial for describing the angular part of the quantum state.
Q & A
What is angular momentum in the context of quantum mechanics?
-In quantum mechanics, angular momentum is a property of a particle that describes its rotational motion around a specific axis. It is a vector quantity that is conserved in a system with rotational symmetry. The angular momentum operator is related to the angular dependence of the particle's wave function.
What is the significance of the angular momentum operator in three dimensions?
-In three dimensions, the angular momentum operator is significant because it helps describe the wave function of a particle in a central force field. It involves two quantum numbers, one for the magnitude of the angular momentum (L) and another for its projection along a specific axis (M). The eigenstates of these operators are crucial for solving problems like the hydrogen atom.
What are the commutation relations of the angular momentum operators?
-The commutation relations of the angular momentum operators are given by [Lx, Ly] = iħLz, [Ly, Lz] = iħLx, and [Lz, Lx] = iħLy, where ħ is the reduced Planck constant and Lx, Ly, Lz are the components of the angular momentum vector along the x, y, and z axes, respectively.
How does the raising and lowering operator concept apply to angular momentum?
-The raising (L+) and lowering (L-) operators are used to move between different eigenstates of the angular momentum within a multiplet. The raising operator increases the angular momentum projection quantum number m by one unit, while the lowering operator decreases it by one unit. These operators are essential for constructing the ladder of energy levels in problems like the harmonic oscillator.
What is the role of the Hamiltonian in the central force problem?
-In the central force problem, the Hamiltonian describes the total energy of the system. It includes the kinetic energy associated with the radial motion and the potential energy due to the central force. The Hamiltonian commutes with the angular momentum operator, which leads to the conservation of angular momentum and simplifies the problem to a one-dimensional effective problem in the radial coordinate.
Why is the ground state of a quantum harmonic oscillator non-zero?
-The ground state energy of a quantum harmonic oscillator is non-zero due to the Heisenberg uncertainty principle. It is impossible for both the position and momentum of a particle to be precisely zero at the same time. The ground state corresponds to the lowest possible energy, which is the zero-point energy, a characteristic feature of quantum systems.
What is the energy spectrum of a quantum harmonic oscillator?
-The energy spectrum of a quantum harmonic oscillator is quantized and given by E = (n + 1/2)ħω, where n is a non-negative integer, ħ is the reduced Planck constant, and ω is the angular frequency of the oscillator. This means that the energy levels increase in integer steps starting from the ground state energy of 1/2ħω.
How do the ladder operators (a+ and a-) of the harmonic oscillator relate to the energy levels?
-The ladder operators a+ (raising operator) and a- (lowering operator) are used to move up and down the energy ladder of the harmonic oscillator. Applying a+ to an energy eigenstate increases its energy by ħω, while applying a- decreases it by the same amount. The ground state is defined as the state that cannot be lowered any further by the action of a-.
What is the significance of the commutation relation [a-, a+] = 1 in the context of the harmonic oscillator?
-The commutation relation [a-, a+] = 1 is crucial for the harmonic oscillator because it allows us to establish the ladder structure of the energy levels. It shows that the action of a+ on a state increases its energy eigenvalue by one unit, and similarly, a- decreases it by one unit, thus creating a ladder of energy states.
What is the role of the Hermitian property in the context of the harmonic oscillator's energy levels?
-The Hermitian property of an operator ensures that it has a complete set of eigenvalues and eigenvectors, which are real and orthogonal, respectively. For the harmonic oscillator, the Hamiltonian is Hermitian, which guarantees that it has a complete set of energy eigenstates corresponding to real energy eigenvalues, forming a basis for the quantum states of the system.
How does the Heisenberg uncertainty principle manifest in the quantum harmonic oscillator?
-The Heisenberg uncertainty principle states that the position and momentum of a particle cannot both be precisely known at the same time. In the quantum harmonic oscillator, this principle manifests as the zero-point energy, which ensures that the ground state energy is non-zero, reflecting the inherent uncertainty in the exact values of position and momentum even in the lowest energy state.
Outlines
😀 Angular Momentum and Quantum Mechanics
The paragraph discusses angular momentum in the context of quantum mechanics. It explains how the angular momentum operator works and its relation to the states of multiplets. The speaker uses the example of a particle in a central force field to illustrate the conservation of angular momentum and its vector nature. The wave function's angular dependence is tied to the angular momentum operator, and the concept of angular momentum eigenstates in two dimensions is introduced, leading into a discussion on the three-dimensional case.
🔍 Exploring Angular Momentum in 3D
This section delves deeper into the three-dimensional aspects of angular momentum. It emphasizes that angular momentum is about the angular dependence of wave functions and that the radial part is irrelevant to it. The paragraph introduces specific wave functions, Y of theta and Phi, which are crucial to determining the angular momentum of a state. The commutation relations of angular momentum operators are mentioned, and the use of raising and lowering operators (L+ and L-) to move through the spectrum of eigenvalues of LZ is explained.
🚀 The Spectrum of Angular Momentum
The paragraph explores the spectrum of angular momentum, discussing how it can either consist of integers or half-integers and the implications of this for the structure of angular momentum states. It also explains the concept of the maximum value of M (denoted as L) and how it defines the end of the spectrum. The importance of symmetry in the spectrum about the origin is highlighted, and the consequences of applying L+ and L- operators are discussed.
🌌 Angular Momentum Multiplets and Their Properties
The focus shifts to angular momentum multiplets, which are collections of states characterized by a given value of angular momentum. The paragraph explains that these multiplets have 2L + 1 states and that all states within a multiplet share the same magnitude of the angular momentum. The concept of the magnitude of the angular momentum vector squared (L squared) is introduced, and how it relates to the eigenvalues of a multiplet is discussed.
🤔 Quantum Correction in Angular Momentum
This section discusses a quantum correction to the angular momentum, where the square of the angular momentum (L squared) for the top state in a multiplet is not simply L times L, but L times L plus one. The paragraph also touches on the implications of this correction and how it differs from classical mechanics. The concept that all states in a multiplet share the same L squared value is emphasized.
🧮 Commutator Properties of Angular Momentum
The paragraph introduces an exercise to prove that the square of the angular momentum (L squared) commutes with any of the components of angular momentum. This commutator property is key to understanding the structure of angular momentum eigenstates. The proof involves algebraic manipulation and highlights the importance of the commutator in quantum mechanics.
🌟 Angular Momentum and Central Force Problems
The discussion moves to the central force problem, which is a significant application of angular momentum in quantum mechanics. The paragraph outlines the process of solving the Schrödinger equation for a central force problem using classical physics intuition and quantum mechanical tricks. The importance of the angular momentum being conserved and its relation to the Hamiltonian is highlighted.
📚 Solving the Schrödinger Equation for Atoms
This section focuses on solving the Schrödinger equation for atomic systems. It explains how the solutions to the equation provide the energy levels and wave functions of an atom. The paragraph discusses the concept of effective potential and how it is used to find the energy spectrum of an atom. The solutions are expressed in terms of spherical harmonics, which are functions of angles and are key to the angular part of the wave function.
🔬 Energy Levels and Nodes in Quantum States
The paragraph explains the relationship between the number of nodes in a wave function and its energy level. It states that the number of nodes characterizes the different energy levels, with more nodes corresponding to higher energy. The concept of bound states and their relation to discrete energy levels is introduced, and the idea that angular momentum affects the energy levels is discussed.
🌈 Degeneracy and Spectrum of Atomic States
The discussion concludes with the degeneracy of energy levels in atoms and the overall spectrum. The paragraph explains that for a Coulomb potential, there is a special degeneracy where certain states with different angular momentum have the same energy. This is a special case and is not generally true for other potentials. The paragraph also touches on the impact of factors like the finite size of the nucleus on this degeneracy.
🎓 Solving the Schrödinger Equation in Quantum Mechanics
The final paragraph summarizes the approach to solving the Schrödinger equation in quantum mechanics. It emphasizes the use of angular momentum eigenstates and the transformation to a one-dimensional problem after accounting for the angular parts. The paragraph also mentions the importance of the Hamiltonian in determining the energy levels and eigenvectors of the system.
Mindmap
Keywords
💡Angular Momentum
💡Eigenstates
💡Central Force Field
💡Wave Function
💡Quantum Mechanical Operator
💡Spherical Harmonics
💡Eigenvalues
💡Raising and Lowering Operators
💡Coulomb Potential
💡Schrödinger Equation
💡Hamiltonian
Highlights
Angular momentum is conserved in a central force field, leading to the orbital plane being conserved as well.
The particle in a central force field is described quantum mechanically by a wave function with angular momentum related to the wave function's angular dependence.
In two dimensions, angular momentum is the generator of rotations about the perpendicular axis, and its quantum mechanical operator structure is given by the derivative with respect to the angle.
Angular momentum eigenstates are functions that satisfy a differential equation involving the angular momentum operator, leading to solutions like e^(iLθ), where L is an integer.
The radial dependence in a wave function does not affect its angular momentum, implying that angular momentum is solely about the angular dependence.
In three dimensions, specific wave functions involving Y of theta and Phi determine the angular momentum of a state and are affected by rotating configurations.
The angular momentum operators LZ, LX, and LY have certain commutation relations that are fundamental to their algebraic manipulation.
L+ and L- operators act as raising and lowering operators for the eigenvalues of LZ, allowing for the construction of the spectrum of angular momentum.
The spectrum of angular momenta is either integers or half-integers, with each collection of states ending at some highest point and symmetrically at the lowest point.
A multiplet of states characterized by a given value of angular momentum has 2L + 1 states, where L is the maximum value of M.
The magnitude of the angular momentum is defined as the square of the angular momentum vector, which is an operator in quantum mechanics.
The states in a multiplet have the same value of the magnitude of the angular momentum, with the square of the angular momentum given by L(L + 1).
The angular momentum eigenstates are spherical harmonics, which are functions on a unit sphere analogous to two-dimensional functions.
All states in a multiplet have the same energy due to the angular momentum commuting with the Hamiltonian in a central force problem.
The central force problem can be reduced to a one-dimensional problem by considering the radial direction only, after accounting for the angular momentum.
The effective potential energy for the radial problem includes a centrifugal barrier, which prevents particles with angular momentum from getting to the origin.
The solutions to the time-independent Schrödinger equation for the radial part of the wave function give the energy levels and wave functions of the atom.
The number of nodes in the wave function is related to the energy level, with more nodes corresponding to higher energy.
The energy spectrum of an atom in a central force potential is characterized by multiplets of states with increasing energy and a specific degeneracy pattern for the Coulomb potential.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: