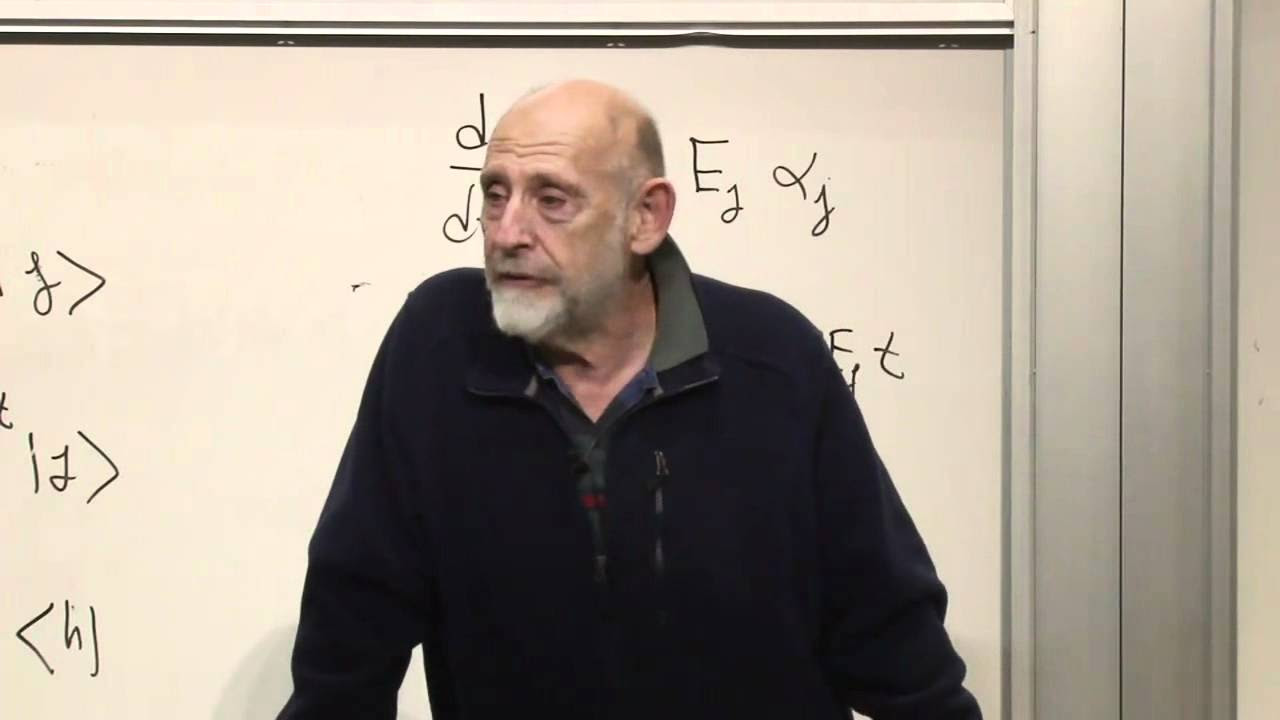Lecture 9 | The Theoretical Minimum
TLDRThe video script is an in-depth exploration of quantum mechanics, focusing on the foundational concepts and mathematical frameworks that underpin the subject. It delves into the principles of quantum entanglement, the superposition of states, and the evolution of quantum systems over time. The lecturer introduces the notion of a Hamiltonian operator, which governs the time evolution of quantum states, and discusses its role in the Schrödinger equation. The script also covers the Heisenberg Uncertainty Principle, illustrating how position and momentum are conjugate variables, and how their uncertainties are inversely related. Fourier analysis is used to connect the position and momentum bases, highlighting the reciprocal relationship between these two fundamental properties of quantum systems. The lecture concludes with a discussion on the behavior of wave functions for particles described by simple Hamiltonians, emphasizing the differences between classical and quantum descriptions of particle motion.
Takeaways
- 🧲 Entanglement is a fundamental subject in quantum mechanics, representing the interconnectedness of quantum states.
- 📚 The foundations of quantum mechanics are based on simple systems, with the understanding that more complex systems can be built upon these principles.
- 📏 In classical mechanics, empirical observations lead to mathematical formulations, whereas in quantum mechanics, the basic empirical observations involve the apparatus that measures quantum states.
- 🌐 The concept of superposition allows for the combination of states, including the number of particles, which is crucial for understanding quantum systems.
- 🎚 Quantum states can be described using wave functions, which are complex mathematical functions that provide probabilities for different outcomes when measuring a quantum system.
- 🚀 The Hamiltonian operator is central to the Schrödinger equation and governs the time evolution of quantum states, analogous to energy in classical mechanics.
- 🛣️ For a free particle (no forces acting upon it), the Hamiltonian is often taken to be the kinetic energy, which is proportional to the square of the momentum.
- 🌈 Fourier analysis and the Dirac Delta function are essential mathematical tools in quantum mechanics, particularly for transforming between position and momentum space representations.
- ⚖️ The Heisenberg Uncertainty Principle implies that certain pairs of physical properties, like position and momentum, cannot both be precisely known at the same time.
- 📐 The inner product of wave functions is used to calculate probabilities in quantum mechanics, which is a key aspect of interpreting the results of quantum measurements.
- 🔄 The time evolution of quantum states is unitary, meaning it preserves the total probability and is described by the Hamiltonian through the Schrödinger equation.
Q & A
What is the central concept of quantum mechanics discussed in the transcript?
-The central concept discussed in the transcript is quantum entanglement, which is described as the heart of quantum mechanics.
What is the simplest empirical observation in quantum mechanics?
-The simplest empirical observation in quantum mechanics is the measurement of a spin in an apparatus that yields outcomes of 1 or 0.
How does the state of a system evolve when starting with a singlet and triplet superposed?
-The singlet remains a singlet and does not emit a photon, but the triplet evolves into a singlet and emits a photon, resulting in an entangled state of the electrons but not with the radiation field.
What is the relationship between the Dirac Delta function and Fourier analysis?
-The Dirac Delta function can be represented as a Fourier transform or a sum of plane waves, which is an important relationship in quantum mechanics.
What is the significance of the plane wave in quantum mechanics?
-A plane wave, represented by e to the IPX, is significant because it has a wave-like character and is used to decompose a wide class of functions in quantum mechanics.
How does the concept of superposition apply to the number of particles in a quantum system?
-Superposition in quantum mechanics allows for the combination of states where there are no particles and states where there is one particle, as any two states can be superposed.
What is the role of the Hamiltonian in quantum mechanics?
-The Hamiltonian in quantum mechanics governs the time evolution of the state vector and is associated with the total energy of the system.
How is the Heisenberg uncertainty principle related to the concept of Fourier transforms?
-The Heisenberg uncertainty principle states that the more precisely one property of a pair (like position and momentum) is known, the less precisely the other can be known. This is related to Fourier transforms as the narrower the range of one property (e.g., momentum), the broader the other (e.g., position) will be.
What is the simplest Hamiltonian for a quantum particle?
-The simplest Hamiltonian for a quantum particle is one that is a constant times the momentum operator, which can describe particles like neutrinos moving at the speed of light.
How does the expectation value of position behave in the context of the simple Hamiltonian where H = C times P?
-In the context of the simple Hamiltonian where H = C times P, the expectation value of position moves with a uniform velocity C, similar to classical mechanics.
What is the difference between the wave function of a particle with definite momentum and the wave function in the momentum basis?
-The wave function of a particle with definite momentum is a function of position that oscillates endlessly and is delocalized. The wave function in the momentum basis, on the other hand, is obtained by taking the Fourier transform of the position space wave function and represents the probability amplitude for finding different momenta.
Outlines
😀 Quantum Mechanics and Entanglement
The paragraph discusses the importance of entanglement in quantum mechanics, noting it as the heart of the subject. It emphasizes the shift from studying the foundations to examining examples within the field. The speaker also touches on the basic empirical observations in quantum mechanics, using the example of an apparatus that measures spin, and discusses the concept of a system involving a singlet and a triplet state with a photon.
🧐 Superposition and Quantum States
This section delves into the concept of superposition in quantum mechanics, illustrating how states of particles, including the number of particles, can be superposed. It explains the transition of a system from an unentangled to an entangled state upon photon emission. The paragraph also explores the mathematical interlude involving Fourier analysis and the Dirac Delta function, which are essential tools for understanding particle motion in quantum mechanics.
📐 Fourier Analysis and Plane Waves
The paragraph focuses on Fourier analysis, explaining how a wide class of functions can be expressed as sums or integrals of plane waves. It details the process of decomposing a function into plane waves and introduces the concept of wave amplitude. The discussion also covers the Fourier transform theorem, which allows for the reconstruction of a function from its wave components.
🤔 Properties and Representation of the Delta Function
This part explores the properties of the Delta function, a key concept in quantum mechanics. It discusses the intuitive definition of the Delta function as an infinite, narrow function with an area of one. The paragraph outlines the properties of the Delta function, including its behavior under integration and its use in representing the operation on a function. It also presents a theorem that provides a representation of the Delta function in terms of Fourier transforms.
🚀 Quantum States and the Heisenberg Uncertainty Principle
The speaker introduces the concept of describing the state of a quantum mechanical particle using an orthonormal basis of states. It contrasts this with classical mechanics, where both position and momentum are known. In quantum mechanics, due to the Heisenberg uncertainty principle, one can only know either position or momentum, but not both simultaneously. The paragraph also discusses the eigenvectors of position and their use in constructing wavefunctions.
🌌 Wave-Particle Duality and Quantum Description
This section discusses the duality in quantum mechanics where a particle can be described by either its position or momentum, but not both. It explains the concept of wavefunctions as projections of a state onto a state of definite position and how these wavefunctions can be used to calculate probabilities. The paragraph also touches on the normalization of quantum states and the role of the Dirac Delta function in continuous variable systems.
🤓 Momentum Eigenvectors and Operators
The paragraph explores the concept of momentum in quantum mechanics, introducing the momentum operator and its action on wavefunctions. It discusses the eigenvectors of the momentum operator and their relationship to the observable values of momentum. The speaker also explains the mathematical form of these eigenvectors and how they relate to the wavelength of a particle, hinting at the de Broglie wavelength concept.
🌟 Wavefunctions of Particles with Definite Momentum
This section focuses on the wavefunctions of particles with definite momentum, noting their oscillatory nature and the fact that they are delocalized. It discusses the concept of a momentum space wavefunction and how it is related to the probability amplitude for finding different momenta. The paragraph also explains how to calculate the momentum space wavefunction using the Fourier transform of the position space wavefunction.
🔍 Uncertainty Principle and Hamiltonians
The speaker touches on the uncertainty principle, relating it to Fourier transforms and the behavior of conjugate variables like position and momentum. It also introduces the concept of Hamiltonians in quantum mechanics, which govern the time evolution of state vectors and are related to the classical idea of energy. The paragraph sets the stage for a deeper exploration of quantum mechanical evolution and the Hamiltonian's role.
🚦 Time Evolution and Simple Hamiltonians
This part discusses the time-dependent Schrödinger equation and its implications for the evolution of quantum states. It explores simple Hamiltonians and their effects on wavefunctions, illustrating how different Hamiltonians can lead to different behaviors of quantum states over time. The speaker also draws parallels between quantum and classical mechanics, particularly in the context of the Hamiltonian's role in system evolution.
🌉 Schrodinger Equation for Non-Relativistic Particles
The paragraph concludes with a discussion on the Schrödinger equation for a non-relativistic particle, which is a more complex scenario than the simple Hamiltonian cases previously discussed. It highlights that for such particles, the wavefunction does not maintain its shape and tends to disperse over time, contrasting with the rigid movement seen in the simpler models. The speaker also notes that this equation is a type of wave equation, with the wavefunction representing the quantum state of the particle.
Mindmap
Keywords
💡Entanglement
💡Quantum Mechanics
💡Fourier Analysis
💡Dirac Delta Function
💡Momentum
💡Wavefunction
💡Heisenberg Uncertainty Principle
💡Schrodinger Equation
💡Hamiltonian
💡Eigenvectors and Eigenvalues
💡Normalization
Highlights
Entanglement is a fundamental subject and the heart of quantum mechanics.
The foundations of quantum mechanics have been laid out through the study of simple systems.
In quantum mechanics, the simplest empirical observations involve apparatus that can measure spin and window apparatus, yielding binary outputs.
The concept of superposition allows for the combination of states, including the number of particles.
The radiation field can be modeled with a degree of freedom representing the presence or absence of a photon.
The interaction between electrons in a system aims to maximize anti-alignment, involving the emission of a photon.
Fourier analysis and the Dirac Delta function are essential mathematical tools in quantum mechanics.
The Dirac Delta function is represented as an integral over plane waves, providing a key relationship in quantum mechanics.
Quantum mechanics describes the state of a particle using position or momentum, but not both simultaneously due to the Heisenberg uncertainty principle.
The position and momentum operators in quantum mechanics are hermitian and their eigenvectors provide a basis for state description.
The wave function of a particle with definite momentum is delocalized in position, illustrating the uncertainty principle.
The momentum space wavefunction is the Fourier transform of the position space wave function, relating probability amplitudes for different momenta.
The Hamiltonian for a simple quantum system can be a constant times the momentum, leading to solutions where the wave function moves without changing shape.
The expectation value of position for a quantum system with a simple Hamiltonian moves with a uniform velocity.
The Hamiltonian for a non-relativistic particle is typically given by P squared over 2m, representing a free particle without forces acting on it.
The Schrodinger equation for a non-relativistic particle results in a wave equation where the wave function can spread out over time.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: