2019 AP Calculus AB FRQ #2
TLDRIn this educational video, Alan from Bothell STEM dives into the 2019 AP Calculus AB free response question number two. He begins by discussing the velocity of a particle moving along the x-axis, represented by a differentiable function V(P), and uses the Mean Value Theorem to justify the existence of a time T where the acceleration (V'(P)) equals zero. Alan then employs the trapezoid rule to approximate the displacement of particle P. Subsequently, he addresses the velocity and displacement of particle Q, using calculus to find the time interval where the velocity of particle Q is at least 60 meters per hour and calculating the distance traveled by particle Q during this interval. Finally, he approximates the distance between particles P and Q at time T equals 2.8, using initial positions and displacements derived from earlier parts of the problem. The video is a comprehensive walkthrough of calculus concepts applied to a physics problem, catering to viewers interested in AP Calculus.
Takeaways
- 📚 Alan is discussing AP Calculus AB free response questions from 2019, focusing on question number two.
- 🚀 The velocity of particle P is given by a differentiable function V(P), where V is in meters per hour and T is in hours.
- 📈 A table of selected values for V(P) of T is provided, and particle P starts at the origin at time T=0.
- 🔍 The task is to justify that there must be at least one time T between two given points where the acceleration (V'(P)) equals zero, using the Mean Value Theorem.
- 🤓 The Mean Value Theorem is applicable because V(P) is given as differentiable, which is a requirement for the theorem.
- 📐 The theorem is used to find a time C where the acceleration equals the average rate of change between the two given points, which is calculated to be zero.
- 📊 A trapezoid sum with three subintervals is used to approximate the value of the displacement of particle P.
- 🔢 The approximate displacement is calculated to be 40.75 meters, which represents the area under the velocity curve.
- 🛤️ Particle Q also moves along the x-axis with a given velocity function, and the task is to find the time interval and distance traveled when the velocity is at least 60 meters per hour.
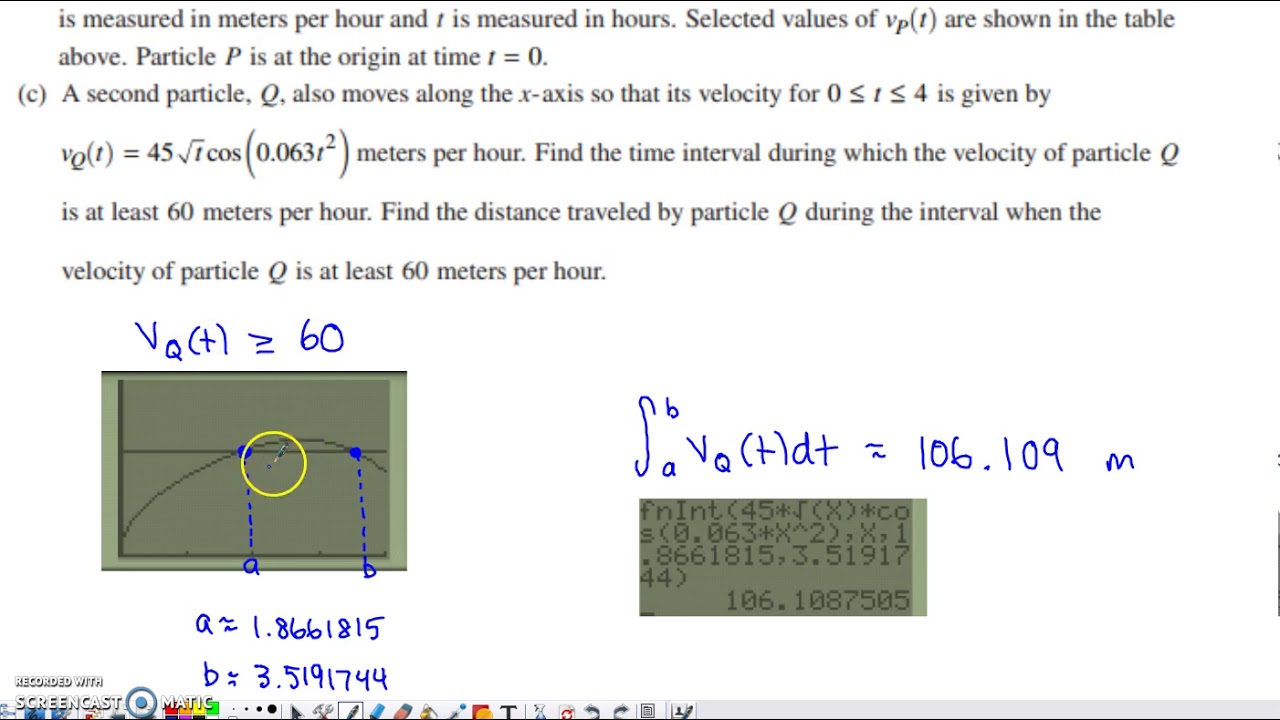
- ⏱️ The time interval is found by solving for when the velocity of Q is greater than 60, yielding two time points at approximately 1.866 and 3.519 hours.
- 📏 The distance traveled by particle Q during the time interval of at least 60 meters per hour is calculated to be 106.1 meters.
- 📍 At time T=0, particle Q is at position -90, and by integrating the velocity function from T=0 to T=2.8 and adding the initial position, the approximate position of Q is found to be 45.938 meters.
- 🔗 The distance between particles P and Q at time T=2.8 is calculated by subtracting the displacement of P from the position of Q, resulting in approximately 5.1918 meters.
Q & A
What is the topic of the video discussed by Alan?
-The video is about analyzing AP Calculus AB free response questions from the year 2019, specifically focusing on question number two.
What is the velocity function given for particle P?
-The velocity function for particle P is denoted as V(P), where V(P) is measured in meters per hour and T is measured in hours.
What mathematical theorem is used to justify the existence of at least one time T where the acceleration of particle P equals zero?
-The Mean Value Theorem is used to justify the existence of such a time T.
What is the condition that must be met for the Mean Value Theorem to be applicable?
-The function must be differentiable over the interval in question. In the script, it is confirmed that V(P) is differentiable.
How is the trapezoid rule used to approximate the value of the integral in the script?
-The trapezoid rule is used by averaging the y-values and multiplying by the interval width. In the script, it is applied over three subintervals to approximate the displacement of particle P.
What is the velocity function for particle Q given in the script?
-The velocity function for particle Q is given as v(t) = 4√(cos(0.03t^2)).
How does Alan determine the time interval where the velocity of particle Q is at least 60 meters per hour?
-Alan determines the time interval by plotting the velocity function and subtracting 60 from it to find when the velocity exceeds 60 meters per hour.
What is the integral used for in the context of finding the distance traveled by particle Q?
-The integral is used to calculate the distance traveled by particle Q over the time interval where its velocity is at least 60 meters per hour.
How does Alan approximate the position of particle Q at time T equals zero?
-Alan uses the initial position of particle Q, which is at -90, and the displacement over the given time interval to approximate its position.
What is the approximate distance between particle P and particle Q at time T equals 2.8?
-The approximate distance between particle P and particle Q at time T equals 2.8 is 5.1918 meters.
What is the significance of the Mean Value Theorem in this context?
-The Mean Value Theorem is significant because it guarantees the existence of a time C within a given interval where the instantaneous rate of change (acceleration) equals the average rate of change (secant line slope), which is zero in this case.
How does Alan ensure that the integral for the distance traveled by particle Q is always positive?
-Alan ensures that the integral is always positive by considering the absolute value of the velocity function V(Q) of T, since the velocity is always over sixty meters per hour and hence positive.
Outlines
📚 Mean Value Theorem and Trapezoid Rule in AP Calculus
In this paragraph, Alan from Bothell STEM introduces viewers to AP Calculus AB free response questions, focusing on question number two from the 2019 exam. The discussion revolves around the velocity of particle P along the x-axis, represented by a differentiable function V(P, T), with V measured in meters per hour and T in hours. A table of selected values for V(P, T) is provided, and it's established that particle P starts at the origin at T=0. Alan uses the Mean Value Theorem to justify the existence of a time T where the acceleration (V'(T)) equals zero, by comparing the velocity at T=3 and T=2.8. He then employs the trapezoid rule to approximate the displacement of particle P, which involves averaging y-values and multiplying by the interval width. The process is illustrated with a step-by-step calculation, resulting in an approximate displacement of 40.75 meters.
🚀 Calculating Velocity and Displacement for Particle Q
The second paragraph delves into the motion of particle Q, which also moves along the x-axis with a velocity function given by V(Q, T) ≤ 4. The task is to find the time interval during which the velocity of particle Q is at least 60 meters per hour and to calculate the distance traveled by particle Q during this interval. Alan plots the velocity function and identifies the times when the velocity exceeds 60 m/h, which are T=1.866 and T=3.519. He then sets up an integral from 1.866 to 3.519 to find the distance traveled, which is approximately 106.1 meters. Additionally, using information from a previous part of the problem, Alan approximates the distance at time T=2.8 by integrating the function for particle Q's position from T=0 to T=2.8, adjusting for the initial position of particle Q at -90 meters. The final position is calculated to be approximately 45.938 meters, and by comparing this with particle P's displacement, the distance between the two particles at that time is determined to be 5.1918 meters.
Mindmap
Keywords
💡AP Calculus
💡Velocity
💡Acceleration
💡Mean Value Theorem
💡Trapezoid Rule
💡Displacement
💡Particle Q
💡Integration
💡Position
💡Distance Traveled
💡Differentiable Function
Highlights
Alan from Bothell STEM is discussing the 2019 AP Calculus AB free response question number two.
The velocity of particle P is given by a differentiable function V(P) with respect to time T.
Values for V(P) at selected times are provided in a table.
Particle P starts at the origin at time T equals zero.
The task is to justify the existence of at least one time T where the acceleration V'(P) equals zero using the Mean Value Theorem.
The Mean Value Theorem is applicable because V(P) is differentiable, which is a given condition.
A trapezoid sum with three subintervals is used to approximate the value of displacement for particle P.
The trapezoid rule involves averaging y-values and multiplying by the interval width.
The approximate displacement is calculated to be 40.75 meters.
Particle Q moves along the x-axis with a given velocity function and the task is to find the time interval where its velocity is at least 60 meters per hour.
The time interval is found by plotting the velocity function and looking for the zeros where the velocity exceeds 60 meters per hour.
The first time this occurs is at T equals 1.866 and the second time at T equals 3.519.
The distance traveled by particle Q during the time interval of at least 60 meters per hour is calculated using integration.
The integral results in a distance of 106.1 meters for particle Q.
Particle Q starts at a position of negative 90 meters, and its position at time T equals 2.8 is approximated using integration and previous results.
The approximate position of particle Q at time T equals 2.8 is 45.938 meters.
The distance between particle P and Q at time T equals 2.8 is calculated to be 5.1918 meters.
The video concludes with an invitation for viewers to share their experiences or ask questions about the problem.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: