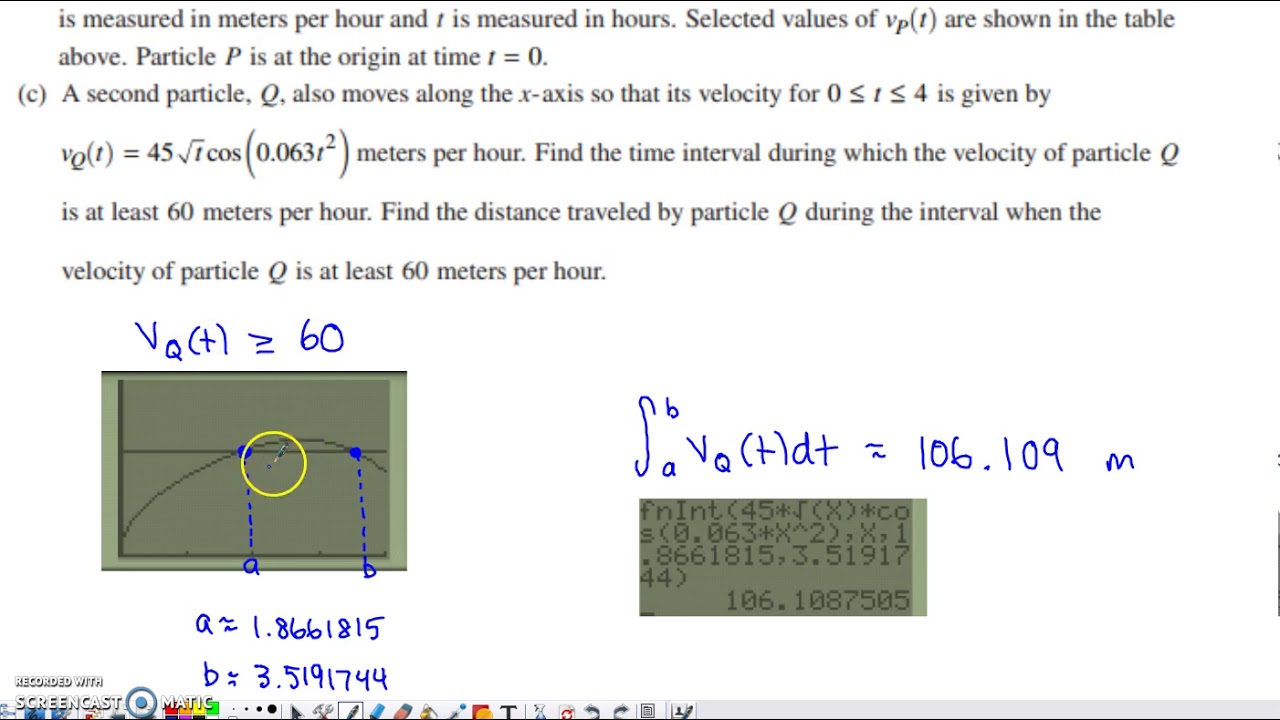
2021 AP Calculus AB Free Response #2 (First Administration)
TLDRThe video script presents a physics problem involving two particles, P and Q, moving along the x-axis with given initial positions and velocities. The problem is to find their positions at time equals one and determine if they are moving towards or away from each other. The presenter uses calculus to solve the problem, performing integrals to find the positions and the derivative to find the acceleration of particle Q. The script also discusses the concept of velocity and acceleration, explaining that particles are moving towards each other if they have velocities in opposite directions. Finally, the presenter calculates the total distance traveled by particle P using an integral with the absolute value to ensure the result represents distance, not displacement. The video is an educational walkthrough that engages viewers in understanding the principles of motion and the application of calculus in physics.
Takeaways
- 📐 The problem involves finding the positions of two particles, P and Q, moving along the x-axis at time t equals 1, given their initial positions and velocity functions.
- 🚀 Particle P starts at position x=5 with an unspecified velocity function, while Particle Q starts at position x=10 with a different velocity function.
- ⌛ To find the positions at time t=1, the integral of the velocity function from t=0 to t=1 is used for each particle, accounting for their initial positions.
- 🧮 The integrals for Particle P and Q are calculated using a calculator, with the results being 5.371 for P and 8.564 for Q.
- 🔍 The direction of movement for each particle is determined by evaluating their velocities at time t=1, with Particle P moving to the right and Particle Q moving to the left.
- 🤖 The particles are moving towards each other at time t=1 since Particle Q is on the right and moving left, while Particle P is on the left and moving right.
- 📉 To find the acceleration of Particle Q, the derivative of its velocity function is taken and evaluated at t=1, resulting in an acceleration of 1.027.
- ↔️ The sign of acceleration and velocity for Particle Q indicates whether the particle is speeding up or slowing down; in this case, it is slowing down as they have different signs.
- 📏 The total distance traveled by Particle P is found by integrating the absolute value of its velocity function from 0 to π, resulting in a distance of 1.931.
- 🛠️ The use of a calculator simplifies the process of entering complex expressions and performing multiple calculations, reducing the chance of errors.
- 📈 The process can be verified by graphing the velocity functions to visually confirm the movements and calculations of the particles.
- 💡 The script emphasizes the importance of correctly entering the initial data and performing the integrals to ensure accurate results for the problem at hand.
Q & A
What is the initial position of particle p on the x-axis?
-The initial position of particle p on the x-axis is 5 units when time t equals zero.
What is the initial position of particle q on the x-axis?
-The initial position of particle q on the x-axis is 10 units when time t equals zero.
How are the positions of particles p and q at time t equals 1 found?
-The positions are found by integrating the velocity functions from time 0 to 1 and adding the initial positions of the particles.
What is the integral of the velocity function for particle p from time 0 to 1?
-The integral of the velocity function for particle p from time 0 to 1 is calculated to be 5.371 units.
What is the integral of the velocity function for particle q from time 0 to 1?
-The integral of the velocity function for particle q from time 0 to 1 is calculated to be 8.564 units.
In which direction is particle p moving at time t equals 1?
-At time t equals 1, particle p is moving to the right since its velocity at that time is positive.
In which direction is particle q moving at time t equals 1?
-At time t equals 1, particle q is moving to the left since its velocity at that time is negative.
Are particles p and q moving towards or away from each other at time t equals 1?
-Particles p and q are moving towards each other at time t equals 1 because particle p has a positive velocity (moving right) and particle q has a negative velocity (moving left).
How is the acceleration of particle q at time t equals 1 calculated?
-The acceleration of particle q at time t equals 1 is found by taking the derivative of the velocity function and evaluating it at t equals 1.
What is the acceleration of particle q at time t equals 1?
-The acceleration of particle q at time t equals 1 is calculated to be 1.027 units.
Is the speed of particle q increasing or decreasing at time t equals 1?
-The speed of particle q is decreasing at time t equals 1 because the acceleration is positive and the velocity is negative, indicating it is slowing down.
How is the total distance traveled by particle p calculated?
-The total distance traveled by particle p is found by integrating the absolute value of its velocity function from time 0 to pi.
What is the total distance traveled by particle p from time 0 to pi?
-The total distance traveled by particle p from time 0 to pi is calculated to be 1.931 units.
Outlines
🔍 Calculating Particle Positions and Velocities
The first paragraph of the script discusses a physics problem involving finding the positions of two particles, P and Q, at a specific time t=1. The particles are moving along the x-axis with given initial positions and velocity functions. The presenter uses integration to find the positions at time t=1, starting from the initial positions and adding the change in position, which is the integral of the velocity function over time. The integrals are calculated using a calculator, with the initial positions for P and Q being 5 and 10, respectively. The final calculated positions are 5.371 for particle P and 8.564 for particle Q. The presenter also discusses the direction of the particles' movement by calculating their velocities at time t=1, determining that particle P is moving to the right and particle Q to the left, indicating they are moving towards each other.
📐 Finding Acceleration and Distance Traveled
The second paragraph focuses on calculating the acceleration of particle Q and the total distance traveled by particle P. The acceleration is found by taking the derivative of the velocity function for particle Q and evaluating it at t=1. The presenter uses a calculator to find the acceleration, which is 1.027, indicating that the speed of particle Q is increasing at time t=1 as the acceleration and velocity have different signs, suggesting the particle is slowing down. To find the total distance traveled by particle P, the presenter integrates the absolute value of the velocity function from 0 to π, which represents the total distance regardless of direction. The final calculated distance is 1.931. The paragraph concludes with a suggestion to graph the functions to verify the calculations.
Mindmap
Keywords
💡Free response question
💡Particle
💡Velocity
💡Position
💡Integral
💡Calculator
💡Velocity function
💡Acceleration
💡Direction
💡Distance
💡Absolute value
Highlights
The task involves solving for the positions of two particles, p and q, at time t equals 1 on the x-axis.
Particle p's initial position is given as x equals 5 at time t equals 0.
Particle q's initial position is x equals 10 at time t equals 0.
The velocity of particle p is represented by a sine function of time t to the power of 1.5.
The velocity of particle q is represented by a function involving t, x, and an exponential term.
The integral from time 0 to 1 of the velocity function is used to find the change in position.
The final positions of particles p and q at time t equals 1 are calculated using integration and initial positions.
The calculated position for particle p at time t equals 1 is 5.371.
The calculated position for particle q at time t equals 1 is 8.564.
To determine if the particles are moving towards or away from each other, their velocities at time t equals 1 are examined.
Particle p has a positive velocity at time t equals 1, indicating it is moving to the right.
Particle q has a negative velocity at time t equals 1, indicating it is moving to the left.
Since particle q is to the right and both particles are moving towards each other, their velocities and positions are analyzed.
The acceleration of particle q is found by taking the derivative of its velocity function at time t equals 1.
The acceleration of particle q at time t equals 1 is calculated to be 1.027.
The velocity and acceleration of particle q have different signs, indicating the particle is slowing down.
The total distance traveled by particle p is calculated by integrating the absolute value of its velocity function from 0 to pi.
The calculated total distance traveled by particle p is 1.931.
The process involves using a calculator for complex mathematical operations to ensure accuracy.
The transcript suggests the possibility of graphing the functions to visually confirm the calculations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: