Calorimetry Problems, Thermochemistry Practice, Specific Heat Capacity, Enthalpy Fusion, Chemistry
TLDRThe video script offers a detailed exploration of various thermodynamic problems involving heat energy calculations. It begins with calculating the energy required to heat water from 26°C to 48°C using the specific heat capacity formula (q = mcΔT), resulting in 7,363.8 joules. The script then addresses the energy needed to melt ice, highlighting the use of the heat of fusion and the importance of unit consistency. A calorimetry problem involving a metal and water mixture is solved to find the metal's specific heat capacity. The final temperature of a mixture of iron and water is calculated, emphasizing the role of specific heat capacities in determining temperature changes. The enthalpy change of dissolving calcium chloride in water is calculated, revealing the reaction's exothermic nature. Lastly, the script calculates the total energy required to transform 24 grams of ice at -20°C into steam at 250°C, involving multiple phase changes and specific heat capacities for ice, water, and steam. The total energy absorbed is 805,534.7 joules, with the majority used in vaporization. The script serves as an educational guide on heat energy calculations in different scenarios.
Takeaways
- 🔍 To calculate the heat energy required to heat water, use the equation q = mcΔT, where m is mass, c is specific heat capacity, and ΔT is the change in temperature.
- 🧊 The specific heat capacity of water is 4.184 joules per gram per celsius, indicating the energy needed to raise the temperature of 1 gram of water by 1 degree Celsius.
- 🧑🔬 For phase change problems like melting ice, use the equation q = mΔH, where ΔH is the heat of fusion, and ensure that units for q are in joules.
- 📉 When calculating the specific heat capacity of a metal, consider the heat transfer between the metal and water, and use the equation with appropriate signs to account for temperature changes.
- 🔥 The final temperature in a mixture of substances at different temperatures is influenced by their specific heat capacities and masses.
- 🌡️ The specific heat capacity of water is higher than that of most metals, leading to smaller temperature changes in water for the same amount of heat energy.
- 📚 In a calorimetry problem, the heat released by a substance is equal to the heat absorbed by another, and this principle is used to find unknown specific heat capacities or enthalpy changes.
- 🔄 When a reaction is endothermic for the surroundings (like water absorbing heat), it is exothermic for the reaction itself, as seen in the temperature change of the solution.
- ⚖️ To find the enthalpy change of a reaction, convert the mass of the reactants to moles and use the formula ΔH = q/n, where q is the heat energy and n is the number of moles.
- 🧪 For complex thermal processes like heating ice to steam, break down the process into stages (temperature change, phase change, etc.) and calculate the heat energy for each stage.
- 🔥 Most of the energy in heating ice to steam is used in the phase change from water to steam, highlighting the high energy requirement for vaporization.
- 🧠 Understanding the principles of specific heat capacities, phase changes, and heat energy calculations is crucial for solving thermodynamics problems in chemistry.
Q & A
What is the formula to calculate the heat energy required for a temperature change?
-The formula to calculate the heat energy (q) required for a temperature change is q = mcΔT, where m is the mass, c is the specific heat capacity, and ΔT is the change in temperature.
How much energy is required to heat 80 grams of water from 26°C to 48°C, given the specific heat capacity of water is 4.184 J/g°C?
-The energy required is calculated as follows: q = (80 g) × (4.184 J/g°C) × (48°C - 26°C) = 7,363.6 J.
What is the heat of fusion, and how is it used in calculating the energy required to melt ice?
-The heat of fusion is the amount of energy required to change a unit mass of a substance from solid to liquid without changing its temperature. It is used in the equation q = mΔH_fusion, where m is the mass of the ice and ΔH_fusion is the heat of fusion for ice.
How do you calculate the specific heat capacity of a metal when a known mass of it is cooled in a known mass of water?
-You use the principle of conservation of energy, where the heat lost by the metal equals the heat gained by the water. You set up the equation considering the specific heat capacity of water and solve for the unknown specific heat capacity of the metal.
What is the final temperature when 100 grams of iron at 95°C is placed in 200 grams of water at 25°C?
-Using the principle of heat transfer, the final temperature is calculated by setting up an equation that equates the heat lost by the iron to the heat gained by the water. The final temperature is found to be 28.57°C.
How do you determine if a reaction is endothermic or exothermic based on the temperature change of the solution?
-If the temperature of the solution increases, it indicates that the reaction is exothermic (releasing heat). Conversely, if the temperature decreases, the reaction is endothermic (absorbing heat).
What is the enthalpy change of a reaction when given the temperature change of water?
-The enthalpy change (ΔH) is calculated by dividing the heat absorbed or released by the water (q) by the moles of the solute (n). The heat q is found using the equation q = mcΔT, and the moles are calculated from the mass and molar mass of the solute.
How much energy is required to heat 24 grams of ice at -20°C to steam at 250°C?
-The total energy required is the sum of the energy required to raise the temperature of ice to 0°C (q1), the energy to melt the ice (q2), the energy to heat water to 100°C (q3), the energy to vaporize water to steam (q4), and the energy to heat steam to 250°C (q5). Each step uses the respective specific heat capacities and phase change enthalpies.
Why is the majority of the energy required to convert ice at -20°C to steam at 250°C used in the vaporization process?
-The vaporization process requires a significant amount of energy because it involves changing the phase of water from liquid to gas, which is an endothermic process with a high enthalpy of vaporization.
What is the significance of specific heat capacity in determining the final temperature of a mixture of substances at different temperatures?
-The specific heat capacity determines how much heat energy is required to raise the temperature of a substance. A substance with a higher specific heat capacity will experience a smaller temperature change for a given amount of heat energy, which influences the final equilibrium temperature when substances are mixed.
How do you calculate the heat energy absorbed or released by a water sample when a metal is cooled in it?
-The heat energy absorbed by the water sample is calculated using the equation q = mcΔT, where m is the mass of the water, c is the specific heat capacity of water, and ΔT is the change in temperature of the water.
Outlines
🔥 Heating Water: Energy Calculation
This paragraph explains how to calculate the energy required to heat water from 26°C to 48°C using the formula q = mcΔT, where m is the mass, c is the specific heat capacity, and ΔT is the change in temperature. It provides the values for the mass of water (80 grams), the specific heat capacity (4.184 J/g°C), and the temperature change (22°C). The calculation results in 7,363.8 joules needed to perform the heating. The paragraph also introduces the concept of the specific heat capacity of water and transitions into the next problem regarding the energy required to melt ice.
🧊 Melting Ice: Phase Change Energy
The second paragraph deals with the energy required to melt 75 grams of ice, given the heat of fusion for ice. It contrasts the temperature change problem with a phase change problem, emphasizing the use of the formula q = mΔHfus, where m is the mass and ΔHfus is the heat of fusion per gram. The calculation involves multiplying the mass of ice (75 grams) by the heat of fusion (334 J/g), resulting in 25,350 joules needed to melt the ice. It also discusses the heat transfer between a hot metal chunk and water, leading to a final temperature of 28°C, and the method to calculate the specific heat capacity of the metal.
🔩 Specific Heat Capacity of Metal
This paragraph focuses on calculating the specific heat capacity of a metal when a 70-gram piece at 180°C is placed into 400 grams of water at 25°C, resulting in a final temperature of 28°C. It uses the principle of conservation of energy, stating that the heat lost by the metal equals the heat gained by the water. The calculation involves the specific heat capacity of water (4.184 J/g°C) and the temperature changes for both the metal and water. By solving the equation, the specific heat capacity of the metal is found to be 0.472 J/g°C.
🌡️ Final Temperature of Iron and Water Mixture
The fourth paragraph addresses a scenario where 100 grams of iron at 95°C is placed into 200 grams of water at 25°C, and the final temperature of the mixture is to be determined. It explains that the final temperature will be between the initial temperatures of the iron and water, and it is likely closer to the temperature of the water due to water's higher specific heat capacity. The calculation involves the specific heat capacities of iron (0.45 J/g°C) and water (4.184 J/g°C) and their respective masses and temperature changes. The final temperature is calculated to be 28.57°C.
⚗️ Enthalpy Change of Calcium Chloride Dissolution
This paragraph describes the process of calculating the enthalpy change when 2.6 grams of calcium chloride is dissolved in 260 grams of water, resulting in a temperature increase from 23°C to 26.4°C. It outlines that the enthalpy change is typically given in kilojoules per mole and can be estimated by dividing the heat of the reaction (q) in kilojoules by the number of moles (n). The heat absorbed by the water is calculated using the formula q = mcΔT, resulting in 3,698.7 J. Since the reaction is exothermic, the heat of the reaction is negative, and the molar mass of calcium chloride is used to convert grams to moles. The final enthalpy change is calculated to be -157.09 kJ/mol.
🌟 Heating Ice to Steam: Multi-Stage Energy Calculation
The final paragraph details the process of calculating the total energy required to heat 24 grams of ice from -20°C to steam at 250°C. It involves a multi-stage process with five separate calculations: q1 for heating ice to 0°C, q2 for melting ice to water, q3 for heating water to 100°C, q4 for vaporizing water to steam, and q5 for heating steam to 250°C. Each stage uses different specific heat capacities and phase change enthalpies. The total heat absorbed is the sum of these five q values, resulting in a total of 80,534.7 joules, with the majority of energy (54,266.7 joules) required for the vaporization of water.
Mindmap
Keywords
💡Specific Heat Capacity
💡Heat of Fusion
💡Heat of Vaporization
💡Thermal Equilibrium
💡Endothermic Process
💡Exothermic Process
💡Enthalpy Change
💡Phase Change
💡Calorimetry
💡Heat Transfer
💡Temperature Change
💡Energy Calculation
Highlights
The equation q = mCΔT is used to calculate the heat energy required for a temperature change.
The specific heat capacity of water is 4.184 J/g°C, indicating the energy needed to raise the temperature of 1 gram of water by 1°C.
For phase change problems like melting ice, the equation q = mΔHf (mass times heat of fusion) is used.
When a hot metal is placed in cold water, heat flows from the metal to the water until thermal equilibrium is reached at a final temperature.
The specific heat capacity of a metal can be calculated by equating the heat lost by the metal to the heat gained by the water.
The final temperature when mixing substances at different temperatures depends on their specific heat capacities and masses.
Water has a higher specific heat capacity than metals like iron, so it experiences smaller temperature changes.
The enthalpy change of a reaction can be calculated from the heat absorbed or released by the solution and the moles of reactant.
An endothermic reaction absorbs heat, causing the solution temperature to decrease, while an exothermic reaction releases heat, raising the temperature.
The total heat required to change a substance's state from one extreme to another involves calculating multiple q values for different stages.
Most of the energy when converting ice to steam goes into the phase change from liquid water to steam.
The specific heat capacities for ice, water, and steam are 2.03, 4.184, and 2.01 J/g°C respectively.
The heat of fusion for ice is 334 J/g and the heat of vaporization for water is 40.7 kJ/mol.
To convert between grams and moles, divide the mass in grams by the molar mass of the substance.
When calculating enthalpy change, convert joules to kilojoules by dividing by 1000.
The total heat required for a substance to undergo multiple state changes can be found by summing the individual q values.
This method of calculating heat energy and enthalpy changes has practical applications in thermodynamics and calorimetry.
Transcripts
Browse More Related Video

Latent Heat of Fusion and Vaporization, Specific Heat Capacity & Calorimetry - Physics

Specific heat, heat of fusion and vaporization example | Chemistry | Khan Academy

How Much Thermal Energy Is Required To Heat Ice Into Steam - Heating Curve Chemistry Problems

Chilling water problem | States of matter and intermolecular forces | Chemistry | Khan Academy
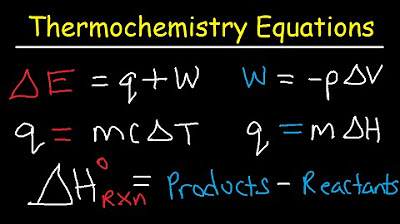
Thermochemistry Equations & Formulas - Lecture Review & Practice Problems

Heats of Fusion & Vaporization
5.0 / 5 (0 votes)
Thanks for rating: