Latent Heat of Fusion and Vaporization, Specific Heat Capacity & Calorimetry - Physics
TLDRThis educational script delves into the principles of heat energy in physics, focusing on two key equations: Q = mL for phase changes and Q = mcΔT for temperature changes. It explains concepts like latent heat of fusion and vaporization, specific heat capacities of water, ice, and steam, and how these relate to energy absorption and release. The transcript walks through several problems to illustrate calculations for melting ice, heating water, and phase changes, emphasizing the high energy required for vaporization. It also discusses heat curves, energy conservation, and calorimetry, highlighting the differences in temperature changes and phase changes, and how substances with varying specific heat capacities respond to heat input.
Takeaways
- 🔍 The script discusses two key equations in physics related to heat energy: Q = mL (where Q is heat energy, m is mass, and L can be latent heat of fusion or vaporization) and Q = mcΔT (where Q is heat energy, m is mass, c is specific heat capacity, and ΔT is change in temperature).
- 🔥 Q is measured in joules (J) and can also be measured in calories, with 1 calorie being approximately 4.184 J and 1 kilocalorie (capital calorie) equal to 1000 calories.
- 🧊 The latent heat of fusion is the energy required to change a solid into a liquid without changing temperature, and the latent heat of vaporization is the energy needed to change a liquid into a gas.
- ⏱ The amount of energy required to melt 1 kg of ice is 3.33 * 10^5 J, and to vaporize 1 kg of water is about 22.6 * 10^5 J, which is significantly higher, indicating it takes much more energy to vaporize water than to melt ice.
- 🌡 The specific heat capacity (c) of liquid water is approximately 4186 J/kg°C, which means it takes 4186 J to raise the temperature of 1 kg of water by 1°C.
- ❄ For ice, the specific heat capacity is about half that of liquid water, at 2100 J/kg°C, and for steam, it's close to ice at about 2000 J/kg°C.
- 📚 The script uses problems to illustrate the application of these concepts, such as calculating the energy required to melt a certain mass of ice or to raise the temperature of water.
- 📉 The heat curve is explained, showing how temperature remains constant during phase changes (like melting or boiling) and increases during temperature changes.
- 🔁 The concept of energy conservation is discussed, explaining how heat energy goes into increasing kinetic energy during temperature changes and potential energy during phase changes.
- 🔄 The script also covers a calorimetry problem involving a metal piece and water, demonstrating how the specific heat capacity of water is much higher than that of metals, leading to smaller temperature changes in water compared to metals.
- 📊 The final calorimetry problem calculates the specific heat capacity of the metal, showing that it is significantly lower than that of liquid water, which is why metals heat up and cool down quickly.
Q & A
What are the two main equations related to heat energy discussed in the script?
-The two main equations related to heat energy discussed are Q = mL for phase changes and Q = mcΔT for temperature changes, where Q represents the amount of heat energy absorbed or released, m is the mass, L is the latent heat of fusion or vaporization, c is the specific heat capacity, and ΔT is the change in temperature.
What are the units used to measure heat energy, and how do they relate to each other?
-Heat energy is measured in joules (J) and calories. One calorie is approximately equal to 4.184 joules, and a capital calorie (kcal) is equal to 1,000 calories. Joules are more commonly used, but calories or kilo calories are also used, especially in the context of heat.
What is the latent heat of fusion, and how is it used in physics problems?
-The latent heat of fusion is the amount of energy required to change a solid into a liquid without changing its temperature, such as melting ice into water. It is used in physics problems to calculate the energy needed for phase changes, and the sign of the energy (positive or negative) indicates whether energy is being added to or removed from the system.
What is the difference between the latent heat of fusion and the latent heat of vaporization?
-The latent heat of fusion is the energy required to change a solid to a liquid, while the latent heat of vaporization is the energy needed to change a liquid to a gas. The latter requires significantly more energy than the former.
How much energy is required to melt 1 kg of ice, and what is this energy called?
-It takes 3.33 * 10^5 joules to melt 1 kg of ice. This energy is referred to as the latent heat of fusion for ice.
What is the specific heat capacity, and why is it important in understanding how substances store heat energy?
-The specific heat capacity is the amount of heat energy required to raise the temperature of 1 kg of a substance by 1°C. It is important because it indicates how much heat a substance can store without a significant change in temperature, which is useful for understanding thermal regulation and heat transfer processes.
How does the specific heat capacity of water compare to that of metals, and what does this imply about their ability to store heat?
-The specific heat capacity of water (about 4186 J/kg°C) is much higher than that of metals, which have very low specific heat capacities. This means that water can store a lot of heat energy without a significant temperature change, while metals heat up quickly when energy is added.
What is the significance of the heat curve in understanding phase changes and temperature changes?
-The heat curve helps visualize how heat energy affects the temperature and phase of a substance. It shows periods of constant temperature during phase changes (indicating energy is used to change the state rather than the temperature) and varying slopes during temperature changes (indicating the rate of temperature increase with added heat).
What is energy conservation, and how does it relate to the heating curve and phase changes?
-Energy conservation is the principle that energy cannot be created or destroyed, only transferred or changed in form. In the context of the heating curve and phase changes, it means that the energy added to a system during heating is either used to increase the temperature (increasing kinetic energy) or to change the phase of the substance (increasing potential energy).
Can you provide an example of how to calculate the total energy required to heat 7.5 kg of ice from -30°C to steam at 200°C?
-To calculate the total energy, you would need to consider multiple steps: heating the ice to 0°C, melting the ice to water, heating the water to 100°C, vaporizing the water to steam, and then heating the steam to 200°C. Each step involves different calculations based on temperature change, phase change, and the specific heat capacities or latent heats for each phase.
Outlines
🔍 Fundamental Physics Equations and Heat Energy
This paragraph introduces two key equations in physics related to heat energy: Q = m * L (where Q is the heat energy absorbed or released, m is the mass, and L could be the latent heat of fusion or vaporization) and Q = mcΔT (where Q is the energy, m is the mass, c is the specific heat capacity, and ΔT is the change in temperature). It explains the concepts of latent heat of fusion and vaporization using the example of ice melting into water and water vaporizing into steam, with specific numerical values for these processes in water. The paragraph also discusses the units of energy measurement, such as joules and calories, and their conversions.
📚 Solving Physics Problems Involving Phase Changes and Temperature Changes
This section delves into practical problem-solving in physics, focusing on phase changes and temperature changes. It demonstrates how to calculate the energy required to melt ice and raise the temperature of water using the equations introduced earlier. The paragraph provides step-by-step calculations for melting 450 grams of ice, heating 5 kg of water from 20°C to 55°C, and converting 3 kg of ice at 0°C to water at 30°C. It emphasizes the importance of understanding when to use each equation and the significance of the latent heat of fusion and specific heat capacity in these calculations.
📉 Understanding Heat Curves and Phase Changes
The paragraph explains the concept of heat curves, illustrating how temperature changes with the addition of heat energy during phase transitions. It describes the process of ice melting into water and water vaporizing into steam, highlighting the constant temperature periods during these phase changes. The heat curve graph is used to visually represent these concepts, showing different slopes and horizontal lines that correspond to temperature increases and phase transitions. The latent heat of fusion and vaporization for water is discussed in the context of the graph, with an explanation of why the line for vaporization is much longer, indicating the greater energy required for this process.
🔥 Energy Conservation and Phase Changes
This section discusses energy conservation in the context of temperature changes and phase transitions. It explains how heat energy is transferred to kinetic energy when the temperature of a substance increases and how energy is used to change the potential energy of a substance during a phase change. The paragraph uses the analogy of gravitational potential energy to clarify the concept of potential energy in molecular bonds. It also explains how the input of energy is required to separate atoms or molecules, which is then released when they come back together.
🌡 Complex Energy Calculations for Phase Changes and Temperature Shifts
The paragraph presents a complex problem involving the heating of 7.5 kg of ice from -30°C to steam at 200°C. It breaks down the problem into five separate energy calculations (Q1 to Q5) corresponding to different stages of the process: heating ice, melting ice, heating liquid water, vaporizing water, and heating steam. Each stage requires a different approach and equation, reflecting the specific heat capacities and latent heats associated with each phase change. The paragraph emphasizes the large amount of energy needed to vaporize liquid water into steam, which is a key factor in the body's cooling mechanism through sweating.
🧪 Calorimetry Problem: Metal and Water Temperature Exchange
This section introduces a calorimetry problem where a hot piece of metal is dropped into a beaker of water, leading to a heat exchange between the metal and the water. The goal is to determine the specific heat capacity of the metal. Using the conservation of energy principle, the paragraph guides through the calculations, taking into account the initial and final temperatures of both the metal and the water, and their respective masses. The result shows that the specific heat capacity of the metal is significantly lower than that of water, illustrating the concept that substances with low specific heat capacities experience large temperature changes with the same amount of heat exchange.
Mindmap
Keywords
💡Heat Energy
💡Latent Heat
💡Specific Heat Capacity
💡Phase Change
💡Temperature Change
💡Calorimetry
💡Kinetic Energy
💡Potential Energy
💡Energy Conservation
💡Heat Curve
Highlights
Q is equal to M * L and Q is equal to MCAT, two fundamental equations in physics for heat energy transfer.
Q represents the amount of heat energy absorbed or released, measured in Joules or calories.
1 calorie equals approximately 4.184 Joules, with capital and lowercase calories indicating different magnitudes.
The latent heat of fusion and vaporization are key concepts for phase changes in physics.
3.33 * 10^5 Joules per kilogram is required to melt ice, illustrating the energy needed for phase change.
The latent heat of vaporization for water is about 22.6 * 10^5 Joules per kilogram, showing the energy difference between melting and vaporizing.
The specific heat capacity (C) is crucial for temperature change calculations, with water's value being approximately 4186 Joules per kilogram per Celsius.
Water's high specific heat capacity allows it to store a significant amount of heat energy with minimal temperature change.
The specific heat capacity of ice is about half that of liquid water, at 2100 Joules per kilogram per Celsius.
Calculating energy required to melt a specific mass of ice using the latent heat of fusion.
Raising the temperature of water requires energy calculations based on mass, specific heat capacity, and temperature change.
Total energy required to convert ice at 0°C to water at 30°C involves both phase change and temperature change calculations.
Heat curves illustrate the relationship between heat added and temperature changes during phase transitions.
The latent heat of vaporization is significantly higher than that of fusion, affecting the length of heat curve segments.
Specific heat capacity and slope of temperature increase are inversely related, affecting the steepness of heat curve lines.
Energy conservation principles apply to temperature changes and phase transitions, impacting kinetic and potential energy.
A complex problem involving heating ice to steam at varying temperatures demonstrates the step-by-step energy calculation process.
Calorimetry problems, such as calculating the specific heat capacity of a metal, showcase heat transfer between substances.
The significant temperature change of the metal compared to water indicates the impact of specific heat capacity on thermal equilibrium.
Transcripts
Browse More Related Video

Calorimetry Problems, Thermochemistry Practice, Specific Heat Capacity, Enthalpy Fusion, Chemistry

Specific heat, heat of fusion and vaporization example | Chemistry | Khan Academy

Heat of Fusion and Heat of Vaporization Explained
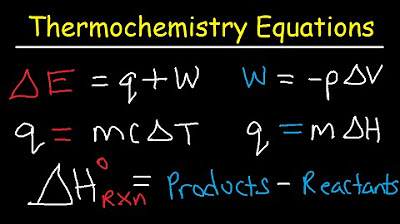
Thermochemistry Equations & Formulas - Lecture Review & Practice Problems

How Much Thermal Energy Is Required To Heat Ice Into Steam - Heating Curve Chemistry Problems

2.5 Heating/Cooling Curves (Potential and Kinetic Energy Changes)
5.0 / 5 (0 votes)
Thanks for rating: