Math 11 - Section 3.4
TLDRProfessor Monte's lecture delves into the concept of optimization, specifically focusing on finding absolute maximum and minimum values of a function. He explains the difference between relative and absolute extrema, noting that the latter refers to the highest or lowest points across the entire graph of a function. The professor uses graphs and examples to illustrate how absolute maxima and minima can occur at critical points or endpoints of a function's domain. He demonstrates the process of finding these values using calculus, emphasizing the importance of taking the derivative, setting it to zero to find critical values, and evaluating these points as well as the endpoints of a closed interval. The lecture also covers methods to determine whether a critical point corresponds to a maximum or minimum without relying on the first or second derivative tests. The application of these concepts is showcased through a problem involving advertising expenditure and sales units, highlighting the practical use of optimization in real-world scenarios. The summary underscores the significance of understanding optimization techniques for students aiming to grasp the intricacies of calculus and its applications.
Takeaways
- 📈 The concept of absolute maximum and minimum values refers to the highest or lowest points on the entire graph of a function, as opposed to relative maximum and minimum values which pertain to the highest or lowest points within a specific interval.
- 🔍 To find absolute extrema on a closed interval, one must consider critical values (where the derivative is zero or undefined) and endpoints of the interval, as absolute extrema can only occur at these points.
- 📌 When the graph of a function is defined only between two points A and B, the absolute maximum and minimum will occur either at a critical point or at one of the endpoints.
- 📘 For a closed interval, after finding the critical values, plug them and the endpoints into the original function to determine the absolute maximum or minimum by comparing the function values.
- 🤔 If a critical value is not within the interval of interest, it is disregarded when searching for the absolute maximum or minimum within that interval.
- 📐 On an open interval, if there is only one critical value, one can use the first or second derivative test to determine whether it is a relative maximum or minimum, which by default would be the absolute extremum due to the lack of other critical points.
- 🧮 The second derivative test is a useful tool to determine if a function is concave up or down, which can help identify absolute minima and maxima.
- 📉 When dealing with open intervals and a single critical value, if the second derivative is negative, the function is concave down, indicating an absolute maximum at that point.
- 🔢 In the context of optimization problems, such as maximizing profit or units sold, finding the absolute maximum can involve setting derivatives equal to zero, solving for critical points, and evaluating the function at these points and the interval endpoints.
- 💡 The process of finding absolute extrema can be applied to real-world problems, such as determining the optimal spending on advertising to maximize sales.
- ✅ Practice is key when applying calculus to find absolute maxima and minima, as it helps solidify the understanding of the concepts and methods involved.
Q & A
What is the primary focus of Section 3.4 in Professor Monte's lecture?
-Section 3.4 focuses on optimization, specifically finding absolute maximum and minimum values of a function.
How does an absolute maximum or minimum differ from a relative maximum or minimum?
-A relative maximum or minimum refers to the highest or lowest point within a specific interval, whereas an absolute maximum or minimum is the highest or lowest point across the entire domain where the function is defined.
What are the critical values in the context of finding absolute maxima and minima?
-Critical values are points where the derivative of a function is either zero or undefined. They are potential locations for absolute maxima and minima.
How can you determine if a critical point is an absolute maximum, minimum, or neither, without using the second derivative test?
-You can use the first derivative test by examining the sign of the derivative to the left and right of the critical point. If the function changes from increasing to decreasing at a critical point, it's a local maximum, and if it changes from decreasing to increasing, it's a local minimum. However, to determine if it's an absolute extremum, you would also compare the function values at the critical point and the endpoints of the interval.
What is the 'illegal move' that Professor Monte refers to when solving a cubic equation?
-The 'illegal move' is a method of factoring where you multiply both sides of an equation by a number that is not present in the equation to make the factoring process simpler. In this case, multiplying by 3 to deal with a cubic equation.
How does the process of finding absolute extrema differ when the interval is open rather than closed?
-For an open interval, you do not have endpoints to consider. If there is only one critical value in the interval, you can use the first or second derivative test to determine if it is a relative maximum or minimum, which must then also be the absolute maximum or minimum since there are no endpoints to compare with.
What is the significance of the second derivative test in determining absolute extrema?
-The second derivative test involves evaluating the sign of the second derivative at a critical point. If the second derivative is positive (concave up), the point is a local minimum, and if it is negative (concave down), the point is a local maximum. On open intervals with a single critical point, this can help determine if the point is an absolute extremum.
Why is it important to consider the domain of the function when finding critical values?
-Critical values must be within the domain of the function to be considered as potential absolute extrema. If a critical value lies outside the domain, it cannot contribute to the maximum or minimum values of the function within that domain.
How does the shape of the graph (whether it's a parabola opening upwards or downwards) influence the location of the absolute maximum or minimum?
-For a parabola that opens downwards (concave up), the vertex represents the absolute maximum value, while for a parabola that opens upwards (concave down), the vertex represents the absolute minimum value. This is because a parabola has a single maximum or minimum value.
In the context of the advertising application problem, what does 'a' represent?
-'a' represents the amount of money spent on advertising in thousands of dollars.
What is the strategy for finding the maximum number of units sold in the advertising application problem?
-The strategy involves finding the critical value within the given interval (0 to 300 in this case) and then evaluating the function at the critical value and the endpoints of the interval. The highest value obtained from these evaluations indicates the maximum number of units sold.
Outlines
📈 Introduction to Absolute Optimization
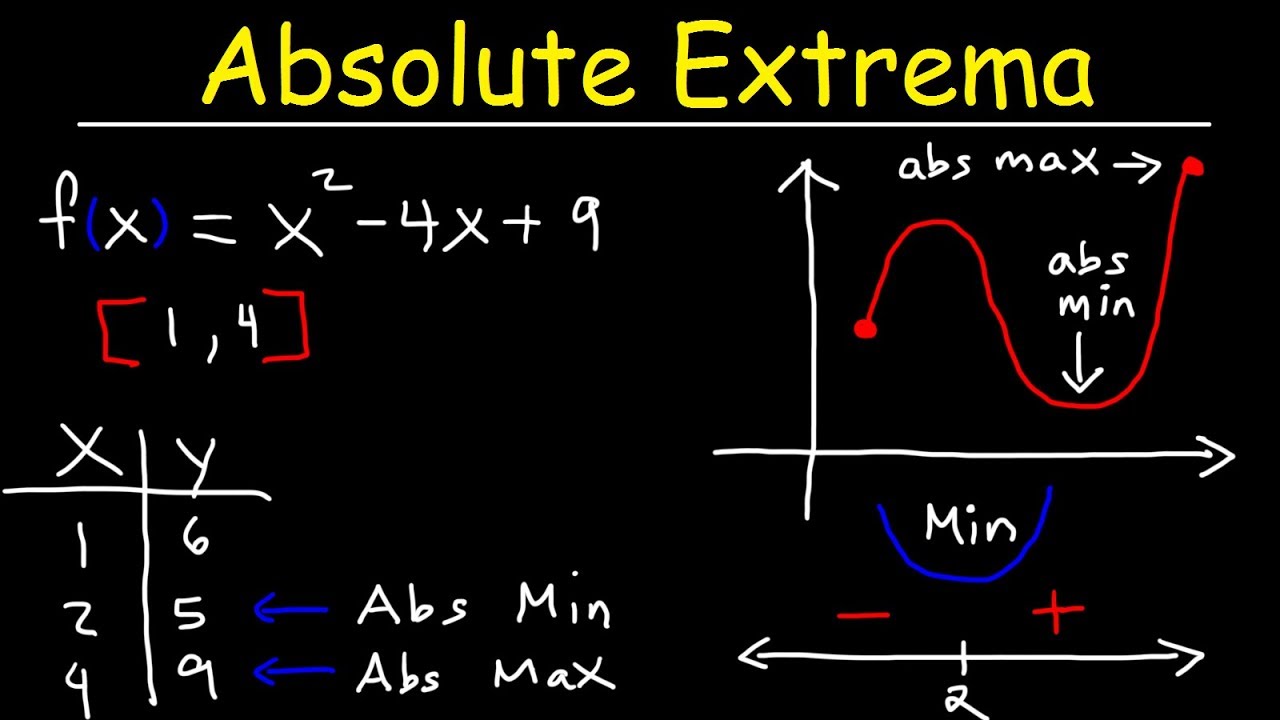
Professor Monte begins by introducing Section 3.4, focusing on optimization and the concept of absolute maximum and minimum values. Unlike relative maxima and minima, which are the highest or lowest points within an interval, absolute extrema are the highest or lowest points on the entire graph. The professor explains that these values are identified by their Y-values, as the X-values only indicate their location on the graph. The lecture includes a visual representation of a graph with an absolute maximum and minimum, and discusses critical values and endpoints in relation to absolute extrema.
📊 Absolute Max/Min on a Closed Interval
The video continues by emphasizing that absolute maximum or minimum on a closed interval can only occur at a critical value or an endpoint. The professor uses a graph to illustrate this concept and demonstrates how to find critical values by taking the derivative of the function and setting it to zero. The process of evaluating the function at critical points and endpoints to determine the absolute extrema is shown step by step, using a T-chart to compare the Y-values.
🔢 Solving for Absolute Extrema with Calculus
The third paragraph details the steps to find the absolute maximum and minimum values of a function using calculus. The professor illustrates this with an example function, finding its critical value, and then evaluating the function at the critical value and the endpoints of the given interval. The explanation includes the calculation process and emphasizes that the highest value indicates the absolute maximum, while the lowest indicates the absolute minimum.
🔍 Identifying Critical Points and Interval Endpoints
In this segment, the professor discusses the importance of considering the interval when identifying critical points. It is highlighted that if a critical point does not fall within the interval of interest, it is disregarded. The focus is on plugging the critical values and endpoints into the original function to determine the absolute maximum and minimum. The professor also clarifies the notation for expressing the results, emphasizing the function value at a given X-value.
📚 Applying the Process to a Cubic Function
The professor moves on to a new problem involving a cubic function and a closed interval. The process of finding the critical values involves setting the derivative equal to zero and solving for X. The professor uses an innovative method for factoring, referred to as the 'illegal move,' which simplifies the process. After finding the critical values, the function is evaluated at these points and the endpoints to determine the absolute extrema.
🔢 Finding Extrema on an Open Interval
The fifth paragraph explains how to find absolute extrema on an open interval, which differs from the process on a closed interval. When there's only one critical value in the interval, the professor explains using the first or second derivative test to determine if it's a maximum or minimum. The explanation includes the rationale behind these tests and how they apply to open intervals without endpoints.
📉 Determining the Shape of the Function's Graph
The sixth paragraph delves into the specifics of determining whether a critical point on an open interval represents a relative minimum or maximum, which by default is also the absolute extremum due to the lack of other critical points. The professor uses the second derivative test to confirm that a critical point is an absolute maximum because the function is concave down, indicating a peak.
📌 Applying Optimization to Real-World Scenarios
In the seventh paragraph, the professor applies the concept of absolute extrema to a real-world scenario involving advertising and sales. The goal is to find the maximum number of units that can be sold by spending a certain amount on advertising within a given budget. The process involves finding the critical point and evaluating the function at the endpoints and the critical point to identify the maximum sales volume.
📝 Wrapping Up the Lecture
The final paragraph wraps up the lecture by summarizing the key points covered. The professor reminds the students to practice finding absolute maxima and minima on both closed and open intervals, as both concepts will be tested. The lecture concludes with encouragement to keep up the hard work.
Mindmap
Keywords
💡Optimization
💡Absolute Maximum and Minimum
💡Critical Values
💡Derivative
💡First and Second Derivative Tests
💡Closed Interval
💡Open Interval
💡Endpoint
💡Quotient Rule
💡Polynomial
💡Applications in Real-World Problems
Highlights
Professor Monte introduces Section 3.4 on optimization, focusing on finding absolute maximum and minimum values.
Absolute maximum and minimum are the highest and lowest points on the entire graph of a function, as opposed to relative maximum and minimum which are within an interval.
The concept of critical values is discussed, which are points where the derivative is either zero or undefined.
An absolute maximum or minimum on a closed interval can only occur at a critical value or an endpoint.
The process of finding absolute extrema involves taking the derivative, setting it to zero, and solving for critical values within the interval.
A method to find critical values using an 'illegal move' in factoring is introduced, which simplifies the process.
The importance of considering the function's behavior at endpoints and critical points is emphasized for determining absolute extrema.
An alternative approach to finding absolute extrema on an open interval is presented, using the first or second derivative test if there's only one critical value.
The second derivative test is used to determine if a function is concave up or down, which helps in identifying absolute maxima or minima.
The first derivative test is applied to determine if a function is increasing or decreasing around a critical point to find an absolute extremum.
An example problem is solved using the first derivative test to find the absolute minimum of a function on an open interval.
The application of finding absolute extrema is demonstrated with a real-world example related to advertising and sales.
The process of taking limits as x approaches a particular value is mentioned for open intervals when there's only a single critical value.
The importance of understanding the difference between absolute and relative extrema, and how to find them on both closed and open intervals, is stressed for practical applications.
The transcript concludes with an encouragement to practice finding absolute extrema, as it will be on the test.
The method of plugging endpoints and critical values into the original function to determine the absolute maximum or minimum is summarized.
The concept of discarding critical values that are not within the interval of interest is highlighted.
The use of a T-chart to organize and compare function values at critical points and endpoints is demonstrated.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: