3.4 - Using Derivatives to Find Absolute Max and Min Values
TLDRThe video script delves into the application of first and second derivative tests to identify absolute maximum and minimum values of a function, as opposed to relative extremum values. It emphasizes that absolute extrema can occur at critical points, where the derivative is zero or undefined, or at the endpoints of a given interval. The script outlines a four-step process involving taking the first derivative, finding critical values within the interval, evaluating the function at these points and endpoints, and comparing the results to determine the absolute maximum and minimum values. The video provides step-by-step examples, including using a graphing calculator to find critical points and evaluate the function, and applies these concepts to real-world problems, such as maximizing weekly profit for an electronic store and analyzing unemployment rates over time. The script serves as a comprehensive guide to understanding and applying maximization and minimization principles in calculus.
Takeaways
- 📌 The first and second derivative tests are used to find relative maximum and minimum values, which are the highest or lowest points in relation to surrounding points on a graph.
- 🔍 Relative extremum values do not guarantee the absolute highest or lowest points over the entire domain of a function.
- 🏔️ Absolute extremum values are the highest and lowest values over a function's entire domain or a specific interval, which can occur at critical points or endpoints.
- 📈 The maximum and minimum principle states that absolute extreme values occur either at critical points found from the first derivative or at the endpoints of the interval.
- 📘 A four-step process is used to find absolute extrema: find the first derivative, locate critical values within the interval, evaluate the function at critical points and endpoints, and identify the highest and lowest function values.
- 🤔 The first derivative test involves setting the derivative equal to zero to find critical points, which are potential locations for maxima or minima.
- 📊 When the first derivative is not zero, the second derivative test can be used to determine if a critical point is a maximum, minimum, or neither by analyzing the concavity of the function.
- 📐 Endpoints are always checked because they can represent absolute maximum or minimum values, even if they are not critical points.
- 👉 The actual maximum and minimum values are found by evaluating the function at critical points and endpoints and then selecting the highest and lowest y-values.
- 🧮 For real-world problems, the strategy is the same: identify the function representing the situation, find critical points and endpoints, evaluate the function at these points, and determine the maximum or minimum based on the context.
- ✅ It's important to consider the context of the problem, as some variables like the number of items produced may only have meaningful values at whole numbers.
Q & A
What is the main focus of the video?
-The video focuses on extending the concept of relative extreme values to find absolute maximum and minimum values of a function over a specified interval or its entire domain.
What are relative maximum and minimum values?
-Relative maximum and minimum values are the highest or lowest points of a function in relation to the points around them, also known as the peaks or valleys on the function's graph.
What is the difference between relative and absolute extreme values?
-Relative extreme values are the highest or lowest points within a certain neighborhood of the function, while absolute extreme values are the highest or lowest points over the entire domain or interval of the function.
How does the maximum and minimum principle help in finding absolute extreme values?
-The maximum and minimum principle states that the absolute extreme values of a continuous function on a closed interval either occur at critical points or at the endpoints of the interval.
What is a critical point in the context of the video?
-A critical point is a point on the graph of a function where the first derivative is either zero or undefined, which could potentially correspond to a local maximum, local minimum, or a saddle point.
How does the first derivative test work?
-The first derivative test involves finding the critical points by setting the first derivative equal to zero and solving for x. Then, the function is evaluated at these critical points and at the endpoints of the interval to determine the absolute maximum and minimum values.
What is the role of the second derivative test in finding extreme values?
-The second derivative test can be used to determine whether a critical point is a maximum, minimum, or neither by evaluating the sign of the second derivative at the critical point.
How can a graphing calculator assist in finding absolute maximum and minimum values?
-A graphing calculator can be used to evaluate the function at critical points and endpoints, find x-intercepts, and graph the function to visually identify potential maximum and minimum points, thus saving time and reducing computational errors.
What is the significance of checking endpoints when finding absolute extreme values?
-Endpoints are significant because the absolute maximum or minimum value could occur at the endpoints of the interval, especially if the interval is not the entire domain of the function.
How does the video demonstrate the application of finding absolute extreme values in real-world problems?
-The video provides examples such as finding the maximum percentage of unemployed workers in service occupations over a certain period and maximizing the weekly profit from the production and sale of amplifiers, showing how these mathematical concepts can be applied to real-world scenarios.
What is the importance of understanding the context when applying the concept of maximization and minimization in real-world problems?
-Understanding the context is crucial because it determines the range of x-values to consider (such as only non-negative or whole number values), and it helps in interpreting the results in a way that makes sense for the specific problem at hand.
Outlines
📈 Introduction to Absolute Maximum and Minimum Values
This paragraph introduces the concept of absolute maximum and minimum values in the context of calculus. It explains the difference between relative extrema (local maxima or minima) and absolute extrema over a function's entire domain. The video aims to show how to use the first and second derivative tests to find these absolute values, which may occur at critical points or at the endpoints of a function's interval.
🔍 Applying the Maximum and Minimum Principle
The second paragraph delves into the maximum and minimum principle, which states that absolute extreme values of a continuous function on a closed interval occur either at critical points or at the endpoints of the interval. The process involves finding the first derivative, determining critical values within the interval, evaluating the function at these points and the endpoints, and then identifying the highest and lowest function values as the absolute maximum and minimum, respectively.
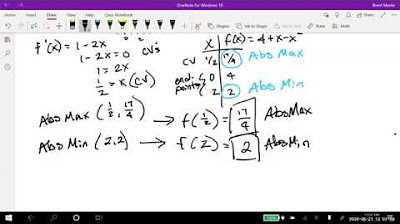
🧮 Example: Finding Absolute Extremes of a Function
This paragraph presents an example of finding the absolute maximum and minimum values of a function f(x) = x^4 - 2x^2 + 5 over the interval from x = -2 to x = 2. It outlines the steps of finding the first derivative, setting it to zero to find critical values, evaluating the function at these critical points and the endpoints, and then comparing the function values to determine the absolute maximum and minimum values and their locations.
📉 Evaluating Function Values at Critical Points and Endpoints
The fourth paragraph continues the example from the previous one, showing how to use a graphing calculator to evaluate the function at critical points and endpoints. It discusses finding the y-values associated with these x-values and identifying the highest and lowest y-values as the absolute maximum and minimum, respectively. The paragraph also notes the possibility of a minimum value occurring at more than one x-location.
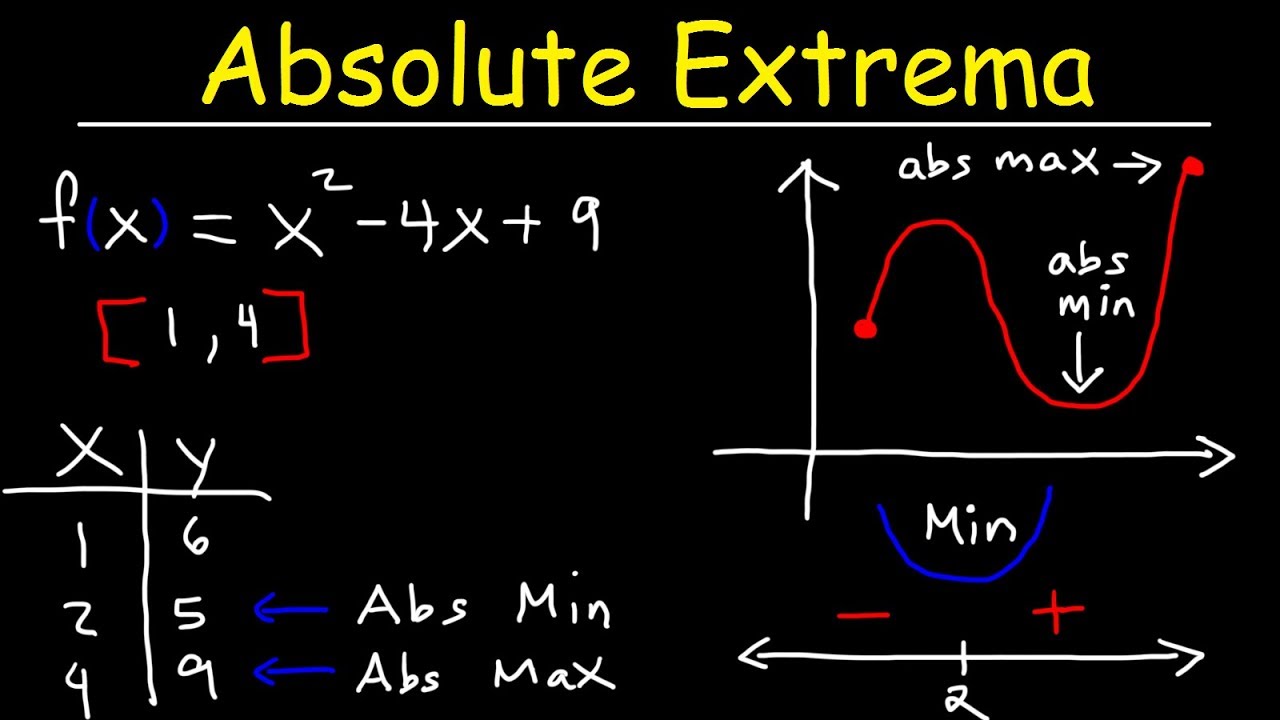
🔢 Examining Different Intervals for Absolute Extremes
This paragraph explores the concept of finding absolute maximum and minimum values over different intervals. It uses the function f(x) = x^3 - 3x + 2 and examines two intervals: from x = -2 to x = 3.5 and from x = -3 to x = -1.5. The paragraph explains that different intervals may have different absolute extreme values and emphasizes checking endpoints and critical points within each interval.
📚 Applying Calculus to Real-World Problems
The sixth paragraph shifts the focus to applying the concept of maximization and minimization to real-world problems. It provides an example of a function representing the percentage of unemployed workers in service occupations and shows how to find the year within a given period when the percentage was at its maximum using the previously discussed strategies.
🛒 Profit Maximization in a Production Context
The seventh paragraph discusses an example related to an electronic store's weekly profit from the production and sale of amplifiers. It outlines the process of finding the number of amplifiers that yield the maximum weekly profit. The paragraph covers taking the derivative of the profit function, finding critical values, and evaluating the function at these points and at the endpoints of a relevant interval to determine the maximum profit and the number of amplifiers associated with it.
📉 Endpoints and Critical Points in Real-World Applications
The eighth paragraph emphasizes the importance of considering both endpoints and critical points when finding maxima and minima, especially in real-world applications. It reiterates that without given endpoints, one must consider the context to determine the interval over which to search for extreme values, and it highlights that in some cases, only whole number values of x may be meaningful.
💰 Maximizing Profit with a Given Function
The final paragraph wraps up the discussion on using calculus to solve real-world problems, particularly focusing on maximizing profit. It reinforces the strategy of finding critical values, evaluating the function at these points and any relevant endpoints, and determining the highest value as the maximum profit. The paragraph also touches on the practicality of x values, noting that in some contexts, only whole numbers are applicable.
Mindmap
Keywords
💡Derivative Tests
💡Absolute Maximum and Minimum Values
💡Critical Values
💡First Derivative Test
💡Second Derivative Test
💡Maximum and Minimum Principle
💡Continuous Function
💡Relative Extreme Values
💡Endpoint Values
💡Quadratic Formula
💡Real-world Application
Highlights
The video discusses the concept of absolute maximum and minimum values, extending the understanding of relative maximum and minimum values.
Absolute maximum and minimum values are the highest and lowest points on the entire graph of a function, not just in relation to surrounding points.
Derivative tests are used to find relative maximum and minimum values, which are points of peak or valley on a function's graph.
The absolute maximum or minimum may occur at critical points or at the endpoints of the interval being considered.
The maximum and minimum principle states that absolute extreme values must occur at critical points or endpoints for a continuous function over an interval.
A four-step process is outlined to find absolute maximum and minimum values using the first derivative test and evaluating the function at critical points and endpoints.
The video provides a detailed example of finding absolute maximum and minimum values for a function over a specified interval.
The use of a graphing calculator is suggested as a time-saving tool for evaluating the function at various x values.
The concept is applied to real-world problems, such as finding the maximum unemployment percentage in a given period.
The method for solving for absolute maxima and minima is demonstrated with a function representing weekly profit from selling amplifiers.
The importance of considering the context of the problem is emphasized, as it affects the selection of appropriate x values for evaluation.
The video illustrates how to determine the number of amplifiers that yield the maximum profit using the first derivative test.
The process of finding the maximum or minimum value involves checking critical points and endpoints, and then evaluating the function at these points.
The video emphasizes that the maximum or minimum value can occur at endpoints, not just at critical points within the interval.
The application of the maximum and minimum principle is shown in a step-by-step approach for a function representing profit over a range of product quantities.
The transcript highlights the use of the first and second derivative tests in conjunction with the maximum and minimum principle to find absolute extreme values.
The video concludes with a summary of how to apply the concepts of maximization and minimization to solve real-world problems using derivative tests.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: