Calculus Chapter 2 Lecture 14 Optimization

Penn Online Learning

23 Jun 201616:19

EducationalLearning

32 Likes 10 Comments

TLDRIn this calculus lecture, Professor Greist delves into optimization, a practical application of derivatives for finding maxima and minima in various real-world scenarios. He explains the concept of critical points where the derivative is zero, and how the second derivative test can classify these points as local maxima, minima, or neither. The lecture includes examples, such as maximizing the volume of an open-topped box and minimizing a function with constraints, emphasizing the importance of checking endpoints for global extrema. The professor also introduces the idea of using Taylor expansion as an alternative to specialized tests for analyzing critical points.

Takeaways

📚 Optimization is a broad application of derivatives used to find the best solutions to problems like maximizing profit or minimizing drag on an airplane wing.
🔍 To find the maximum or minimum value of a function, one must first identify critical points, which are points where the derivative is zero or undefined.
📉 At a critical point, if the derivative is non-zero, it indicates that the function is either increasing or decreasing, not at a maximum or minimum.
📈 The second derivative test is a useful tool for classifying critical points: a positive second derivative indicates a local minimum, a negative one indicates a local maximum, and zero or undefined indicates inconclusive results.
🔧 The reason the second derivative test works is related to Taylor series expansion, where the leading term after the first derivative (which is zero at a critical point) determines the concavity of the function's graph.
📝 The Taylor expansion of a function at a critical point reveals that the function's graph locally resembles a parabola, with the sign of the second derivative indicating whether it opens upwards (minimum) or downwards (maximum).
📦 In optimization problems with constraints, such as maximizing the volume of an open-topped box by cutting corners from a square piece of material, one must consider the relationship between the variable and the constraints.
📈 When solving optimization problems, it's important to differentiate the function with respect to the variable, set the derivative equal to zero to find critical points, and then classify these points using the second derivative test.
🌐 For problems with constraints, one must also consider the endpoints of the domain as potential critical points, as they can represent global maxima or minima.
🌟 The global maximum or minimum of a function may not be at the critical points found by differentiation; it could be at the boundaries of the domain or even at infinity.
🔬 The process of optimization involves a combination of calculus techniques, including differentiation, second derivative testing, and understanding the behavior of functions at boundaries and infinity.

Q & A

What is the main topic of Professor Greist's lecture 14?
-The main topic of the lecture is optimization, which is an application of derivatives to find maxima and minima in various problems.
What are some real-world examples of optimization problems mentioned in the lecture?
-Examples include maximizing profit, minimizing drag on an airplane wing, and finding the best route through a complex network.
According to the lecture, what is a critical point in the context of optimization?
-A critical point of a function is an input at which the derivative vanishes, which could be at a maximum, minimum, or neither, such as at an inflection point.
Why is the second derivative test useful in classifying critical points?
-The second derivative test is useful because it helps determine if a critical point is a minimum (if the second derivative is greater than zero) or a maximum (if it is less than zero).
What does the sign of the second derivative at a critical point indicate about the function's behavior at that point?
-The sign of the second derivative indicates whether the function has a local maximum or minimum. A positive second derivative suggests a local minimum, while a negative one indicates a local maximum.
Why does the Taylor expansion at a critical point help in understanding the function's behavior?
-The Taylor expansion at a critical point helps because it simplifies the function to a quadratic form, showing the local behavior as if it were a parabola, which can indicate whether the point is a local maximum or minimum based on the sign of the leading coefficient.
In the example of maximizing the volume of an open-topped box, what is the significance of the critical points found?
-The critical points found in the example are potential candidates for the maximum volume. By evaluating the second derivative at these points, we can determine whether they correspond to maxima, minima, or neither.
What is the formula for the volume of the open-topped box in terms of the variable x and constant L?
-The volume of the open-topped box is given by the formula V = x * (L - 2x)^2, where x is the length of the side removed from the corners and L is the original side length of the square.
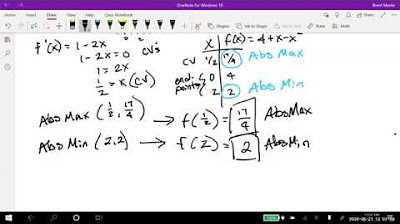
In the script, how is the global maximum of the function f(x) = x^3/3 - 3x^2 + 8x - 2 determined?
-The global maximum is determined by checking the values of the function at the critical points and the domain endpoints. In this case, the global maximum occurs at the right-hand endpoint, which is infinity, where the function tends towards infinity.
What is the importance of checking the endpoints of the domain when finding the global maximum or minimum of a function?
-Checking the endpoints is important because the global maximum or minimum may occur at these points, especially when the function is unbounded or the derivative does not exist there.

Outlines

00:00

📚 Introduction to Optimization with Calculus

Professor Greist introduces the topic of optimization, a key application of derivatives, which is used to find maxima and minima in various practical scenarios. The lecture explains how derivatives can be used to determine whether a function is increasing or decreasing at a given point, and how setting the derivative to zero can help identify critical points, which are potential maxima or minima. The concept of the second derivative test is also introduced, which helps classify critical points as either maxima, minima, or neither. The importance of considering the endpoints of a domain when seeking global extrema is highlighted.

05:03

🔍 Deep Dive into the Second Derivative Test and Taylor Expansion

This section delves deeper into the second derivative test, explaining its rationale through Taylor expansion around a critical point. The lecture illustrates how the sign of the second derivative can indicate whether a function has a local maximum or minimum at a critical point. An example involving sine squared times the logarithm of cosine is used to demonstrate the application of Taylor expansion to determine the nature of a critical point without relying on the second derivative test.

10:05

📏 Practical Application: Maximizing Volume of an Open-Topped Box

The script presents a practical problem of maximizing the volume of an open-topped box made by cutting corners from a square piece of material. The process involves setting up the volume as a function of the side length of the removed squares, differentiating with respect to this variable, and solving for critical points. The second derivative test is then used to determine that one of the critical points corresponds to a local maximum volume. The maximum volume is calculated by substituting the value of the critical point back into the volume function.

15:07

🌐 Exploring Global Extrema with Constrained Optimization

The final paragraph discusses the concept of global maxima and minima in the context of constrained optimization. An example function is given with a constraint that the variable must be non-negative. The derivative is computed, and critical points are found and classified using the second derivative test. The importance of checking the endpoints of the domain, including the behavior at infinity, is emphasized to ensure that the true global extrema are identified. The lecture concludes with a reminder to always verify the endpoints when seeking global extrema.

Mindmap

Keywords

💡Optimization

Optimization refers to the process of making a decision that maximizes or minimizes a particular metric, such as profit or cost. In the context of the video, it is the application of calculus to find the best possible outcome in various scenarios. For example, the video discusses how to maximize profit or minimize drag on an airplane wing using derivatives.

💡Derivatives

Derivatives in calculus represent the rate at which a quantity changes with respect to another quantity. They are used in the video to find the points where a function increases or decreases, which are crucial for identifying maxima and minima. The script mentions using derivatives to compute these points for optimization problems.

💡Maxima and Minima

Maxima and minima are the highest and lowest points of a function, respectively. The video's theme revolves around using derivatives to find these points, which are essential in optimization problems. The script provides examples of how to determine if a point is a maximum or minimum by analyzing the derivative at that point.

💡Critical Point

A critical point is a point on the graph of a function where the derivative is zero or undefined. The video explains that critical points are potential candidates for maxima, minima, or points of inflection. The script uses the concept of critical points to identify where to look for optima in functions.

💡Second Derivative Test

The second derivative test is a method used to determine whether a critical point is a maximum, minimum, or neither. If the second derivative at a point is positive, the point is a local minimum; if negative, it's a local maximum. The video script uses this test to classify critical points in the context of optimization.

💡Taylor Series

A Taylor series is a mathematical representation of a function as an infinite sum of terms, which are calculated from the values of the function's derivatives at a single point. The video script mentions Taylor series to explain why the second derivative test works, by showing how the function behaves locally around a critical point.

💡L'Hôpital's Rule

L'Hôpital's rule is a technique in calculus for evaluating limits of indeterminate forms. While not directly discussed in the script, it is mentioned in the context of the second derivative test, which shares a conceptual basis with L'Hôpital's rule in terms of understanding the behavior of functions.

💡Local vs. Global Extrema

Local extrema are the highest or lowest points in the vicinity of a certain point on a function's graph, whereas global extrema are the highest or lowest points on the entire graph. The video distinguishes between these by checking the endpoints of the domain in addition to critical points to find the global maximum or minimum.

💡Constraints

Constraints in optimization problems are limitations or conditions that must be met. The script gives an example where the optimization of a function is subject to the constraint that the variable must be greater than or equal to zero.

💡Differential

Although not deeply explored in the provided script, the concept of a differential is mentioned as a subtly different idea from the derivative. It is a measure of how a function changes with respect to changes in its input variable, which is a fundamental concept in calculus and will be discussed in the next lecture.

💡Volume Maximization

Volume maximization is a specific type of optimization problem discussed in the script, where the goal is to find the dimensions that will give the largest possible volume for a certain shape, such as an open-topped box formed by cutting corners from a square piece of material.

Highlights

Introduction to optimization, a key application of derivatives, for solving max-min problems.

Optimization theory's relevance to real-world problems such as maximizing profit and minimizing drag on airplane wings.

The definition of a critical point as an input where the derivative of a function vanishes.

Differentiation between critical points, maxima, minima, and inflection points.

The importance of considering points where the function is discontinuous or not differentiable in optimization problems.

The second derivative test for classifying critical points into local minima, maxima, or neither.

The intuition behind the second derivative test, relating to the shape of the graph near a critical point.

Use of Taylor series to understand why the second derivative test works.

An example of finding a local maximum for the function sine squared(x) times log(cosine(x)) at x=0.

Taylor expansion as an alternative to the second derivative test for analyzing critical points.

A practical example of maximizing the volume of an open-topped box made from a square sheet by cutting corners.

Differentiation of the volume function with respect to the size of the cut corners to find critical points.

The conclusion that the volume is maximized when the cut size is one-sixth of the side length of the square sheet.

An example of minimizing the function f(x) = x^3/3 - 3x^2 + 8x - 2 with the constraint x ≥ 0.

Finding global extrema by checking endpoints of the domain in addition to local extrema.

The concept that the global maximum or minimum may occur at the endpoints of the domain or at infinity.

The upcoming lecture's focus on the transition from the concrete notion of a derivative to the idea of a differential.

Transcripts

Browse More Related Video

3.1 - Using First Derivatives to Classify Max and Min Values

Math 11 - Section 3.4

Second Derivative Test Multivariable (Calculus 3)

Ex: Optimizing the Volume of a Box With Fixed Surface Area

Math1325 Lecture 10 1 - Relative Max & Min

AP Calculus AB and BC Unit 5 Review [Analytical Applications of Differentiation]