Finding Absolute Extrema

Sun Surfer Math
3 Mar 202212:51
EducationalLearning
32 Likes 10 Comments

TLDRThis video script is the third in a series focusing on critical values and extrema in calculus. It builds upon the first two lectures by introducing absolute extrema, which are the highest and lowest points on a graph, not just relative to a local area but across the entire domain. The lecturer explains that absolute extrema can occur at critical points or endpoints of a function's domain. Using examples, the script illustrates how to find absolute extrema by evaluating the function at critical points and endpoints, and then identifying the highest and lowest function values. The process is demonstrated with two functions, x^2 - 2x over the interval [0, 4] and x^3 - 12x over the interval [-4, 4], showing that absolute extrema can coincide with relative extrema but are not always the same. The script provides a clear method for finding absolute extrema, emphasizing the importance of considering both critical points and endpoints in the analysis.

Takeaways
  • 📌 **Critical Values Defined**: In the first video, the concept of critical values was introduced as points on a graph where the derivative is zero or undefined.
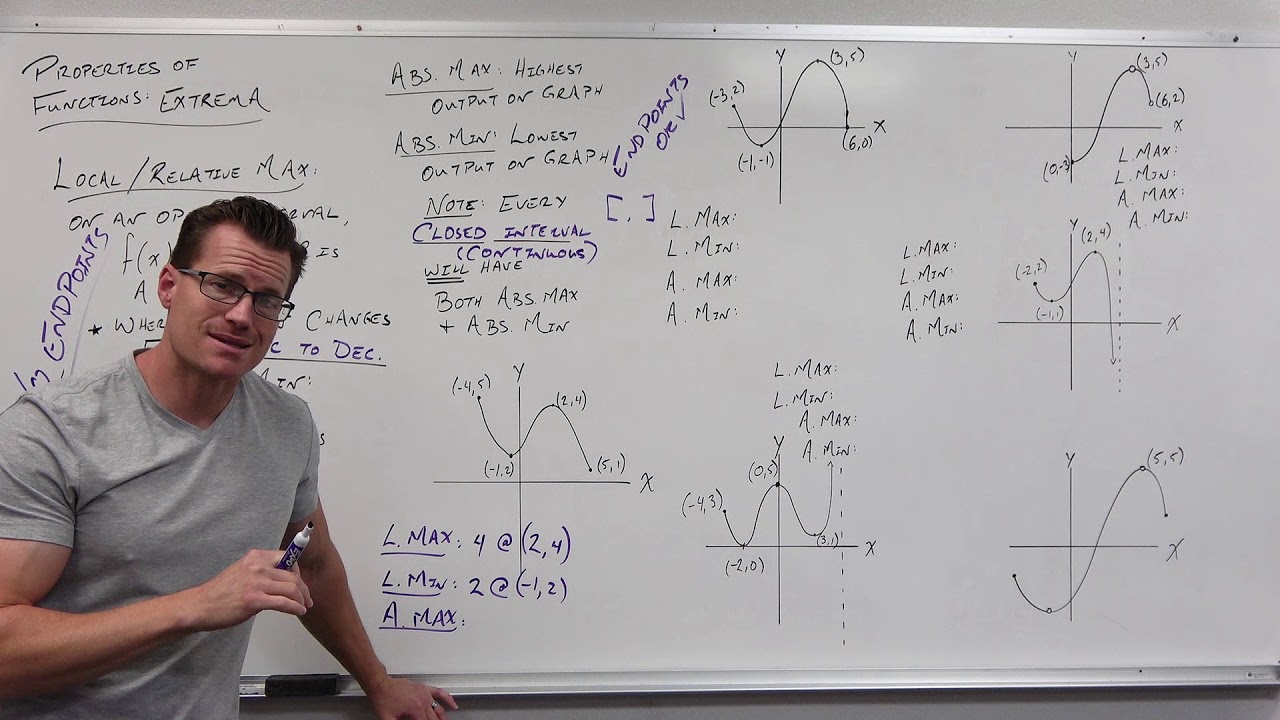
  • 📈 **Relative Extrema**: The second video discussed relative extrema, which are the highest or lowest points within a certain area of a graph.
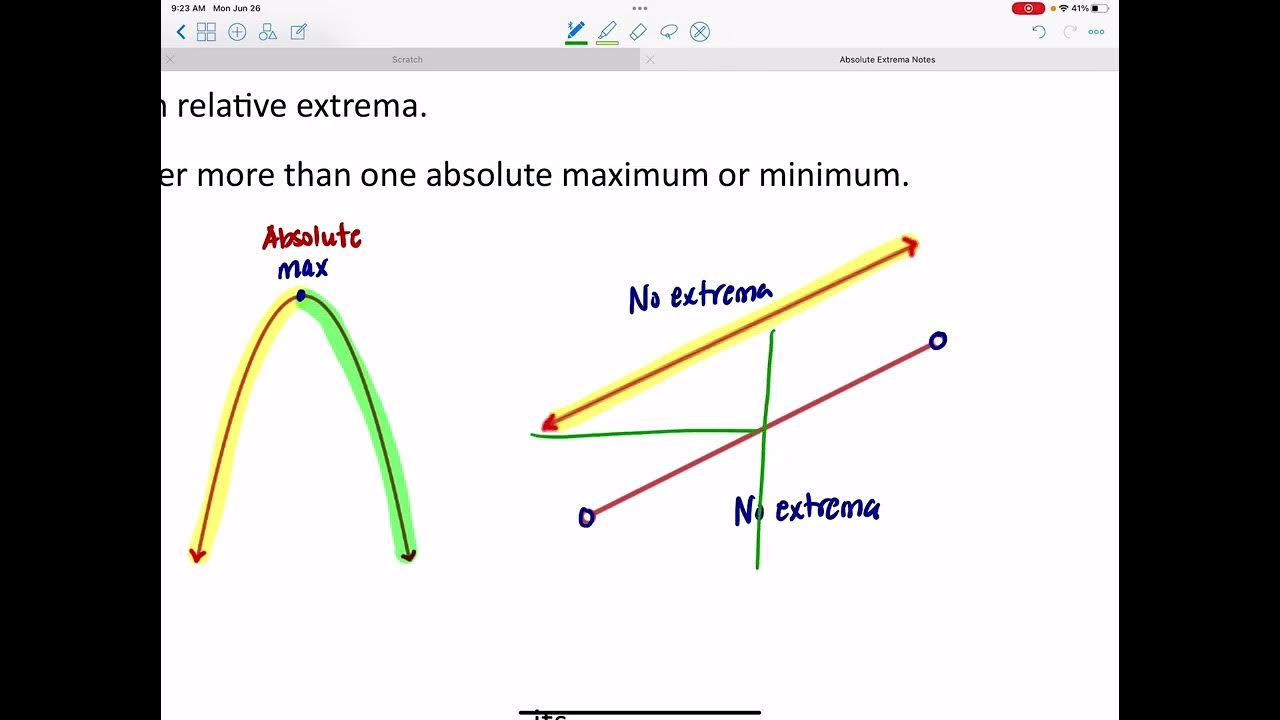
  • 🔍 **Absolute Extrema**: This video focuses on absolute extrema, which are the highest or lowest points on the entire graph, not just within a local area.
  • 🔢 **Identifying Absolute Extrema**: Absolute extrema can occur at critical points or endpoints of the graph's domain.
  • 🏁 **Endpoints Consideration**: Endpoints are always considered when searching for absolute extrema, even if they are not relative extrema.
  • 🔄 **Example Analysis**: The video provided examples to illustrate the concepts, showing how relative extrema can also be absolute extrema.
  • ∞ **Infinite Endpoints**: If a graph extends to infinity at an endpoint, there is no absolute extremum at that point, as values can get infinitely large or small.
  • 🔑 **Derivative Role**: Finding the derivative of the function is crucial for determining critical values, which are potential locations for relative or absolute extrema.
  • 📊 **Table of Values**: A table of values is used to compare function values at endpoints and critical points to identify absolute extrema.
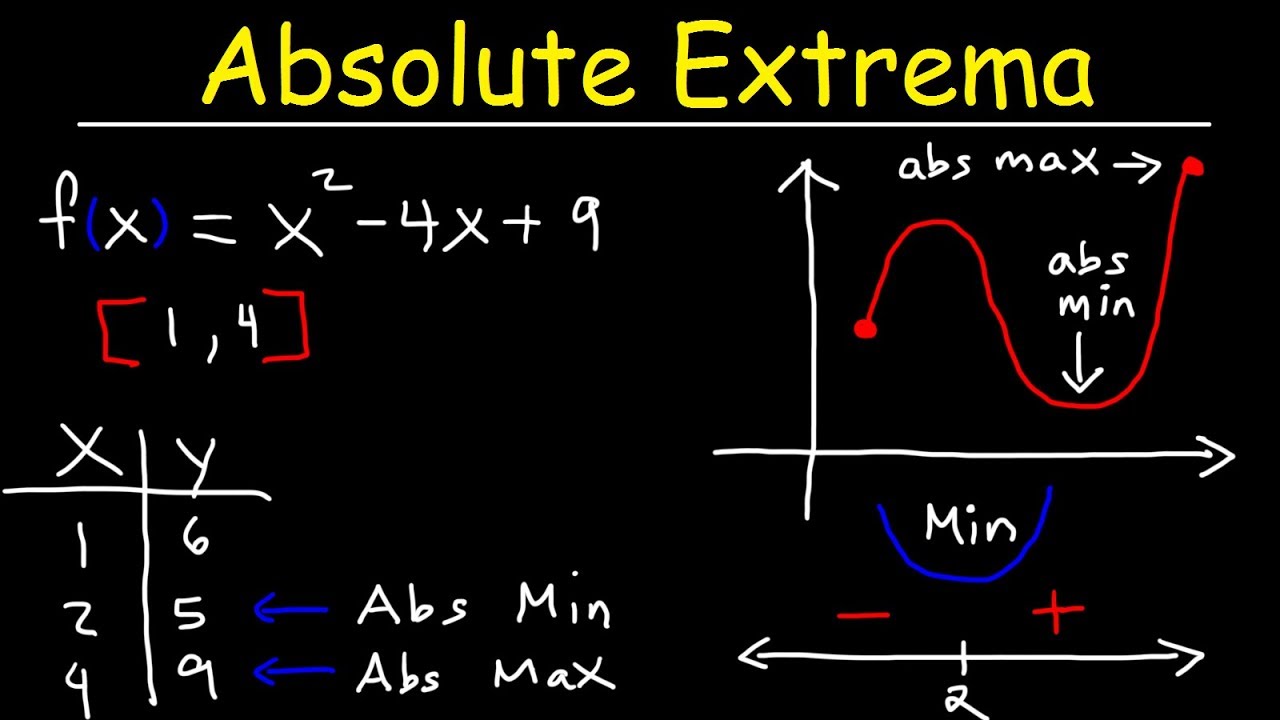
  • 🔺 **Absolute Maximum Example**: The function (x^2 - 2x) over the interval [0, 4] was used to demonstrate finding absolute extrema, with the absolute maximum at (x = 4) and the absolute minimum at (x = 1).
  • 🔻 **Absolute Minimum Example**: For the function (x^3 - 12x) over the interval [-4, 4], the absolute maximum was found at both (x = -2) and (x = 2), and the absolute minimum at (x = -4) and (x = 4).
Q & A

  • What is a critical value in the context of calculus?

    -A critical value is a value of the variable at which the derivative of a function is either zero or undefined. These points are considered as potential locations for relative or absolute extrema.

  • What are the differences between relative extrema and absolute extrema?

    -Relative extrema are the highest or lowest points within a certain area of a graph, whereas absolute extrema are the highest or lowest points on the entire graph, regardless of the area.

  • How do you find the critical values of a function?

    -To find the critical values, you first find the derivative of the function. Then, you set the derivative equal to zero and solve for the variable to find the critical points.

  • What are the possible locations for absolute extrema on a graph?

    -Absolute extrema, if they exist, can occur at critical points or at endpoints of the graph's domain.

  • How do you determine if a point is an absolute extremum?

    -You compare the function values at the critical points and endpoints. The highest value indicates the absolute maximum, and the lowest value indicates the absolute minimum.

  • What is the significance of the endpoints in finding absolute extrema?

    -Endpoints are the boundary values of the function's domain. They are considered when finding absolute extrema because the highest or lowest point on the graph can occur at these boundary points.

  • How does the process of finding absolute extrema differ from finding relative extrema?

    -Relative extrema are found solely at critical values, whereas absolute extrema can occur at critical values or endpoints, depending on the function and its domain.

  • What is the role of the derivative in finding extrema?

    -The derivative of a function gives the slope of the tangent line at a point on the graph. Setting the derivative equal to zero helps in finding points where the function changes from increasing to decreasing or vice versa, which are potential extrema.

  • In the given examples, how are the absolute extrema determined for the function x^2 - 2x over the interval [0, 4]?

    -The critical value is found by setting the derivative (2x - 2) equal to zero, which gives x = 1. The endpoints are x = 0 and x = 4. By evaluating the function at these points, the absolute extrema are determined as the highest and lowest function values.

  • For the function x^3 - 12x over the interval [-4, 4], how are the critical values determined?

    -The derivative is 3x^2 - 12, which is set to zero to find critical points. Solving gives x^2 = 4, so x = -2 and x = 2 are the critical values.

  • What is the relationship between the critical points and the absolute extrema in the second example with the function x^3 - 12x?

    -In the second example, the absolute maximum occurs at both a critical value (x = 2) and an endpoint (x = -4 and x = 4), while the absolute minimum occurs at a critical value (x = -2) and is also tied with the value at the endpoint (x = -4).

  • How does the process of creating a table of values help in finding the absolute extrema?

    -A table of values allows you to systematically compare the function's outputs at critical points and endpoints. By identifying the highest and lowest values in this table, you can determine the absolute maximum and minimum of the function on a given interval.

Outlines
00:00
📈 Understanding Critical Values and Absolute Extrema

This paragraph introduces the topic of absolute extrema, which are the highest or lowest points on a graph, contrasting them with relative extrema. The speaker explains that an absolute extremum can also be a relative extremum, using a graph as an example. The concept is further clarified with examples that include graphs with absolute maxima and minima, and the importance of considering both critical points and endpoints when identifying absolute extrema is emphasized.

05:02
🔍 Finding Absolute Extrema with Examples

The paragraph provides a step-by-step guide on how to find the absolute extrema of a function within a given interval. It starts by identifying critical values and endpoints, then uses a table to compare the function values at these points. The process is illustrated with two examples: the first involves finding the absolute extrema of x^2 - 2x over the interval [0, 4], and the second deals with x^3 - 12x over the interval [-4, 4]. The speaker demonstrates how to calculate the function values at critical points and endpoints and how to determine the absolute maximum and minimum from these values.

10:03
📊 Evaluating Function Values at Critical Points and Endpoints

This paragraph continues the process of finding absolute extrema by evaluating the function values at critical points and endpoints for the given examples. It shows the calculations for the function values at -4, -2, 2, and 4 for the second example. The results are then compared to identify the absolute maximum and minimum values. The speaker highlights that absolute extrema can occur at either critical values or endpoints, and the process concludes by identifying the points where the absolute maximum and minimum occur in the example.

Mindmap
Keywords
💡Critical Values
Critical values are points on the graph of a function where the derivative is either zero or undefined. They are crucial for identifying potential relative or absolute extrema of a function. In the video, critical values are used to find both relative and absolute extrema, which are the highest or lowest points on a graph.
💡Extrema
Extrema refers to the highest or lowest points on a graph of a function. These can be either relative or absolute. Relative extrema are the highest or lowest points within a certain area of the graph, while absolute extrema are the highest or lowest points on the entire graph. The video discusses how to find both types using critical values.
💡Absolute Extrema
Absolute extrema are the points on a graph that represent the highest or lowest values the function can achieve over its entire domain. Unlike relative extrema, which are local, absolute extrema are global in nature. The video explains that absolute extrema can occur at critical points or endpoints of the function's domain.
💡Relative Extrema
Relative extrema are points on a graph where the function's value is higher or lower than the values of the function in its immediate vicinity. These points are local maxima or minima and do not necessarily represent the highest or lowest values on the entire graph. The video discusses how critical values are used to identify relative extrema.
💡Derivative
The derivative of a function measures the rate of change of the function's output with respect to its input. In the context of the video, finding the derivative of a function is the first step in identifying critical values, which are then used to find extrema. The video mentions setting the derivative equal to zero to find critical points.
💡Endpoints
Endpoints refer to the boundary points of the domain of a function. When finding absolute extrema, endpoints are considered because the highest or lowest value of the function can occur at these points. The video provides examples where the absolute extrema occur at endpoints of the function's domain.
💡Function Value
The function value at a given point is the value of the function's output for a specific input. In the context of finding extrema, the function value indicates the height of the graph at a particular x-value. The video uses function values to create a table of values to determine the absolute extrema.
💡Table of Values
A table of values is a method used to organize and compare the function values at various points, including critical points and endpoints. In the video, a table of values is created to systematically evaluate the function at different x-values and identify the absolute extrema.
💡Infinity
In the context of the video, infinity refers to the unbounded nature of certain functions, such as those with vertical asymptotes. The video mentions that if a graph has arrows indicating that it goes down to negative infinity, there is no absolute minimum because the function value can become arbitrarily low.
💡Example
Examples in the video are used to illustrate the process of finding absolute and relative extrema. They provide practical demonstrations of how to apply mathematical concepts to specific functions. The video includes examples with functions like x squared minus 2x and x cubed minus 12x to show how to calculate and interpret extrema.
💡Interval
An interval is a set of numbers within a certain range, and it defines the domain over which extrema are sought. In the video, the interval from 0 to 4 is used as the domain for finding the absolute extrema of the given function. The interval helps to limit the scope of the analysis to a specific range of the function.
Highlights

The lecture discusses the concept of absolute extrema, which are the highest or lowest points on a graph.

Absolute extrema can be found using critical values, which were defined in the first video.

The video explains the difference between relative and absolute extrema, noting that a point can be both.

Examples are provided to illustrate how absolute extrema can occur at critical points or endpoints of a graph.

The video demonstrates that absolute extrema do not necessarily coincide with relative extrema.

A method to find absolute extrema is presented, which involves evaluating function values at endpoints and critical points.

The importance of considering both endpoints and critical points when searching for absolute extrema is emphasized.

An example is given to show how to find the absolute extrema of a function over a specified interval.

The process of finding critical values by setting the derivative of the function to zero is explained.

The concept of creating a table of values to compare function values at endpoints and critical points is introduced.

It is shown that the absolute extrema will be the highest or lowest function values from the table of values.

The video provides a step-by-step guide to finding the absolute extrema for the function x^2 - 2x on the interval [0, 4].

Another example demonstrates finding the absolute extrema for the function x^3 - 12x on the interval [-4, 4].

The video concludes by summarizing the method for finding absolute extrema and its practical application in calculus.

The importance of evaluating function values at critical points and endpoints to determine absolute extrema is reiterated.

The video highlights the mathematical process of finding absolute extrema, which is crucial for understanding calculus concepts.

The practical application of finding absolute extrema is shown through detailed examples, enhancing the viewer's understanding.

The lecture concludes by reinforcing the method's utility in calculus, particularly in optimization problems and analysis of functions.

Transcripts

Browse More Related Video

BusCalc 19 Local and Global Extrema

Absolute Extrema

Properties of Functions - Extrema (Precalculus - College Algebra 10)

Finding Absolute Maximum and Minimum Values - Absolute Extrema

How to recognize relative and absolute maxima and minima | Functions | Algebra I | Khan Academy

Relative and Absolute Maximums and Minimums | Part II

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Critical ValuesExtremaGraph AnalysisAbsolute MaximumAbsolute MinimumRelative MaximumRelative MinimumDerivativeMathematicsLecture SeriesEducational Content