Electric Flux and Gauss' Law - Review for AP Physics C: Electricity and Magnetism

The script begins with an introduction to electric flux and Gauss' law in the context of AP Physics C: Electricity and Magnetism. It explains that electric flux is a measure of the electric field passing through a defined area and is symbolized by uppercase Phi with a subscript E. The equation for electric flux through a uniform electric field is discussed, highlighting its similarity to the work equation in physics. The script also delves into the concept of a closed surface and its relevance to calculating net electric flux, using a right triangular box as an example to illustrate the process.

This paragraph explores the calculation of electric flux through different surfaces of a right triangular box, considering the angle between the electric field and the area vector. It explains that the electric flux is negative when the electric field is entering a closed surface and positive when it is exiting. The discussion includes the flux through the rectangular sides, triangular sides, and the top surface of the box, leading to the conclusion that the net electric flux through the closed surface sums up to zero.

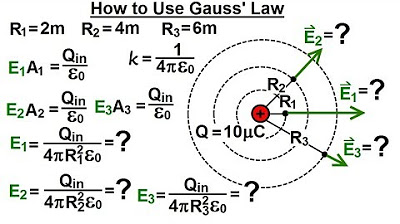
The script moves on to apply Gauss' law to calculate the electric flux through a sphere concentric with a point charge. It clarifies that the electric field around a point charge is not uniform, necessitating an integral approach. The electric field is constant at a constant radius, allowing for simplification using Coulomb's law. The final result demonstrates that the electric flux through the sphere is equal to the charge of the point charge divided by the permittivity of free space, regardless of the sphere's radius, showcasing Gauss' law in action.

This section delves deeper into the specifics of using Gauss' law, emphasizing the selection of Gaussian surfaces that simplify calculations due to the electric field's alignment with the surface normals. The script discusses the independence of electric flux from the size of the Gaussian surface when the enclosed charge is constant. It also introduces the concept of charge densities and their application in solving for electric fields using Gauss' law, specifically for symmetric charge distributions.

The script presents an example of using Gauss' law to determine the electric field surrounding an infinitely large, thin plane of positive charges with uniform surface charge density. It explains the selection of an appropriate Gaussian surface—a cylinder with a horizontal axis—and the rationale behind it. The calculation leads to the conclusion that the electric field is uniform and independent of the distance from the plane, highlighting the principles of Gauss' law in symmetrical charge distributions.

Building on the previous example, this paragraph considers the scenario of adding an equal magnitude, parallel, infinite plane of negative charges to the positively charged plane. The script describes the resulting electric fields and their interactions, leading to the conclusion that the electric field outside the two parallel planes is zero, while the field between the planes doubles that of a single plane, reinforcing the concept of superposition in electric fields.

The final paragraph reviews the concept that outside a uniformly charged sphere, the electric field behaves as if the sphere were a point charge. The script uses Gauss' law to prove this by comparing the electric field at a distance from a charged sphere to that of a point charge, showing that the electric field diminishes with the square of the distance from the center, regardless of the sphere's size, thus concluding the review of electric flux and Gauss' law.