Magnetic Fields, Flux Density & Motor Effect - GCSE & A-level Physics (full version)
TLDRThis script delves into the principles of magnetism, explaining the concept of magnetic field lines, their directionality from north to south poles, and how they form closed loops within a magnet. It explores the interaction between magnets and the resulting attraction or repulsion, highlighting the density of field lines and the force they exert. The script also covers the relationship between magnetism and electricity, introducing the motor effect and Fleming's left-hand rule for predicting the force on a current-carrying wire in a magnetic field. It concludes with practical methods to measure magnetic flux density, either directly or graphically, providing a comprehensive understanding of fundamental magnetic principles.
Takeaways
- 🧲 The concept of magnetic field lines, which are invisible lines that represent the direction and strength of a magnetic field, is introduced.
- 🗺️ Magnetic field lines always originate from the North Pole and terminate at the South Pole, forming closed loops without breaking or crossing.
- 🔍 When two magnets are aligned with their like poles facing each other, the magnetic field lines become denser, indicating a stronger force that repels the magnets.
- 📍 The terms 'North Pole' and 'South Pole' are derived from the way materials align with Earth's magnetic field, pointing towards the Earth's respective poles.
- 🌐 The Earth itself acts as a giant magnet, with its magnetic North Pole actually being geographically in the South, which can be counterintuitive.
- 📊 Flux, represented by the Greek letter Phi (Φ), measures the total magnetic field lines passing through a given area, with the unit Weber (Wb).
- 📉 Flux density, symbolized by B and measured in Tesla (T), is the concentration of magnetic field lines per unit area, indicating the strength of the magnetic field.
- 🔌 The interaction between electricity and magnetism is demonstrated by the magnetic field created around a wire carrying an electric current.
- ✋ Maxwell's right-hand rule and Fleming's left-hand rule are used to determine the direction of magnetic field lines and the force on a current-carrying conductor in a magnetic field, respectively.
- 🔢 The magnitude of the force experienced by a current-carrying wire in a magnetic field is calculated using the formula F = BIL, where F is force, B is magnetic flux density, I is current, and L is the length of the wire.
- 📈 The magnetic flux density can be experimentally determined by measuring the force on a wire using a balance, or graphically by plotting mass change against current and calculating the gradient.
Q & A
What are magnetic field lines and how do they relate to the force on a tiny North Pole?
-Magnetic field lines are imaginary lines that represent the direction and strength of a magnetic field. They show the force on or the direction that a tiny North Pole would take, with the lines always going from the North Pole to the South Pole of a magnet.
Why do magnetic field lines never break or cross?
-Magnetic field lines never break or cross because they represent a continuous loop of magnetic force. Inside a magnet, these lines continue and form a complete loop, ensuring the magnetic field's continuity.
What happens when two magnets are aligned with their like poles facing each other?
-When two magnets have their like poles facing each other, such as north-north, the magnetic field lines become more compact in the middle due to the repulsion between the poles. This results in a greater force trying to push the magnets apart.
How are the terms 'North Pole' and 'South Pole' of a magnet derived?
-The terms 'North Pole' and 'South Pole' come from the observation that certain materials align themselves with the Earth's magnetic poles. The end pointing towards the Earth's North Pole is called the North Pole, and the opposite end is the South Pole.
What is the difference between the Earth's geographical poles and its magnetic poles?
-The Earth's geographical North Pole is actually the magnetic South Pole, and vice versa. This is because the Earth acts as a giant magnet, and like poles repel each other, so the field lines go from the Earth's Antarctic to the Arctic.
What is meant by the term 'flux' in the context of magnetism?
-In magnetism, 'flux' (represented by the Greek letter Phi, Φ) refers to the total amount of magnetism passing through a given area, analogous to the amount of field lines passing through that area.
What is the relationship between magnetic flux and flux density?
-Flux density (represented by the symbol B) is the measure of how tightly packed the magnetic field lines are, or how much magnetism is passing through a unit area. Flux is related to flux density by the equation Flux = B * Area.
How is the direction of the magnetic field around a current-carrying wire determined?
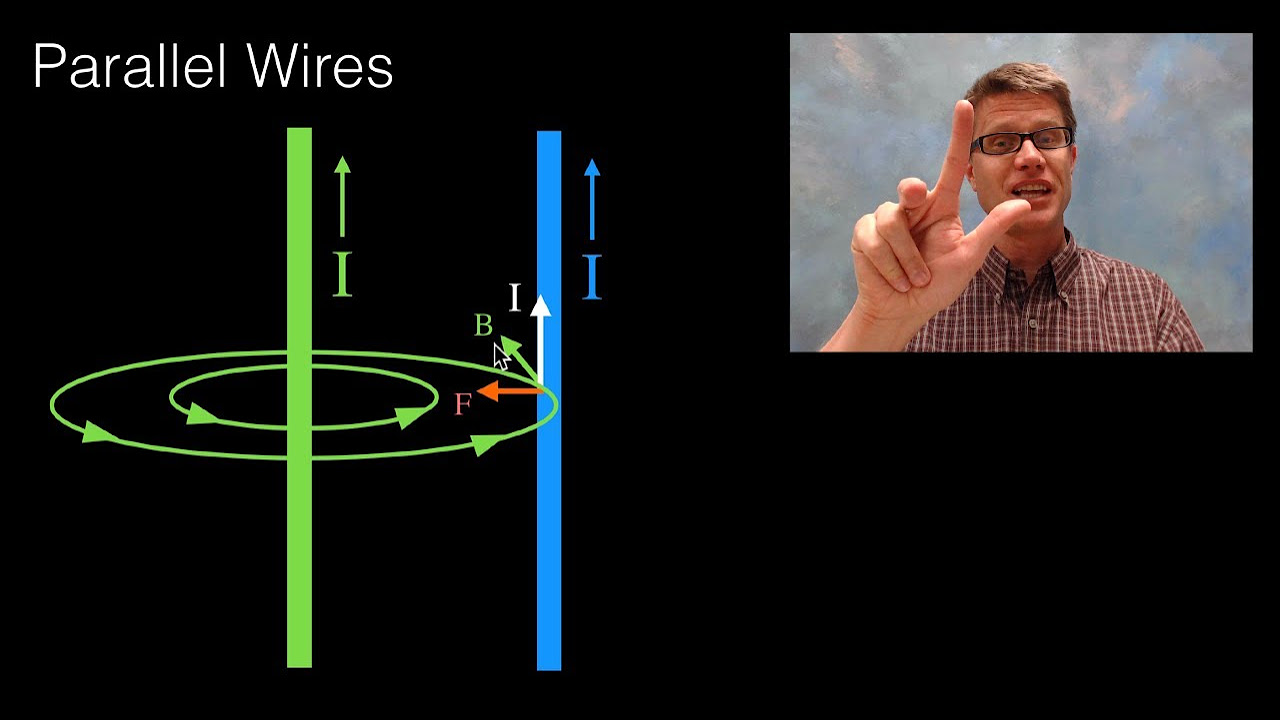
-The direction of the magnetic field around a current-carrying wire is determined using the right-hand rule or the corkscrew rule, where if you point your thumb in the direction of the current, your fingers will curl around the wire in the direction of the magnetic field lines.
What is the motor effect, and how does it relate to Fleming's left-hand rule?
-The motor effect is the movement of a current-carrying wire in a magnetic field due to the force exerted on it. Fleming's left-hand rule helps predict the direction of this force and the resulting movement of the wire, based on the direction of the magnetic field and the current.
How can the magnitude of the force on a current-carrying wire in a magnetic field be calculated?
-The magnitude of the force on a current-carrying wire in a magnetic field can be calculated using the formula F = B * I * L, where F is the force, B is the magnetic flux density, I is the current, and L is the length of the wire.
What is a method to measure the magnetic flux density using a top-pan balance and a current-carrying wire?
-By placing a current-carrying wire between two magnets and measuring the force exerted on the wire using a top-pan balance, one can calculate the magnetic flux density using the formula B = (mg / (I * L)), where mg is the measured mass on the balance, I is the current, and L is the length of the wire.
Outlines
🧲 Understanding Magnetic Fields and Pole Interaction
This paragraph introduces the concept of magnetic fields, which are invisible lines that represent the force direction a North Pole would take. It explains how objects like iron filings align with these fields and how field lines always form complete loops, exiting a magnet's North Pole and reentering its South Pole. The script discusses how magnets with like poles repel each other, creating dense field lines that increase the force between them. It also clarifies the naming of magnetic poles based on Earth's poles and the peculiarity of Earth's magnetic field, which has its North Pole near the geographic South Pole. The paragraph concludes with an explanation of magnetic flux, the total number of field lines passing through an area, and its density, symbolized by B and measured in Tesla.
🔗 Linking Magnetism, Electricity, and Flux Density
The second paragraph delves into the relationship between magnetism and electricity, describing how a current-carrying wire generates a magnetic field around it. It introduces Maxwell's right-hand rule for determining the direction of the magnetic field around a wire and explains the motor effect, where a current-carrying wire in a magnetic field experiences a force. Fleming's left-hand rule is used to predict the direction of this force. The paragraph also covers the formula for calculating the force on a wire in a magnetic field (F = BIL) and how flux density can be determined by rearranging this formula. It touches on the representation of three-dimensional magnetic fields on a two-dimensional plane using dots and crosses.
📏 Measuring Magnetic Flux Density Using a Current-Carrying Wire
This paragraph explains how to measure magnetic flux density by using a setup with two magnets and a wire carrying a current. It describes a method where the force exerted on the wire due to the magnetic field is balanced by the weight of the magnets, allowing for the calculation of magnetic flux density using the formula B = mg/(I * L). The paragraph also suggests a graphical method for determining flux density more accurately by plotting the change in mass against the change in current and using the gradient of the resulting line.
📚 Practical Application: Measuring Magnetic Flux Density
The final paragraph discusses a practical approach to measuring magnetic flux density, involving attaching magnets to a bracket and passing a current through a wire placed between them. It explains how to set up the experiment to measure the force on the wire using a top-pan balance and how to calculate the magnetic flux density from the measured mass change. The paragraph concludes with the formula for flux density and a reminder that the actual values obtained in experiments are typically in milliTeslas or microTeslas, much smaller than the example value calculated.
Mindmap
Keywords
💡Magnetic field lines
💡North and South Poles
💡Flux
💡Flux density (B)
💡Magnetism
💡Motor effect
💡Fleming's left-hand rule
💡Magnetic flux density
💡Right-hand rule
💡Free moving charge
Highlights
Magnetic field lines are invisible lines that show the direction of force on a tiny North Pole and are always unbroken loops.
Magnetic field lines originate from the North Pole and terminate at the South Pole, never crossing or breaking.
When two magnets are aligned in the same direction, their field lines connect, forming a single large magnetic field.
Opposing magnetic poles, such as North-North, create a dense concentration of field lines and a repulsive force.
The density of magnetic field lines correlates with the force experienced by objects within the field.
Magnetic flux, represented by the Greek letter Phi, measures the total magnetism passing through an area.
Flux density (B) is the concentration of magnetic field lines per unit area, measured in Tesla.
The Earth acts as a giant magnet with its magnetic North Pole actually being geographically south.
Fleming's left-hand rule is used to determine the direction of force on a current-carrying wire in a magnetic field.
The motor effect describes the movement of a wire within a magnetic field due to the interaction of magnetic fields.
The magnitude of force on a wire in a magnetic field can be calculated using the formula F = BIL.
Magnetic flux density can be graphically determined by plotting mass change against current and calculating the gradient.
Maxwell's right-hand rule helps determine the direction of magnetic field lines around a current-carrying wire.
The relationship between electricity and magnetism is fundamental, affecting each other's behavior.
A practical method to measure magnetic flux density involves using a top-pan balance and current-carrying wire between two magnets.
The direction of conventional current is opposite to the flow of electrons in a circuit.
Fleming's right-hand rule is an alternative to the left-hand rule, but is used in different contexts.
The force on a wire in a magnetic field is maximized when the wire and magnetic field are perpendicular to each other.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: