22. Quantum mechanics IV: Measurement theory, states of definite energy
TLDRThe transcript is a detailed lecture on quantum mechanics, focusing on the wave function and its relationship with the concept of time, as well as the quantization of energy and momentum. The professor begins by addressing a question about the absence of time in wave function equations, explaining that the wave function describes a state at a single instant in time, analogous to Newtonian mechanics where position and momentum fully describe a particle's state at any given moment. The lecture then delves into the probabilistic nature of quantum mechanics, where the wave function squared gives the probability density of finding a particle at a certain location. The professor further explores the measurement problem and the collapse of the wave function, emphasizing the difference between quantum and classical mechanics. The discussion also touches on the uncertainty principle and the mathematical underpinnings of quantum theory, particularly the role of linear algebra. Finally, the lecture explores the particle in a box model, illustrating how the wave function must be zero at the boundaries, leading to quantized energy levels and the characteristic wave-like solutions within the box. This model provides insight into the quantization of energy in quantum systems.
Takeaways
- 📌 The concept of time in quantum mechanics is not directly referenced in wave functions, which describe a state at a single instant in time.
- 🌊 The wave function ψ(x) contains complete knowledge of a particle's state, analogous to Newtonian mechanics where position and momentum fully describe a particle's state at an instant.
- 📏 In quantum mechanics, the probability density for finding a particle is given by the absolute square of the wave function ψ(x).
- 🚀 The momentum of a particle in a given state can be found by expressing the wave function as a sum of momentum eigenfunctions ψ_p(x) and finding the coefficients in this expansion.
- 🔍 The probability of measuring a particular momentum is given by the absolute square of the corresponding coefficient in the momentum eigenfunction expansion.
- ⏲️ The time evolution of the wave function ψ(x) is described by the Schrödinger equation, which provides the time-dependent behavior of the state.
- 🚨 The act of measurement in quantum mechanics causes the wave function to 'collapse' to a particular outcome, providing a definite result for the measured property.
- 🔄 The Heisenberg uncertainty principle is a mathematical consequence of the wave function description, where precise knowledge of position and momentum cannot coexist.
- 🧲 The energy of a quantum particle is not always just kinetic; it also includes potential energy when the particle is in a potential field.
- 📐 The Schrödinger equation for a particle in a one-dimensional box leads to quantized energy levels, which are integer multiples of a fundamental level, providing a clear example of energy quantization.
- 🔑 The solutions to the Schrödinger equation for a particle in a box are sines and cosines, which are normalized to zero at the boundaries, reflecting the physical condition that the particle cannot be found outside the box.
Q & A
What is the significance of the wave function ψ(x) in quantum mechanics?
-The wave function ψ(x) in quantum mechanics is a mathematical description of the quantum state of a particle. It contains all the information about the system, such as the probability distribution for the position of the particle, and can be used to calculate other properties like momentum.
Why is the concept of time not explicitly mentioned in the wave function?
-The wave function ψ(x) describes the state of a quantum system at a particular instant in time. Time evolution is considered separately, and the time-dependent Schrödinger equation is used to describe how the wave function changes over time.
What is the analogy used by the professor to explain the concept of a state in classical mechanics?
-The professor uses the analogy of Newtonian mechanics, where the state of a particle is completely given by its position (x) and momentum (p) at a particular instant. This pair of numbers is sufficient to predict the future behavior of the particle using Newton's laws.
How does the professor explain the probability of finding a particle in a certain location?
-The probability of finding a particle at a certain location is given by the absolute value squared of the wave function ψ(x) at that location, i.e., |ψ(x)|^2. This is known as the probability density.
What is the relationship between the wave function and momentum in quantum mechanics?
-The relationship between the wave function and momentum is more complex than with position. The professor explains that one must expand the given wave function ψ(x) in terms of functions ψ_p(x), which are associated with definite momentum states, and the probability of obtaining a certain momentum is given by the absolute square of the corresponding expansion coefficient.
What does the professor mean by the 'collapse of the wave function'?
-The collapse of the wave function refers to the process in quantum mechanics where the wave function changes abruptly after a measurement is made. For example, if the momentum of a particle is measured, the wave function collapses to a state associated with the measured momentum value.
How does the professor address the question about the normalization of the wave function?
-The professor explains that the wave function must be normalized so that the integral of the absolute value squared of ψ(x) over all space is equal to 1. This ensures that the total probability of finding the particle somewhere in space is 100%.
What is the Heisenberg Uncertainty Principle, and how does it relate to the discussion in the script?
-The Heisenberg Uncertainty Principle states that it is impossible to simultaneously know the exact position and momentum of a particle. The professor implies that this principle is a mathematical consequence of the wave function description, where measuring one quantity precisely affects the other.
What is the role of linear algebra in quantum mechanics?
-Linear algebra is fundamental to quantum mechanics as it provides the mathematical framework for handling the vector space of quantum states, the superposition principle, and the manipulation of state vectors and operators.
How does the professor describe the energy states of a particle in a one-dimensional box?
-The professor describes the energy states of a particle in a one-dimensional box as quantized, with the wave function being sinusoidal within the box and zero outside. The energy levels are given by \( E_n = \frac{\hbar^2 \pi^2}{2mL^2} n^2 \), where \( n \) is an integer, \( \hbar \) is the reduced Planck constant, \( m \) is the mass of the particle, and \( L \) is the length of the box.
What is the significance of the Schrödinger equation in the context of the script?
-The Schrödinger equation is the master formula that governs the behavior of quantum systems. It is used to find the allowed wave functions and energy levels of a particle in a given potential, which is a central concept discussed in the script.
Outlines
📧 Email Inquiry about Wave Function and Time
The professor begins by referencing an email from students, Jerry Wang and Emma Alexander, who question the absence of time in the wave function ψ(x) and its relation to time. The professor clarifies that the current discussion is limited to a single instant in time, analogous to Newtonian mechanics where the position and momentum at a single instant can predict future states. The wave function ψ(x) is a complete description of a quantum system at a moment, and the probability density for finding a particle is given by the square of the wave function's absolute value. The professor also discusses the relationship between the wave function and momentum, highlighting the complex nature of quantum mechanics.
📏 Quantum States and Momentum Measurement
The discussion shifts to the specifics of quantum states and the probability of measuring certain momentum values. The professor explains the mathematical representation of these probabilities using coefficients of functions ψ_p(x), which are related to the allowed values of momentum. The integral of the complex conjugate of the wave function with respect to x gives the probability amplitude A(p) for a given momentum. An example is provided to illustrate the concept, with the professor using cosine functions to demonstrate how the momentum values and their probabilities can be determined. The importance of normalization is also emphasized, ensuring that the integral of the probability density over all space equals one.
🤔 Addressing Confusion about Wave Function and Momentum
The professor addresses a student's confusion regarding the wave function ψ(x) and its relationship with momentum. It is clarified that ψ(x) is a function that describes the system at a given instant, while ψ_p(x) represents a particle with a definite momentum. The importance of distinguishing between the two is emphasized. The professor also explains that the probability amplitude A_p does not have to be a real number, but its absolute square, which gives the probability, is real and positive. The concept of normalization and the role of the integral in calculating probabilities are further elaborated upon.
📉 Normalization and the Quantum Particle's State
The professor delves into the process of normalizing the wave function to ensure that the integral over all space equals one, which is a requirement for a valid quantum state. Using the example of a cosine function, the professor demonstrates how to rescale the wave function and how the momentum values can be determined from the coefficients of the function. The concept of a particle being in a superposition of states with definite momentum is introduced, and it is explained that measuring the momentum will result in the wave function collapsing to a single momentum value with a certain probability.
🚫 Quantum Measurement and Wave Function Collapse
The professor explains the postulate of quantum mechanics regarding measurement, stating that upon measuring the momentum, the wave function collapses to a single term corresponding to the measured value. It is emphasized that the act of measurement changes the system. The concept of the wave function's collapse is further explored, noting that if the position is measured, the wave function becomes a spike at that position, and all other information is lost. The professor also touches on the idea that the wave function's collapse is instantaneous and that re-measuring the same property immediately would yield the same result.
🧲 The Role of the Uncertainty Principle
The professor discusses the uncertainty principle, noting that it is not mentioned as a separate postulate because it is a mathematical consequence of the wave function's properties. The principle states that the product of the uncertainties in position (Δx) and momentum (Δp) must be greater than or equal to ℏ/2. The professor connects this to the impossibility of having a well-defined position and momentum simultaneously, which is a fundamental aspect of quantum mechanics.
🌟 Energy Quantization and Atomic Transitions
The focus shifts to energy quantization, with the professor explaining that atoms can only have certain discrete energy levels. The energy difference between these levels corresponds to the energy of a photon emitted or absorbed during transitions between these states. This energy difference is given by the formula E(n=3) - E(n=1), which can be related to the frequency and wavelength of the photon. The concept of energy quantization is central to understanding atomic structure and behavior, as well as the interaction of atoms with light.
🚧 Solving the Schrödinger Equation for a Free Particle
The professor presents the Schrödinger equation for a free particle, which has no potential energy, and solves it. The solution to the equation is given in terms of exponential functions, which are related to the momentum of the particle. The professor explains that the momentum is quantized, taking on discrete values determined by an integer n, and that this quantization leads to quantized energy levels for the particle. The solution involves the concept of degeneracy, where multiple states can have the same energy.
🔍 Quantum Theory and Particle States
The professor contrasts quantum theory with classical theory regarding the momentum and energy of a particle. In classical mechanics, a particle with energy E would have a definite speed and direction, whereas in quantum mechanics, a particle can exist in a superposition of states with positive and negative momentum. The professor also addresses a student's concern about the mass of the particle and clarifies that there are no restrictions on the mass for the validity of the quantum mechanical equations.
🔵 Particle in a Box: Quantum States and Energy Levels
The professor discusses the concept of a particle in a one-dimensional box, also known as a quantum well or infinite potential well, where the particle is confined by infinitely high potential barriers. The allowed wave functions and energy levels are quantized, with the wave function being non-zero only within the box and vanishing outside. The energy levels are given by the formula ℏ²n²π²/(2mL²), where n is an integer, and the corresponding wave functions are sine functions. This example illustrates the quantization of energy in quantum mechanics and is fundamental for understanding more complex quantum systems.
Mindmap
Keywords
💡Wave Function
💡Quantum Mechanics
💡Probability Density
💡Momentum
💡Energy
💡Schrödinger Equation
💡Normalization
💡Potential Energy
💡Quantization
💡Particle in a Box
💡Linear Algebra
Highlights
The email titled 'Casaplana' from Jerry Wang and Emma Alexander inquires about the absence of time reference in wave function ψ(x) and A(p), prompting a discussion on the role of time in quantum mechanics.
Professor analogizes the state of a system in quantum mechanics to Newtonian mechanics, emphasizing the need for the wave function ψ(x) at a single instant in time to predict future states.
The complete knowledge of a particle in quantum mechanics is encapsulated by the wave function ψ(x), which is complex and can be used to predict future states.
Probability density for finding a particle is given by the absolute value squared of the wave function ψ(x), providing odds rather than a definite location.
Momentum measurement outcomes and their probabilities are derived from writing the given wave function ψ as a sum over functions ψ_p(x) with coefficients A(p).
The integral of the complex conjugate of ψ(x) with respect to x yields A(p), which is related to the probability of different momentum measurements.
Normalization of the wave function ψ(x) is crucial for obtaining meaningful probabilities, which is demonstrated through an example involving cosine functions.
The concept of measurement in quantum mechanics leads to the collapse of the wave function to a single term corresponding to the measured value.
The Heisenberg Uncertainty Principle is not explicitly stated but is a mathematical consequence of the wave function's properties.
The Schrödinger equation is introduced as the master formula for determining the functions ψ_E that correspond to definite energy states of a particle.
The energy of a particle in a given potential is found by solving the Schrödinger equation, which may yield quantized energy levels.
For a free particle (no potential), the solutions to the Schrödinger equation are plane waves, indicating a superposition of possible momenta.
The quantization of energy levels in a particle on a ring is explained, with energy levels labeled by an integer n, leading to degeneracy in energy states.
The concept of degeneracy, where multiple states share the same energy, is illustrated with the example of a particle on a ring.
The problem of a particle in a one-dimensional box is introduced as a standard quantum mechanics example to illustrate energy quantization.
The solutions to the particle in a box problem are standing waves that must satisfy boundary conditions, leading to quantized energy levels.
The particle in a box model demonstrates why energy is quantized, with only specific wavelengths fitting within the box, correlating to discrete energy levels.
Transcripts
Browse More Related Video

23. Quantum Mechanics V: Particle in a Box
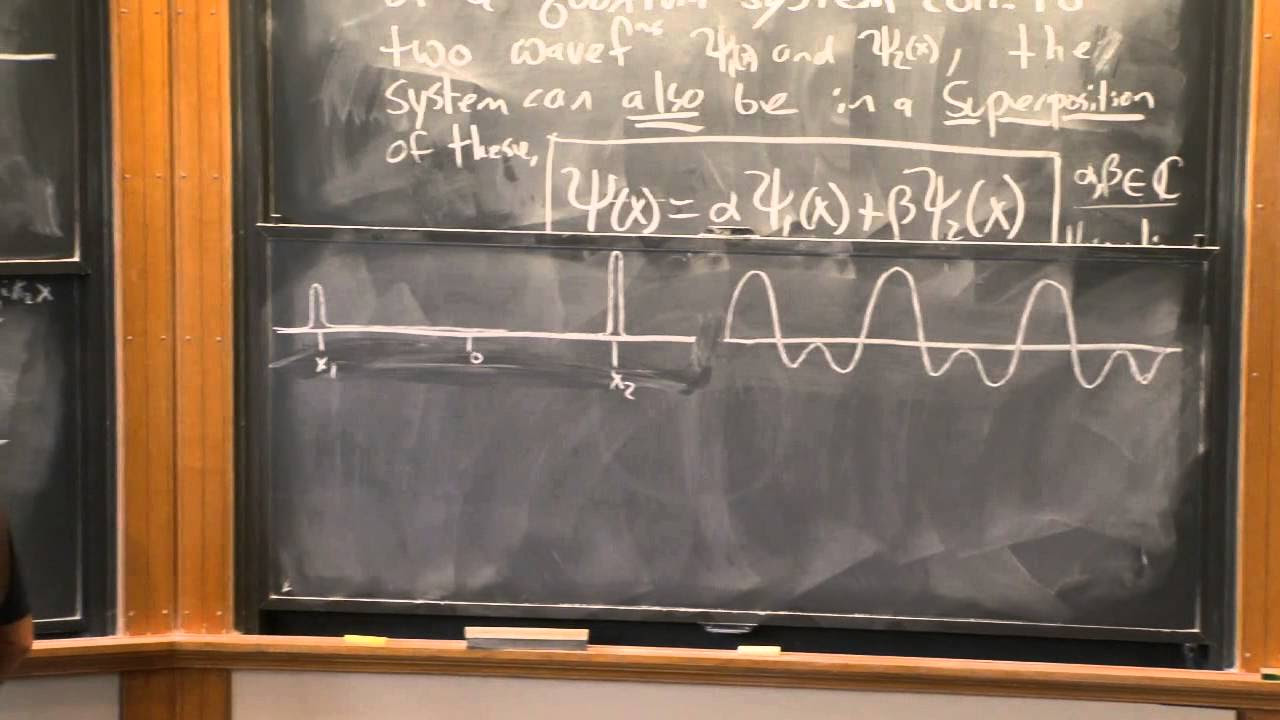
Lecture 3: The Wave Function
21. Quantum Mechanics III

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (19 of 92) Particle in 1-D Box: Example 1/2

Lecture 6: Time Evolution and the Schrödinger Equation

24. Quantum Mechanics VI: Time-dependent Schrödinger Equation
5.0 / 5 (0 votes)
Thanks for rating: