Introduction to Electric Flux

dghaase01
30 Aug 200809:05
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses two fundamental concepts in physics: electric flux and Gauss's law. Electric flux is introduced as a measure of the electric field's effect through a surface, analogous to water flow through a pipe. It emphasizes the importance of the surface's orientation relative to the electric field lines, which determines the flux magnitude. Gauss's law is presented as a tool to calculate electric fields in situations with specific symmetries, simplifying complex problems. The script aims to clarify these concepts, which are crucial for understanding not only electricity and magnetism but also other fields such as heat transfer and fluid dynamics.

Takeaways
  • πŸ“š The lecture discusses two main topics: electric flux and Gauss's law, which are independent concepts but can be used together to calculate electric fields in certain situations.
  • 🌟 Electric flux is an important concept not only in electricity and magnetism but also in other fields such as heat transfer and fluid dynamics, where it is used to describe the rate of flow.
  • 🧲 Electric flux is defined as the electric field (E) passing through a surface, with the surface's orientation and the electric field's direction affecting the amount of flux.
  • πŸ“ The surface through which the electric field lines pass is defined by a vector (A), which is perpendicular to the surface and is called the normal vector.
  • πŸ“ The magnitude of the normal vector A is equal to the area of the surface it represents.
  • πŸ” The electric flux (F) is calculated as the dot product of the electric field vector (E) and the normal vector (A), resulting in a scalar value.
  • πŸ“‰ The value of electric flux depends on the cosine of the angle between the electric field and the normal vector, with maximum flux when they are parallel and zero flux when they are perpendicular.
  • πŸ”„ If the electric field is uniform and the surface is flat, the calculation of electric flux is straightforward using the formula F = E β€’ A = |E| * |A| * cos(ΞΈ), where ΞΈ is the angle between E and A.
  • πŸ”’ The units of electric flux are Newtons per Coulomb squared (N mΒ²/C), reflecting the product of electric field strength and area.
  • πŸ“˜ Gauss's law will be used to solve for electric fields in cases with particular symmetries, allowing for quick calculations that would otherwise be very complicated.
  • πŸ”‘ The script emphasizes the importance of understanding electric flux and Gauss's law for applications in various scientific fields beyond just electricity and magnetism.
Q & A

  • What are the two main topics discussed in the script?

    -The two main topics discussed are electric flux and Gauss's law.

  • Why is understanding electric flux important for students?

    -Understanding electric flux is important because it is not only used in electricity and magnetism but also in other fields such as heat transfer and fluid dynamics, which require the same mathematical concepts.

  • What is the concept of electric flux in the context of the script?

    -Electric flux is a measure of the electric field passing through a surface, similar to the flow of water through a pipe, and it takes into account the strength of the field and the orientation of the surface.

  • How is the area of a surface related to the electric flux?

    -The area of a surface is related to the electric flux through the normal vector, which is perpendicular to the surface and its magnitude is equal to the area of the surface.

  • What is the significance of the normal vector in calculating electric flux?

    -The normal vector is significant because it defines the orientation of the surface in space and is used in the calculation of electric flux by taking the dot product with the electric field vector.

  • How does the orientation of a surface affect the electric flux?

    -The orientation of a surface affects the electric flux because the amount of electric field passing through the surface depends on the angle between the electric field lines and the normal vector of the surface.

  • What is the formula for calculating electric flux in the simple case presented in the script?

    -In the simple case, the electric flux is calculated using the formula F = E β€’ A, where E is the electric field vector, A is the normal vector, and the dot product results in a scalar value.

  • What does the dot product between the electric field and the normal vector represent?

    -The dot product between the electric field and the normal vector represents the component of the electric field that is perpendicular to the surface, which determines the electric flux through that surface.

  • How does Gauss's law relate to the calculation of electric fields?

    -Gauss's law relates to the calculation of electric fields by allowing for the solution of electric fields in cases with particular symmetries, simplifying the calculation process.

  • What is the condition for having the maximum electric flux through a surface?

    -The maximum electric flux through a surface occurs when the electric field is parallel to the normal vector of the surface, resulting in the largest possible scalar value from the dot product.

Outlines
00:00
πŸ“š Introduction to Electric Flux and Gauss's Law

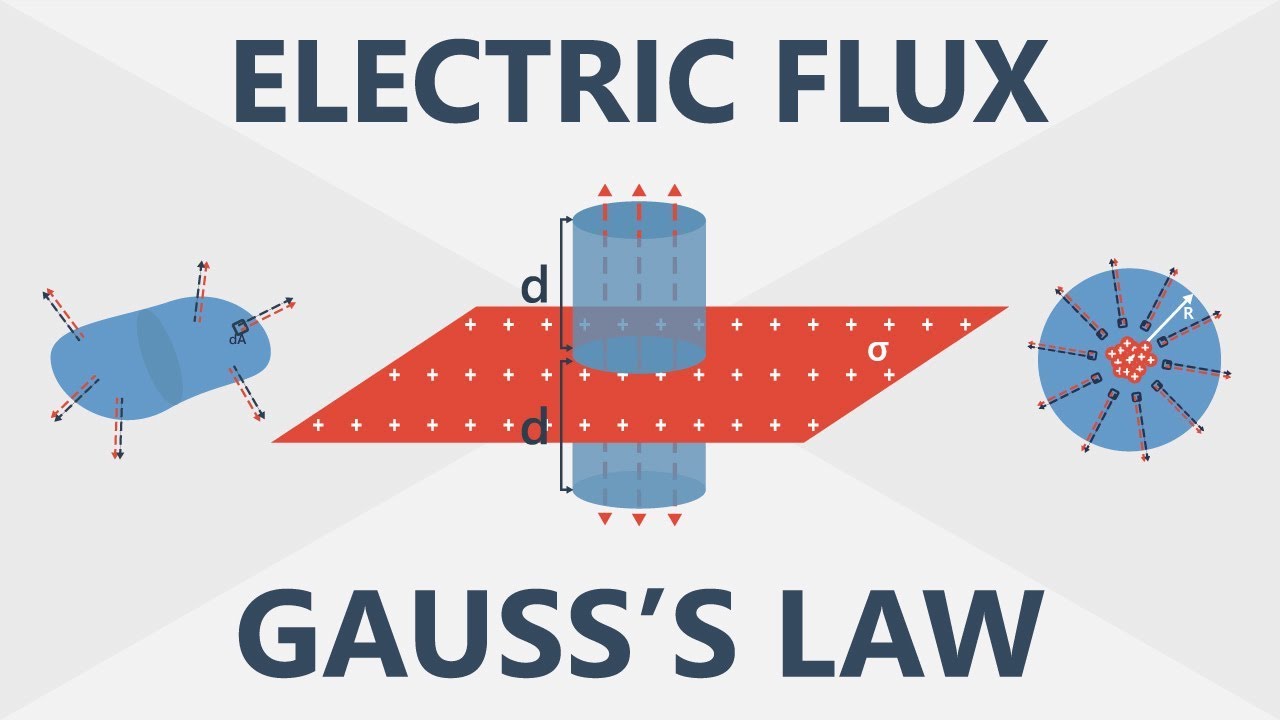
The script begins with an introduction to two fundamental concepts in the study of electric fields: electric flux and Gauss's law. The instructor emphasizes that while these are independent, they provide a comprehensive tool for calculating electric fields in various situations. The concept of electric flux is highlighted as crucial not only for electricity and magnetism but also for related fields like heat transfer and fluid dynamics. The instructor sets the stage for a detailed exploration of electric flux by comparing it to the flow of water through a pipe, suggesting that electric flux measures the 'flow' of the electric field through a surface.

05:00
πŸ” Understanding Electric Flux and Its Calculation

In this paragraph, the focus shifts to understanding how to calculate electric flux. The instructor explains that electric flux is determined by the electric field's interaction with a defined surface area. The concept of a 'normal vector' is introduced, which is perpendicular to the surface and represents its orientation in space. The magnitude of this vector corresponds to the surface area. The electric flux is then calculated as the dot product of the electric field vector and the normal vector, taking into account the angle between them. The summary clarifies that the flux is maximized when the electric field is parallel to the normal vector and minimized or zero when they are perpendicular, emphasizing the dependency of flux on the orientation of the surface relative to the electric field.

Mindmap
Keywords
πŸ’‘Electric Flux
Electric flux is a measure of the electric field's influence passing through a given surface. Defined as the dot product of the electric field (E) and a unit vector (A) perpendicular to the surface, it represents the quantity of the electric field flowing through that surface. In the video, electric flux is central to understanding how electric fields can be quantified in different orientations relative to a surface, such as when the field lines are perpendicular or parallel to the surface, affecting the magnitude of the flux.
πŸ’‘Gauss's Law
Gauss's Law relates the electric flux through a closed surface to the total charge enclosed by the surface. It is a fundamental principle in electrostatics, allowing for the calculation of electric fields in situations with symmetrical geometries. The video mentions Gauss's Law as a tool for solving complex electric field problems, particularly when the symmetry of the situation simplifies the calculations.
πŸ’‘Electric Field
An electric field is a vector field that surrounds electric charges and exerts a force on other charges within its influence. The script discusses how electric fields are produced by point charges or distributed charges and how they can be visualized with field lines. The electric field is essential for calculating electric flux, as it is one of the components in the dot product formula for flux.
πŸ’‘Vector Field
A vector field is a mathematical concept where each point in space is associated with a vector, such as the direction and magnitude of a physical quantity. In the context of the video, the electric field is an example of a vector field, and understanding vector fields is crucial for grasping the concept of electric flux, as well as for applications in other fields like fluid dynamics and heat transfer.
πŸ’‘Flux
Flux, in physics, often refers to a measure of the transfer of a physical quantity, such as heat or the flow of a fluid, across a surface. In the video, the term is used specifically to describe the electric flux, which is the transfer of the electric field's influence through a surface. The concept of flux is extended beyond electricity to other areas of physics, emphasizing its broad applicability.
πŸ’‘Surface Integral
A surface integral is a mathematical operation that generalizes the concept of integration over a surface, rather than just along a curve or in a region. In the script, the concept of surface integral is implied when discussing how to calculate electric flux by integrating over the entire surface area, taking into account the orientation of the surface relative to the electric field.
πŸ’‘Normal Vector
A normal vector is a vector that is perpendicular to a surface. In the video, the normal vector (denoted as 'a') is used to define the orientation of a surface in space and is crucial for calculating the electric flux through that surface. The magnitude of the normal vector corresponds to the area of the surface, and its direction indicates the orientation.
πŸ’‘Dot Product
The dot product is an algebraic operation that takes two equal-length vectors and returns a single number. In the context of the video, the dot product is used to calculate the electric flux, which is the product of the electric field vector and the normal vector to the surface, taking into account their relative orientation through the cosine of the angle between them.
πŸ’‘Symmetry
Symmetry in the context of the video refers to the geometric properties of a system that allow for simplifications in calculations, such as those for electric fields using Gauss's Law. When a system has symmetrical properties, it can be easier to apply Gauss's Law to find the electric field, as the symmetry can reduce the complexity of the problem.
πŸ’‘Heat Transfer
Heat transfer is the movement of heat from one place to another and is mentioned in the video as an example of another field where the concept of flux is used. The mathematics of heat transfer, like that of electric flux, involves the transfer of a quantity (in this case, heat) across a surface, making the understanding of flux relevant beyond just electricity and magnetism.
πŸ’‘Fluid Dynamics
Fluid dynamics is the study of the flow of liquids and gases. Similar to the concept of electric flux, fluid dynamics involves understanding the rate at which fluids flow through a surface, which is analogous to the calculation of electric flux. The video script mentions fluid dynamics to illustrate the broader application of the mathematical concepts introduced.
Highlights

Electric flux and Gauss's law are two independent concepts that together allow for the calculation of electric fields in complex situations with specific symmetries.

Electric flux is a crucial topic for understanding vector fields, applicable not only in electromagnetism but also in heat transfer and fluid dynamics.

Flux is defined as the electric field through a surface, akin to measuring the flow rate of water through a pipe.

The amount of electric field passing through an area depends on the orientation of the surface relative to the electric field lines.

A surface's orientation is defined by a vector perpendicular to it, known as the normal vector, with its magnitude equal to the surface area.

The electric flux is calculated using the dot product of the electric field vector and the normal vector to the surface.

The value of electric flux is a scalar, influenced by the cosine of the angle between the electric field and the normal vector.

When the electric field is parallel to the normal vector, the flux is at its maximum.

If the electric field is perpendicular to the normal vector, the flux is zero due to the cosine of 90 degrees being zero.

The concept of electric flux is fundamental for understanding the flow of electric fields and is essential for advanced calculus of vectors.

Gauss's law is introduced as a method to solve for electric fields in situations with particular symmetries, simplifying complex calculations.

The relationship between electric field strength, surface area, and orientation is crucial for calculating electric flux accurately.

Understanding the orientation of surfaces in the presence of an electric field is key to determining the flux through that surface.

The normal vector's direction changes with surface orientation, but its magnitude remains constant, representing the surface area.

The electric flux calculation is exact for flat surfaces with a constant electric field magnitude and direction over the area.

The practical applications of electric flux extend beyond physics, into engineering and environmental sciences, making it a versatile concept.

Gauss's law and electric flux are foundational for advanced studies in electromagnetism and related fields, emphasizing the importance of symmetry in problem-solving.

Transcripts

Browse More Related Video

Electric Flux (part 1)

Electric Flux

Electric flux meaning (& how to calculate it) | Electrostatics | Physics | Khan Academy

Electric Flux and Gauss’s Law | Electronics Basics #6

Physics 37.1 Gauss's Law Understood (3 of 29) What is Gauss' Law?

What is Flux? + an Introduction to Gauss Law (Electromagnetism – Physics)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Electric FluxGauss's LawPhysics ConceptsElectric FieldsVector FieldsHeat TransferFluid DynamicsSurface AreaField OrientationCalculus Vectors