21. Quantum Mechanics III

YaleCourses

23 Mar 201175:46

EducationalLearning

32 Likes 10 Comments

TLDRThe video script delves into the foundational concepts of quantum mechanics, focusing on the wave function and its implications for particle dynamics. It explains that in a one-dimensional universe, a particle's state is entirely described by its wave function, denoted as ψ. The script explores kinematics and dynamics within this quantum context, emphasizing that the wave function contains an infinite amount of information about the particle's position and momentum. The probability density function, derived from the wave function's absolute square, determines the likelihood of finding the particle at a specific location. The lecture also highlights the significance of the wave function's normalization and its role in defining quantum states. Furthermore, the script discusses the quantization of momentum in a closed system, such as a particle confined to a ring, and how this leads to the quantization of angular momentum. The uncertainty principle is introduced through the relationship between the wave function's localization in position space and the spread in momentum space, illustrating the inherent trade-off between the precision of position and momentum measurements. The script concludes with an example involving the measurement postulate, which states that the act of measurement collapses the wave function to a definite state, thereby changing the system's dynamics.

Takeaways

📐 **Wave Function Completeness**: In quantum mechanics, everything you need to know about a particle is contained in the wave function, denoted by ψ, which is more informative than classical physics' position and momentum.
⏲️ **Kinematics vs Dynamics**: Kinematics describes a system at a given time, while dynamics deals with how the system changes over time, including predicting future states.
🚀 **Quantum State Definition**: A quantum state is described by a wave function ψ that provides the probability density for finding a particle at a certain location by taking the absolute square of ψ.
🔍 **Normalization of Wave Functions**: Wave functions in quantum mechanics are normalized so that the integral of the absolute square of ψ over all space equals 1, ensuring total probability is 100%.
🌊 **Particle in a One-Dimensional Universe**: The script discusses a particle in a 1D universe for mathematical simplicity, with the understanding that higher dimensions do not significantly alter the principles.
🎚️ **Quantum State Information**: The wave function ψ can be real or complex, and from it, one can determine probabilities for different physical quantities, like position or momentum.
📉 **Probability Density**: The probability of finding a particle between two points is given by the integral of the probability density function (the absolute square of the wave function ψ) over that interval.
🚨 **Quantization of Momentum**: For a particle in a ring, the allowed values of momentum are quantized, being multiples of 2Πħ/L, where L is the circumference of the ring and ħ is the reduced Planck constant.
🔄 **Fourier Series Expansion**: Any periodic function can be expanded into a Fourier series, which in quantum mechanics allows us to express a wave function as a sum of functions, each with a definite momentum.
⚖️ **Heisenberg Uncertainty Principle**: The more precisely the position of a particle is known (the narrower the wave function in position space), the less precisely its momentum can be known (the broader the wave function in momentum space).
📝 **Measurement Postulate**: In quantum mechanics, the act of measurement affects the system. If a position or momentum is measured, the wave function collapses to a state that reflects that specific measurement.

Q & A

What is the primary function used to describe a quantum particle in one dimension?
-The wave function, denoted by the symbol ψ, is used to describe a quantum particle in one dimension. It contains all the information needed to describe the particle's quantum state.
What is kinematics in the context of particle physics?
-Kinematics is the study of describing a system completely at a given time. In classical mechanics for a single particle, the complete description is given by its position and momentum.
How does quantum theory differ from classical physics in terms of the amount of information needed to describe a particle?
-In classical physics, two numbers (position and momentum) are sufficient to describe a particle. In quantum theory, a whole function (the wave function ψ(x)) is required, which contains an infinite amount of information.
What is the significance of the absolute square of the wave function in quantum mechanics?
-The absolute square of the wave function (|ψ(x)|^2) represents the probability density of finding a particle at a specific point x. It is used to determine the likelihood of a particle's position.
What is the normalization condition for a wave function in quantum mechanics?
-The normalization condition requires that the integral of the absolute square of the wave function over all space equals 1. This ensures that the total probability of finding the particle anywhere in space is 100%.
What is the implication of the quantization of angular momentum in quantum mechanics?
-The quantization of angular momentum implies that the allowed values of angular momentum are integer multiples of ℏ (h-bar), which is a fundamental constant in quantum mechanics. This quantization is a direct result of the requirement for wave functions to be single-valued.
How does the measurement postulate in quantum mechanics affect the state of a particle?
-The measurement postulate states that upon measurement, the wave function collapses to a state that corresponds to the outcome of that measurement. If position is measured, the wave function collapses to a spike at the measured position. If momentum is measured, the wave function collapses to a state representing the measured momentum.
What is the relationship between the width of a particle's position wave function and the spread of its momentum?
-The Heisenberg Uncertainty Principle states that the more precisely the position of a particle is known (the narrower the position wave function), the less precisely its momentum can be known (the broader the spread of momentum), and vice versa.
How does the wave function of a particle change after a measurement of its position?
-After a measurement of position, the wave function collapses to a spike at the exact location where the particle was found. This means the particle is no longer 'spread out' in space but is localized at the measured position.
What is the role of Fourier series in expanding an arbitrary periodic function in quantum mechanics?
-Fourier series allows any periodic function to be written as a sum of sine and cosine functions (or complex exponentials in quantum mechanics), each with specific coefficients. These coefficients, when squared, give the probabilities of obtaining certain values when measuring dynamical variables like momentum.
Why is it not possible to have a quantum state with well-defined values for both position and momentum simultaneously?
-This is due to the Heisenberg Uncertainty Principle. States that are well-defined in position (sharp, non-broad wave functions) are broad in momentum and vice versa. The act of measuring one of these quantities (position or momentum) forces the wave function to collapse to a state that is well-defined for that quantity only.

Outlines

00:00

📚 Introduction to Quantum Kinematics

The paragraph introduces the concept of quantum kinematics, which is the study of describing a system completely at a given time. It contrasts this with classical mechanics, where the state of a particle is fully described by its position and momentum. In quantum theory, a wave function, denoted by ψ, encapsulates all knowledge about a particle. The paragraph also explains that the square of the wave function's absolute value gives the probability density of finding the particle at a certain point.

05:01

📐 Quantum States and Wave Function Normalization

This section discusses the properties of quantum states and the importance of wave function normalization. It is highlighted that the wave function can be multiplied by any complex number without changing the physical situation it represents. The concept of probability density and the requirement for the total probability to equal 1 is also explained. The paragraph further explores the conditions for different wave functions, such as those representing a particle located near a certain point or with a specific momentum.

10:01

🧮 Mathematical Challenge of Normalizing Wave Functions

The paragraph presents the mathematical challenge of normalizing wave functions that represent particles with a certain momentum. It is shown that integrating over all space for such a wave function is not possible due to the infinite extent of the universe. To circumvent this, the idea of a closed universe, modeled as a circle, is introduced. This allows for the normalization of the wave function associated with a particle confined to a ring of a certain circumference.

15:01

🔁 Single Valuedness and Quantization Condition

The discussion focuses on the condition of single valuedness for wave functions in a closed universe, leading to the quantization of momentum. It is shown that the wave function must repeat its value when going around the universe, which leads to the quantization condition pL/ℏ = 2Πm, where m is an integer. This results in the quantization of momentum, with allowed values being multiples of ℏ/L, and is identified as a fundamental aspect of quantum theory.

20:04

🌀 Angular Momentum Quantization

The paragraph connects the concept of angular momentum in quantum mechanics to the previously discussed quantization of momentum. It is stated that angular momentum, denoted by L, is an integral multiple of ℏ, a fundamental constant in quantum mechanics. The origin of this quantization is explained in the context of a particle moving in a circle, where the momentum times the radius equals mℏ, highlighting the deep connection between quantum mechanics and angular momentum.

25:05

🎢 Wave Function and Momentum Measurement

This section explores the relationship between an arbitrary wave function and the probabilities associated with measuring the momentum of a particle. It introduces the postulate that the probability of obtaining a certain momentum value is given by the square of the coefficient in the wave function's expansion in terms of momentum eigenstates. The paragraph also emphasizes the importance of squaring the wave function to obtain probabilities and touches upon the concept of Fourier series.

30:08

📓 Fourier Series and Coefficients

The paragraph delves into the mathematical foundation of Fourier series, which allows any periodic function to be represented as a sum of trigonometric functions with specific coefficients. It is shown how the coefficients of these functions can be determined using integrals and the concept of Kronecker's delta. The analogy between expanding a vector in three dimensions and a function in terms of basis functions is highlighted.

35:09

🔍 Measurement Postulate and Wave Function Collapse

The final paragraph introduces the measurement postulate of quantum mechanics, which states that upon measurement, the wave function collapses to a state corresponding to the measured value. This implies that the act of measurement affects the quantum state. The postulate is illustrated with examples of measuring position and momentum, showing how the wave function adjusts to reflect the definite outcome of the measurement. It also touches upon the impossibility of simultaneously knowing precise values of position and momentum, which is a manifestation of the Heisenberg uncertainty principle.

Mindmap

Keywords

💡Wave Function

The wave function, denoted by the Greek letter ψ (psi), is a fundamental concept in quantum mechanics. It encodes the complete physical description of a particle in a quantum state. In the script, the wave function is discussed as containing all the information about a particle's position and momentum, with its absolute square representing the probability density of finding the particle at a certain point in space.

💡Kinematics

Kinematics is the study of motion without considering the forces that cause the motion. In the context of the video, it is used to describe the state of a system completely at a given time, such as the position and momentum of a particle. The script explains that in classical mechanics, this would be enough to predict future states, but in quantum mechanics, a wave function is required.

💡Dynamics

Dynamics is the branch of physics that deals with the forces that cause motion and the subsequent effects of those forces. In the script, it is mentioned in contrast to kinematics, focusing on how the state of a particle changes over time. The question of whether one can predict the future by knowing the current state is central to the dynamics of quantum systems.

💡Quantum State

A quantum state is a state of a quantum system described by a wave function. The script emphasizes that in quantum mechanics, a particle's state is not known with certainty but is given in terms of probabilities, which are derived from the wave function. The quantum state is a central element in understanding the probabilistic nature of quantum mechanics.

💡Probability Density

In quantum mechanics, the probability density is the absolute square of the wave function, which describes the likelihood of finding a particle in a particular location. The script explains that multiplying the wave function by an infinitesimal Δx gives the probability that the particle will be between x and x + Δx.

💡Normalization

Normalization in quantum mechanics is the process of scaling the wave function so that the total probability of finding the particle in all possible states adds up to 1. The script discusses the importance of normalization for ensuring that the wave function provides meaningful probabilities when squared.

💡Momentum

Momentum is a physical quantity that represents the motion of an object. In the script, it is discussed in the context of quantum mechanics, where the momentum of a particle is related to the wave function through the de Broglie relation. The script also touches on the quantization of momentum in a ring, which is a key concept in understanding the behavior of particles in confined spaces.

💡Quantization

Quantization refers to the process by which a physical quantity can only take on discrete values. In the script, the quantization of momentum for a particle in a ring is explained, showing that the momentum can only take on certain allowed values, which are integer multiples of a fundamental quantum. This concept is crucial for understanding the discrete energy levels in quantum systems.

💡Fourier Series

A Fourier series is a mathematical tool used to represent a periodic function as an infinite sum of sine and cosine functions. In the script, it is mentioned in the context of expanding a given wave function into a sum of functions, each with a definite momentum. This expansion allows one to calculate the probability distribution of different momentum values for a particle.

💡Measurement Postulate

The measurement postulate in quantum mechanics states that the act of measurement affects the quantum system. The script describes how the wave function collapses to a specific state upon measurement. For instance, if the position is measured, the wave function collapses to a spike at the measured position, and if the momentum is measured, the wave function collapses to a state with a definite momentum.

💡Uncertainty Principle

The uncertainty principle, as discussed in the script, is a fundamental concept in quantum mechanics that states there is a limit to the precision with which certain pairs of physical properties of a particle, like position and momentum, can be known. The script illustrates this principle by showing that a particle with a well-defined position has a broad range of possible momenta and vice versa.

Highlights

Introduction to quantum mechanics through the study of a particle in one dimension, emphasizing the mathematical simplicity and sufficient complexity for understanding quantum behavior.

Explanation of the wave function (ψ) as the fundamental description containing all information about a quantum particle, contrasting with classical physics' position and momentum.

Introduction of kinematics in quantum mechanics, which describes a system completely at a given time, analogous to classical mechanics but using the wave function.

Discussion on dynamics, which involves predicting future states of a quantum system based on current knowledge, a key question in quantum theory.

The concept that the wave function can be real or complex, and its absolute square represents the probability density of finding a particle at a certain point.

Total probability to find a particle anywhere is conventionally set to 1, allowing for the interpretation of the wave function's square as a probability density function.

The principle that the wave function ψ and any multiple of it represent the same physical situation, highlighting the importance of the relative, not absolute, values in quantum mechanics.

The conditions for possible wave functions of a particle, emphasizing single-valuedness and continuity, which are key for describing quantum states.

The use of Fourier series to expand any periodic function into a sum of trigonometric functions, a powerful tool for analyzing quantum states.

The quantization of momentum for a particle in a ring, leading to the concept that only certain discrete values of momentum are allowed, a fundamental aspect of quantum theory.

The relationship between angular momentum and its quantization in units of ℏ, derived from the single-valuedness condition of the wave function.

The collapse of the wave function upon measurement, illustrating how the act of measurement affects the quantum state, leading to a post-measurement state that is an eigenfunction of the measured observable.

The uncertainty principle is mathematically derived from the properties of wave functions in position and momentum space, showing that a narrow position wave function corresponds to a broad range of momenta.

The concept that measurement outcomes are restricted to the set of allowed values for the observable being measured, which are determined by the quantum state of the system.

The role of measurement in quantum mechanics as a way to prepare a state with a definite value of an observable, emphasizing the probabilistic nature of quantum states.

The illustration of how the wave function collapses to a specific momentum state upon measurement of momentum, and how this collapse is described by a plane wave with a definite quantum number m.

The final example demonstrates the calculation of the wave function collapse for a particle in a ring with a specific Gaussian wave function, showing the interplay between position and momentum uncertainties.

Transcripts

Browse More Related Video

22. Quantum mechanics IV: Measurement theory, states of definite energy

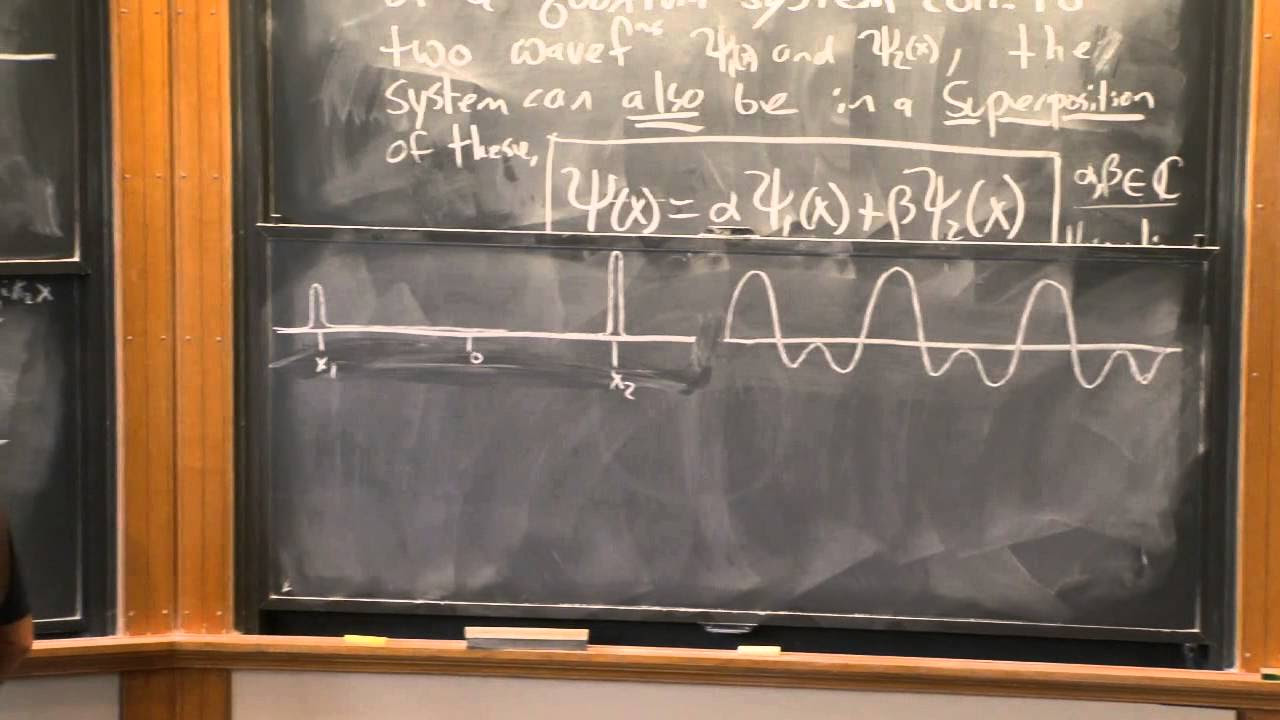
Lecture 3: The Wave Function

19. Quantum Mechanics I: The key experiments and wave-particle duality

23. Quantum Mechanics V: Particle in a Box

What is the Heisenberg Uncertainty Principle? A wave packet approach

Visualization of Quantum Physics (Quantum Mechanics)

Related Tags

Quantum Mechanics Wave Function Probability Density Heisenberg Uncertainty Momentum Kinematics Dynamics Fourier Series Complex Exponentials Normalization Measurement Postulate