Physics 37.1 Gauss's Law Understood (4 of 29) Gauss' Law Clarified

Michel van Biezen
14 Feb 201805:34
EducationalLearning
32 Likes 10 Comments

TLDRThe video script offers a detailed explanation of Gauss's law in the context of electricity. It describes how the electric flux, represented by electric field lines, remains constant regardless of the size of the Gaussian surface around a point charge. The script explains that the electric field strength can be determined by the charge and the distance from it, using the formula E = kQ/r^2, where k is a constant related to the permittivity of free space. The key takeaway is that Gauss's law allows us to calculate the electric field around any charged object by drawing a Gaussian surface and using the relationship between electric flux, charge, and the surface area.

Takeaways
  • 🔋 Gauss's law helps us understand the relationship between electric flux and electric fields around a point charge.
  • 🔵 The electric field around a point charge emanates radially outward in all directions.
  • 🔄 Electric flux through a Gaussian surface is constant regardless of the surface's radius.
  • 📏 Electric flux is the product of the electric field strength and the area of the surface.
  • 🌀 As the radius of the Gaussian surface increases, the electric field strength decreases, but the surface area increases proportionally.
  • 🔋 The electric field of a point charge is given by KQ/r², where K is 1/4πϵ₀ and ϵ₀ is the permittivity of free space.
  • 🧮 Electric flux can be expressed as the charge inside the Gaussian surface divided by ϵ₀.
  • 🌐 Gauss's law states that the electric flux through a Gaussian surface is equal to the enclosed charge divided by ϵ₀.
  • 📐 For a spherical Gaussian surface, the area is 4πr², and this helps simplify calculations of electric flux and field strength.
  • ⚡ Using Gauss's law, we can determine the electric field at any point around a charged object by drawing an appropriate Gaussian surface.
Q & A

  • What is Gauss's law and how does it relate to electric fields?

    -Gauss's law, also known as Gauss's flux theorem, states that the electric flux through any closed surface is proportional to the total charge enclosed by the surface. It is a fundamental law in electromagnetism that relates the electric field to the charge distribution.

  • What is a Gaussian surface and why is it used in Gauss's law?

    -A Gaussian surface is an imaginary closed surface used in the application of Gauss's law. It is used to calculate the electric flux through the surface, which is a measure of the electric field's influence through that surface.

  • How does the electric field around a point charge behave?

    -The electric field around a point charge emanates radially outward from the charge. The electric field lines are perpendicular to the surface of the charge and spread out uniformly in all directions.

  • What is the relationship between electric flux and the electric field strength?

    -Electric flux is defined as the product of the electric field strength (E) and the area (A) through which the field lines pass. It represents the total influence of the electric field through a given area.

  • Why is the electric flux through a Gaussian surface constant regardless of its size?

    -The electric flux through a Gaussian surface is constant because the number of electric field lines passing through the surface does not change with the size of the surface. The weakening of the field with distance is compensated by the increase in surface area.

  • What is the formula for the electric field of a point charge?

    -The electric field (E) of a point charge (Q) is given by the formula E = kQ / r^2, where k is Coulomb's constant and r is the distance from the charge.

  • What is the significance of the permittivity of free space (ε₀) in Gauss's law?

    -The permittivity of free space (ε₀) is a constant that relates the electric field to the charge distribution. It appears in the formula for Coulomb's law and Gauss's law, and it quantifies the ability of free space to permit the electric field.

  • How does the area of a Gaussian surface affect the calculation of electric flux?

    -The area of the Gaussian surface is directly proportional to the electric flux. As the area increases, the total electric flux through the surface also increases, assuming the enclosed charge remains constant.

  • Can you explain the cancellation of the 'r' terms in the calculation of electric flux for a spherical Gaussian surface?

    -When calculating the electric flux for a spherical Gaussian surface, the r^2 term in the denominator of the electric field formula (E = kQ / r^2) cancels with the r^2 term in the area formula of the sphere (4πr^2), simplifying the expression for electric flux.

  • What is the final simplified form of Gauss's law for a point charge?

    -The final simplified form of Gauss's law for a point charge is E * A = Q / ε₀, where E is the electric field strength, A is the area of the Gaussian surface, Q is the enclosed charge, and ε₀ is the permittivity of free space.

  • How can Gauss's law be used to find the electric field strength around a point charge?

    -Gauss's law can be used to find the electric field strength by drawing a Gaussian surface around the point charge and using the relationship E = Q / (ε₀ * A). Since the flux (E * A) is constant and equal to Q / ε₀, the electric field strength can be determined.

Outlines
00:00
🔋 Understanding Gauss's Law with Point Charge

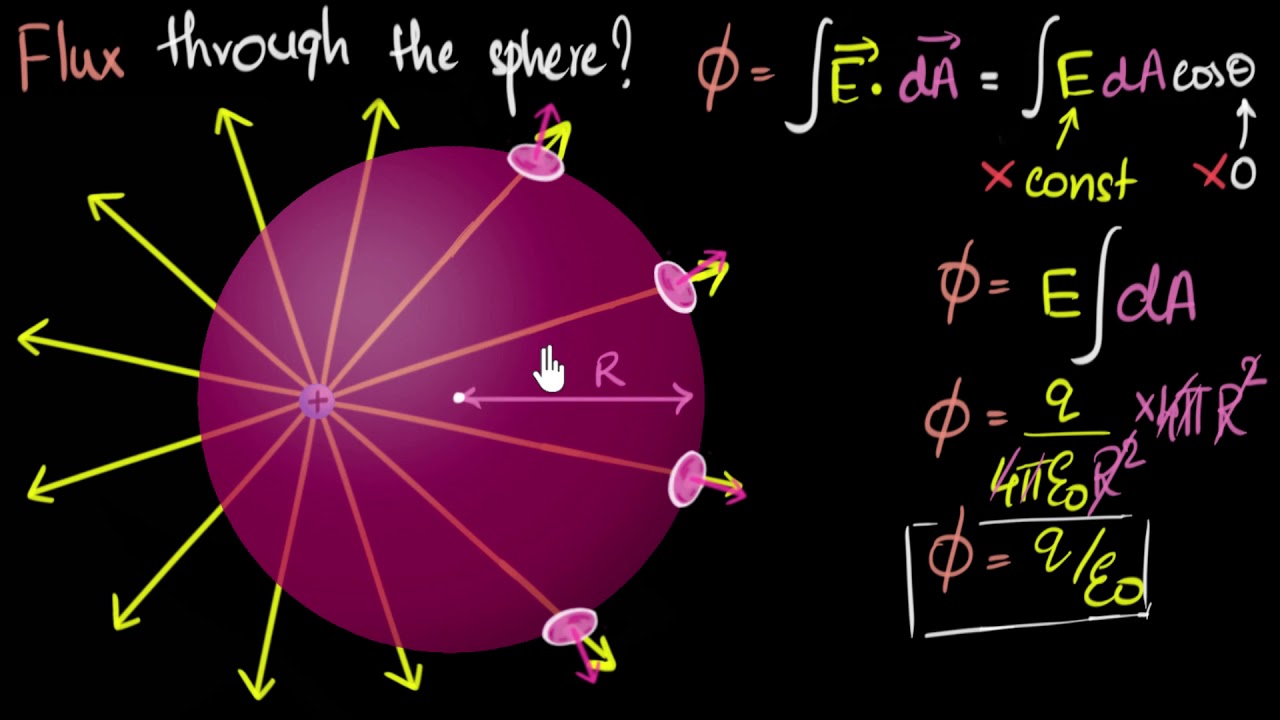
This paragraph explains the fundamental concept of Gauss's law in the context of a point charge, denoted as Q. It introduces the idea of placing Gauss's surfaces at various radii around the charge and describes how the electric field lines emanate from the charge, perpendicularly in all directions. The paragraph clarifies that the electric flux, which is the product of the electric field strength and the area of the surface, remains constant regardless of the size of the Gaussian surface due to the unchanging number of electric field lines. It also explains the mathematical relationship between the electric field of a point charge, the permittivity of free space, and the constant K, which is derived from Coulomb's law. The summary concludes with the derivation of Gauss's law, which states that the electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space.

05:02
📚 Practical Application of Gauss's Law

The second paragraph delves into the practical application of Gauss's law, emphasizing its simplicity and utility in determining the electric field of any charge using Gaussian surfaces. It suggests that understanding Gauss's law allows for the calculation of the electric field strength around a point charge by drawing a Gaussian surface and applying the principles discussed in the first paragraph. The paragraph also reiterates the importance of Gauss's law in providing a constant measure of electric flux, which is a product of the electric field strength and the surface area of the Gaussian surface. It concludes with a brief mention of further examples that will be provided to clarify the application of Gauss's law, hinting at the educational nature of the content that follows.

Mindmap
Keywords
💡Gauss's Law
Gauss's Law relates the electric flux through a closed surface to the charge enclosed by that surface. In the video, it is demonstrated through the example of point charge Q and how electric flux remains constant regardless of the Gaussian surface's size. It underscores the principle that electric field strength multiplied by the area of the surface equals the charge enclosed divided by the permittivity of free space.
💡Point Charge
A point charge refers to an electric charge considered to be concentrated at a single point in space. In the video, the point charge Q serves as the source of the electric field being analyzed with various Gaussian surfaces. The concept is crucial for understanding how electric fields and fluxes behave in relation to Gauss's Law.
💡Electric Field
An electric field is a vector field around a charged object where a force would be exerted on other charges. The video describes how the electric field lines emanate radially from a point charge and how its strength is calculated as KQ/r², where K is a constant. The understanding of electric fields is fundamental to applying Gauss's Law.
💡Gaussian Surface
A Gaussian surface is an imaginary closed surface used in Gauss's Law to calculate electric flux. The video shows different Gaussian surfaces with varying radii around a point charge, illustrating that the electric flux through these surfaces remains constant. This concept helps visualize the application of Gauss's Law in determining the electric field.
💡Electric Flux
Electric flux is the measure of the number of electric field lines passing through a surface. In the video, it's defined as the product of the electric field strength and the area of the surface (E × A). The constant nature of electric flux through any Gaussian surface around a point charge is a key takeaway from Gauss's Law.
💡Permittivity of Free Space (ε₀)
The permittivity of free space, denoted as ε₀, is a constant that characterizes the strength of the electric field in a vacuum. In the video, it is part of the formula for electric flux and electric field calculations, showing how charge inside a Gaussian surface divided by ε₀ gives the electric flux. It is essential for understanding the constants involved in Gauss's Law.
💡Surface Area
Surface area in the context of Gauss's Law refers to the area of the Gaussian surface through which the electric flux is calculated. The video illustrates this with spherical surfaces, using the formula 4πr² for the area of a sphere. Understanding surface area is critical for calculating electric flux and applying Gauss's Law.
💡Electric Field Lines
Electric field lines are a visual representation of the direction and strength of an electric field. The video uses red arrows to depict how these lines emanate perpendicularly from a point charge in all directions. The concept helps in visualizing how electric fields interact with Gaussian surfaces in Gauss's Law.
💡K (Coulomb's Constant)
Coulomb's constant, denoted as K, is a proportionality constant in Coulomb's law of electric force. In the video, it's used in the formula KQ/r² to calculate the electric field strength around a point charge. Understanding K is necessary for solving problems involving electric fields and forces.
💡Radii
Radii refer to the distances from the center of the point charge to the Gaussian surfaces. The video uses different radii (R1, R2) to show that electric flux remains constant regardless of the radius of the Gaussian surface. This concept helps demonstrate the inverse relationship between field strength and surface area in Gauss's Law.
Highlights

Introduction of Gauss's law and its significance in understanding the electric field around a point charge.

Explanation of the concept of a Gaussian surface and its use in calculating electric flux.

Description of electric field lines emanating from a point charge and their representation.

The constancy of electric flux through a Gaussian surface regardless of its size.

The relationship between electric field strength, surface area, and electric flux.

The formula for the electric field of a point charge and its derivation.

The definition of the constant K in terms of the permittivity of free space.

Calculation of electric flux using the formula for electric field strength and the area of a sphere.

The cancellation of terms in the electric flux equation leading to a simplified expression.

Gauss's law as a fundamental principle linking electric flux, charge, and the permittivity of free space.

The method to determine the electric field magnitude using the electric flux and surface area.

Rederivation of the point charge electric field equation using Gauss's law.

Gauss's realization and its practical application in determining the electric field around any charged object.

The demonstration of simple examples to clarify the application of Gauss's law.

The conclusion emphasizing the ease of using Gaussian surfaces to determine the electric field strength.

Transcripts

Browse More Related Video

Physics 37.1 Gauss's Law Understood (3 of 29) What is Gauss' Law?

Gauss law of electricity | Electrostatics | Physics | Khan Academy

Gauss Law Problems, Cylindrical Conductor, Linear & Surface Charge Denisty, Electric Field & Flux,

Physics 37.1 Gauss's Law Understood (5 of 29) How to Use Gauss' Law

Electric Field of a Sphere

Electric Flux and Gauss’s Law | Electronics Basics #6

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Gauss's LawElectric FluxPoint ChargeElectric FieldEpsilon NoughtGaussian SurfacePhysics ConceptElectromagnetismField TheoryEducational Content