Physics 37.1 Gauss's Law Understood (3 of 29) What is Gauss' Law?

Michel van Biezen
13 Feb 201806:30
EducationalLearning
32 Likes 10 Comments

TLDRThis script explores Gauss's Law in the context of electromagnetism, using the analogy of an imaginary sphere placed around a point charge. It explains how the electric field's strength times the sphere's surface area equals the enclosed charge divided by the permittivity of free space (ε₀). The law implies that the electric flux through any closed surface is proportional to the charge enclosed, regardless of the surface's size. The script also touches on the integral form of Gauss's Law and its applications in solving complex problems involving electric fields.

Takeaways
  • 🌐 Gauss's Law is best visualized by imagining an imaginary sphere placed around a point charge.
  • 📍 The size of the imaginary sphere (Gaussian surface) does not affect the fundamental principle of Gauss's Law.
  • 🔋 Gauss's Law is mathematically expressed as the electric field strength (E) times the surface area (A) equal to the charge (Q) divided by the permittivity of free space (ε₀).
  • 📈 The electric field's magnitude at the surface of the Gaussian sphere depends on the distance from the charge; closer means stronger field.
  • ⚪ The Gaussian surface is considered to have a uniform electric field pointing perpendicularly outwards from the surface.
  • 🔗 The number of electric field lines emanating from a charge is constant regardless of the size of the Gaussian surface.
  • 📚 The permittivity of free space (ε₀) is a constant, approximately 8.85 × 10^-12 C²/Nm², representing the proportionality in Gauss's Law.
  • 🔍 Gauss's Law can be written in an integral form, which involves integrating the dot product of the electric field and a small area element over the entire surface.
  • 🛠 The law is particularly useful for solving problems involving electric fields that would be difficult to approach without it.
  • 📉 The flux through the surface, defined as the product of the electric field strength, area, and cosine of the angle between them, remains constant for any Gaussian surface around a point charge.
  • 🔑 Gauss's Law provides a direct relationship between the enclosed charge and the electric field distribution on the Gaussian surface, simplifying complex calculations.
Q & A

  • What is Gauss's Law?

    -Gauss's Law, also known as Gauss's flux theorem, states that the total electric flux through any closed surface is proportional to the total charge enclosed within the surface, divided by the permittivity of free space (ε₀).

  • What is the significance of an imaginary sphere in Gauss's Law?

    -An imaginary sphere in Gauss's Law is a conceptual tool used to simplify the problem of calculating electric flux. It is a closed surface that can be of any size and is used to enclose a point charge, allowing for the application of Gauss's Law to find the electric field.

  • How is the electric field related to the charge enclosed by a Gaussian surface?

    -The electric field at any point on the Gaussian surface is directly proportional to the charge enclosed by the surface and inversely proportional to the square of the distance from the charge, assuming the charge is at the center of the sphere.

  • What is the equation that defines Gauss's Law when dealing with a point charge at the center of a Gaussian sphere?

    -The equation that defines Gauss's Law in this scenario is E * A = Q / ε₀, where E is the magnitude of the electric field, A is the surface area of the sphere, Q is the charge enclosed, and ε₀ is the permittivity of free space.

  • What is the permittivity of free space (ε₀) and what is its value?

    -The permittivity of free space (ε₀) is a physical constant that describes the ability of free space to permit the formation of an electric field. Its value is approximately 8.85 × 10⁻¹² C²/N·m².

  • How does the size of the Gaussian surface affect the magnitude of the electric field?

    -The magnitude of the electric field is inversely proportional to the square of the radius of the Gaussian surface. As the surface gets larger (further from the charge), the electric field strength decreases.

  • What is the direction of the electric field on the surface of a Gaussian sphere?

    -The electric field on the surface of a Gaussian sphere is directed perpendicular to the surface at every point, pointing radially outward if the charge is positive, and inward if the charge is negative.

  • What is the concept of electric flux?

    -Electric flux is a measure of the electric field that passes through a given surface. It is defined as the dot product of the electric field and the area vector perpendicular to the surface, and is a scalar quantity.

  • Why is the number of electric field lines constant through any Gaussian surface regardless of its size?

    -The number of electric field lines is constant because it is proportional to the enclosed charge. Regardless of the size of the Gaussian surface, the total charge enclosed remains the same, hence the number of electric field lines passing through the surface is constant.

  • How can Gauss's Law be written in integral form?

    -In integral form, Gauss's Law is written as ∮E • dA = Q_enclosed / ε₀, where the integral is taken over the closed surface, E is the electric field, dA is a differential area element, and Q_enclosed is the total charge enclosed by the surface.

  • What is the practical application of Gauss's Law in solving electric field problems?

    -Gauss's Law simplifies the calculation of electric fields for symmetrical charge distributions, such as spherical, cylindrical, or planar geometries. It allows for direct calculation of the electric field without needing to integrate over the entire space.

Outlines
00:00
🌐 Introduction to Gauss's Law

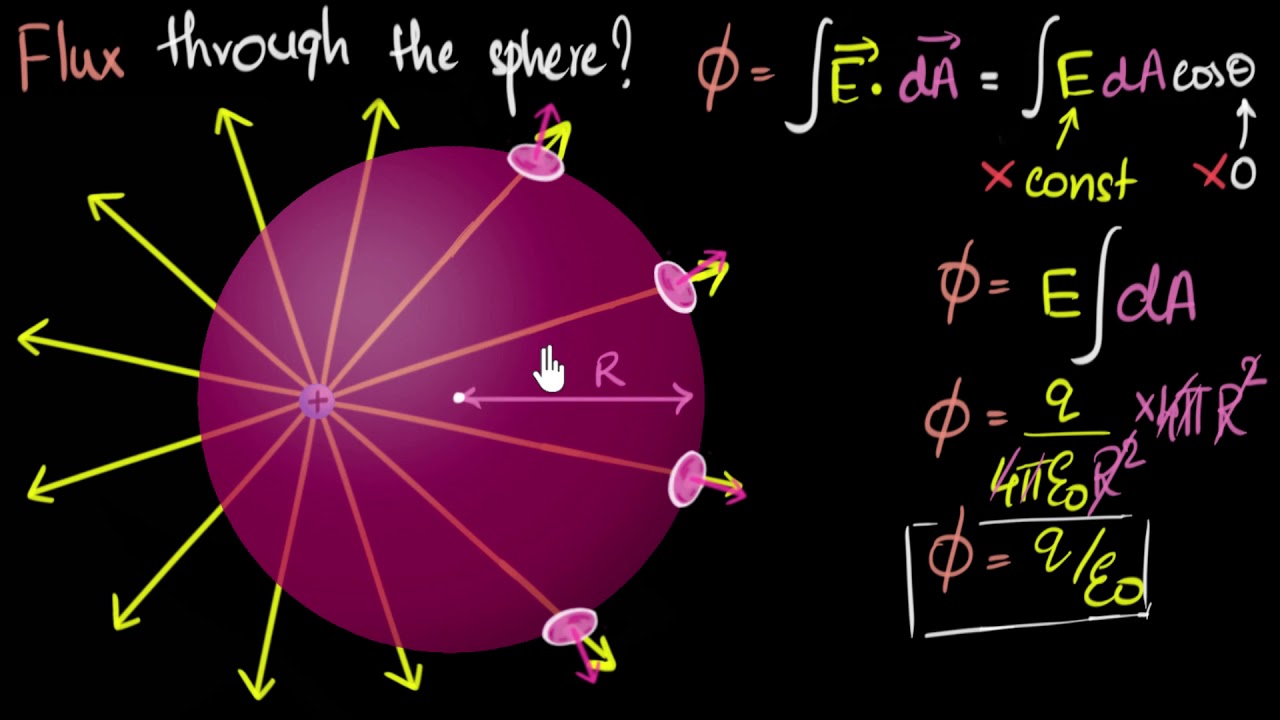
This paragraph introduces Gauss's law by visualizing an imaginary sphere placed around a point charge. It explains that the electric field's strength times the sphere's surface area equals the charge enclosed divided by the permittivity of free space (epsilon sub naught). The permittivity is a constant, approximately 8.85 x 10^-12 C²/Nm². The paragraph emphasizes that the electric field is perpendicular to the Gaussian surface and that the number of electric field lines through any Gaussian surface is constant, regardless of its size, and is proportional to the enclosed charge.

05:02
🔍 Gauss's Law in Practice

The second paragraph delves into the practical application of Gauss's law, highlighting its utility in solving complex problems related to electric fields. It clarifies that for a charge placed at the center of a Gaussian surface, the electric field is uniform and perpendicular to the surface. The integral form of Gauss's law is also mentioned, which involves integrating the electric field over a surface. The paragraph assures that understanding Gauss's law and electric flux is fundamental to solving a variety of problems in the field of electromagnetism.

Mindmap
Keywords
💡Gauss's Law
Gauss's Law, also known as the flux theorem, is a fundamental principle in electromagnetism that quantifies the relationship between the electric field and the charge that produces it. In the video, Gauss's Law is described as the equation relating the electric field's strength times the area of an imaginary sphere (Gaussian surface) to the charge enclosed by the sphere divided by the permittivity of free space. It is central to the video's theme, as it is the main concept being explained.
💡Electric Field
The electric field is a vector field that surrounds electrically charged particles and exerts a force on other charged particles within the field. In the context of the video, the electric field's magnitude is discussed in relation to the distance from the charge, with the field being stronger closer to the charge. It is a key component in understanding Gauss's Law, as the law involves the electric field's strength at the surface of a Gaussian sphere.
💡Point Charge
A point charge refers to an idealized model of a charged particle where the size of the particle is negligible compared to the distances involved in the problem at hand. In the script, a point charge is used to illustrate the concept of Gauss's Law, with an imaginary sphere placed around it to demonstrate how the electric field behaves in relation to the charge.
💡Gaussian Surface
A Gaussian surface is an imaginary closed surface used in the application of Gauss's Law to visualize and calculate the electric flux through the surface. The video explains that the electric field is perpendicular to this surface, and the flux is constant regardless of the size of the sphere, as long as the charge is at the center.
💡Flux
Flux, in the context of electromagnetism, is a measure of the amount of a field (such as the electric field) passing through a given surface. The video describes flux as the product of the electric field strength, the area of the surface, and the cosine of the angle between them. It is a critical concept in understanding how Gauss's Law relates the electric field to the enclosed charge.
💡Permittivity of Free Space
The permittivity of free space, denoted as epsilon sub naught (ε₀), is a physical constant that relates the electric field in a vacuum to the electric displacement field. In the video, it is used in Gauss's Law as the proportionality constant that allows the calculation of the electric field from the charge enclosed by the Gaussian surface.
💡Electric Field Lines
Electric field lines are a visual representation used to describe the direction and relative strength of the electric field. The video mentions that the number of electric field lines emanating from a charge is proportional to the amount of charge, and this number remains constant regardless of the size of the Gaussian surface drawn around the charge.
💡Charge
Charge is a fundamental property of matter that gives rise to electric forces and fields. The video script discusses how the amount of charge affects the strength of the electric field and the number of electric field lines. It is the source of the electric field and the quantity that Gauss's Law relates to the electric field through the Gaussian surface.
💡Integral Form
The integral form of Gauss's Law involves integrating the dot product of the electric field and a small area element over a closed surface. In the video, this form is mentioned as an alternative way to express the law, particularly useful when the electric field is not uniform or when the charge distribution is complex.
💡Dot Product
The dot product is a mathematical operation that takes two vectors and returns a scalar. In the context of the integral form of Gauss's Law, the dot product is used to calculate the component of the electric field that is perpendicular to the area element on the Gaussian surface, which is essential for determining the electric flux.
💡Magnitude
The magnitude of a vector quantity, such as the electric field, is its length or size without considering direction. The video explains that the magnitude of the electric field at the surface of the Gaussian sphere is used in Gauss's Law to calculate the electric flux through the surface.
Highlights

Introduction to Gauss's law concept with an imaginary sphere around a point charge.

Gauss's law definition involving the electric field, charge, and the permittivity of free space.

Explanation of the electric field strength's dependency on the size of the Gaussian surface.

The electric field's direction is always perpendicular to the surface of the Gaussian sphere.

Constant number of electric field lines through any Gaussian surface regardless of its size.

Flux is the product of electric field strength, area of the surface, and the constant number of electric field lines.

Gauss's law's integral form involving the dot product of electric field and area element.

Gauss's law's practical application in solving problems involving electric fields.

The necessity of placing the charge at the center of the Gaussian surface for the law to apply simply.

The importance of the electric field pointing perpendicular to the Gaussian surface for the equation's simplification.

The proportionality constant, epsilon sub naught, in Gauss's law representing the permittivity of free space.

The value of epsilon sub naught as 8.85 × 10^-12 coulombs square per newton meter square.

Gauss's law's significance in physics for understanding electric flux and field distribution.

The conceptual understanding required before applying Gauss's law to practical problems.

The presentation of examples to enhance understanding of Gauss's law application.

Transcripts

Browse More Related Video

Gauss law of electricity | Electrostatics | Physics | Khan Academy

Gauss law logical proof (any closed surface) | Electric charges & fields | Physics | Khan Academy

Ultimate Gauss' Law review

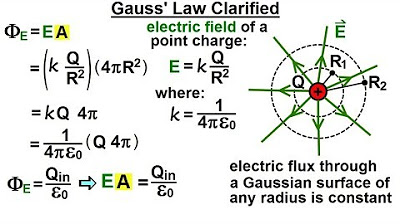
Physics 37.1 Gauss's Law Understood (4 of 29) Gauss' Law Clarified

Electric Flux and Gauss’s Law | Electronics Basics #6

Electric Flux (part 1)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Gauss's LawElectric FieldImaginary SpherePoint ChargePhysics ConceptFlux CalculationSurface AreaCharge EnclosedEpsilon NaughtField LinesElectrostatics