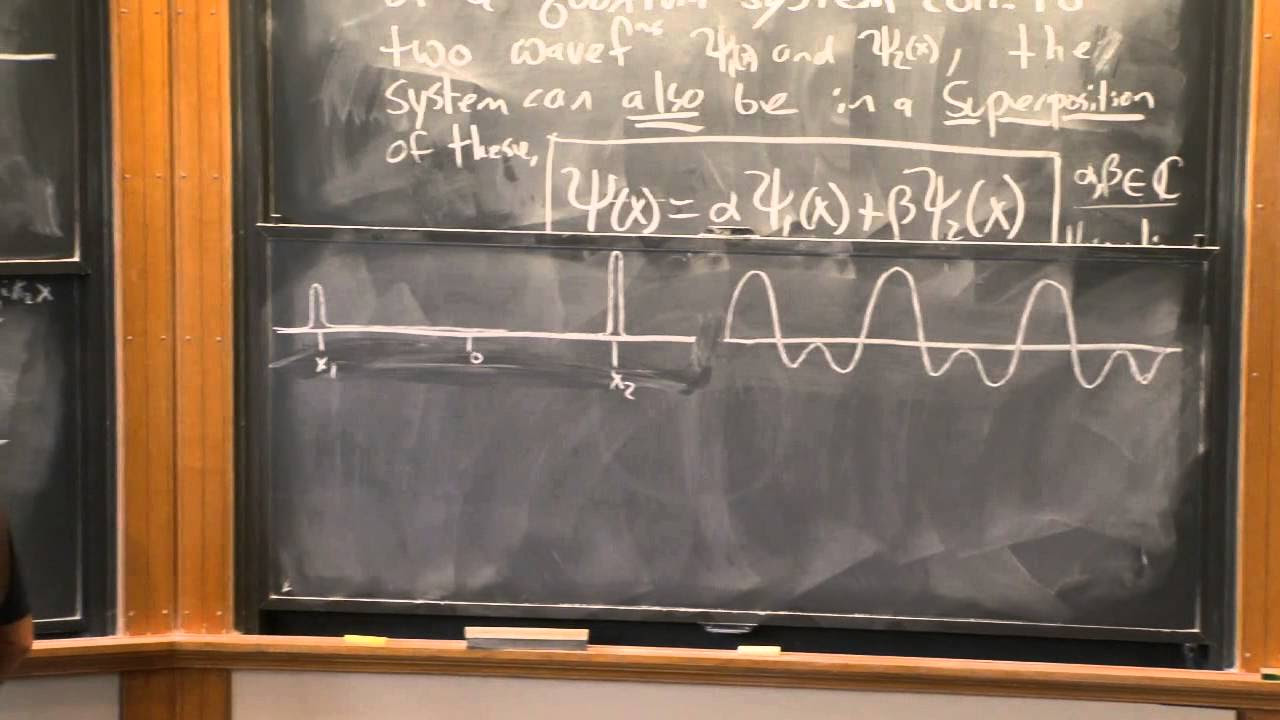Lecture 5: Operators and the Schrödinger Equation
TLDRThe transcript outlines a lecture on quantum mechanics, focusing on the Schrodinger equation and key concepts such as wave functions, probability, superposition, and operators. It explains how particles are described by wave functions, the association of probability with wave functions, and the principle of superposition. The lecture delves into the role of operators in quantum mechanics, introducing the idea of eigenfunctions and eigenvalues, and their significance in measurement outcomes. The non-commutability of certain operators, like position and momentum, is highlighted, leading to the introduction of the Heisenberg uncertainty principle. The lecture culminates in the derivation of the Schrodinger equation, emphasizing its fundamental role in determining the time evolution of quantum states.
Takeaways
- 🌟 Quantum mechanics is based on the idea that particles are governed by wave functions, which are complex numbers and must be continuous and normalizable.
- 🎯 The probability of finding a particle at a specific point is generally zero; instead, we consider the probability of finding it within a range, given by the square of the wave function.
- 📈 Superposition of states is a fundamental concept, where a system can be in a combination of multiple states simultaneously, such as a particle being in multiple positions or a photon being polarized in multiple directions.
- 🔄 The momentum operator (p-hat) is associated with the particle's momentum and is represented as the operator h-bar over i times the derivative with respect to position (d/dx).
- 🔢 The expectation value of an operator, such as momentum or energy, is calculated by integrating the product of the wave function and the operator applied to the wave function over all possible positions.
- 🌀 The Heisenberg uncertainty principle is derived from the non-commutativity of position (x) and momentum (p) operators, leading to the conclusion that these quantities cannot be precisely measured simultaneously.
- 📌 Eigenfunctions and eigenvalues are special functions and numbers associated with linear operators, where the action of the operator on the eigenfunction results in a scaled version of the eigenfunction, with the scaling factor being the eigenvalue.
- 🛠️ The Schrodinger equation, a fundamental equation in quantum mechanics, describes how the wave function of a quantum system evolves over time and is derived from the energy operator acting on the wave function.
- 🔄 The time evolution of a quantum system is deterministic, given the initial wave function; the system's wave function at any later time can be calculated using the Schrodinger equation.
- 🔢 The Schrodinger equation is a first-order differential equation in time and a second-order differential equation in space, requiring complex numbers and being linear and deterministic.
Q & A
What is the significance of the Schrodinger equation in quantum mechanics?
-The Schrodinger equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time. It is used to calculate the wave function of a system, which provides information about the probabilities of finding a particle in particular states.
What are the two main properties of wave functions according to the transcript?
-The two main properties of wave functions are that they are continuous and normalizable. This means that wave functions must be smooth and finite in extent, allowing for the calculation of probabilities.
How is the probability associated with a particle's position described?
-The probability associated with a particle's position is described by the square of the wave function (psi) evaluated at a particular position x. This is because the probability density is given by |psi(x)|^2.
What is the concept of superposition in quantum mechanics?
-Superposition in quantum mechanics refers to the idea that a quantum system can be in a combination of multiple states simultaneously. A wave function can be a superposition of different eigenfunctions, each corresponding to a possible state of the system.
What is an operator in the context of quantum mechanics?
-In quantum mechanics, an operator is a mathematical object that acts on a wave function to produce another function. It is used to represent physical quantities such as momentum, position, and energy. Operators are crucial for calculating expectation values and for understanding the dynamics of quantum systems.
How does the Heisenberg uncertainty principle relate to the non-commutativity of operators?
-The Heisenberg uncertainty principle states that there is a fundamental limit to the precision with which certain pairs of physical properties, such as position and momentum, can be known simultaneously. This principle is a consequence of the non-commutativity of the corresponding operators, which means that the order in which they are applied to a wave function matters.
What is the role of eigenfunctions and eigenvalues in quantum mechanics?
-Eigenfunctions and eigenvalues play a crucial role in quantum mechanics. Eigenfunctions represent the states in which a system can exist, and eigenvalues correspond to the values of the physical quantities associated with these states. When an operator is applied to its eigenfunction, it returns the eigenfunction multiplied by its eigenvalue, which is a constant. This relationship is essential for solving quantum systems and understanding their behavior.
What does the commutator of two operators represent?
-The commutator of two operators, say X and P, is defined as [X, P] = XP - PX and represents the difference in the result when the order of the operators is changed. In quantum mechanics, non-zero commutators indicate that the operators do not commute, which is a key concept in the Heisenberg uncertainty principle.
What is the significance of the Dirac delta function in quantum mechanics?
-The Dirac delta function is a mathematical construct used in quantum mechanics to represent a state where a particle is localized at a specific point. It is not a physical wave function because it is not normalizable, but it is extremely useful in calculations involving point measurements and in the mathematical formalism of quantum mechanics.
How does the expectation value of an operator relate to the physical properties of a quantum system?
-The expectation value of an operator is a fundamental concept in quantum mechanics that gives the average or mean value of a physical quantity for a given quantum state. It is calculated by taking the inner product of the wave function with the operator acting on it, and then integrating over all space. This value provides insight into the probable outcomes of measurements on the system.
What is the role of linear operators in quantum mechanics?
-Linear operators are those that satisfy the property of superposition, meaning that the action of the operator on a linear combination of functions is the same as the linear combination of the actions of the operator on each function individually. This property is crucial in quantum mechanics because it allows for the straightforward application of the superposition principle, which is a fundamental aspect of quantum states.
Outlines
📚 Introduction to Quantum Mechanics and Operators
The paragraph introduces the basics of quantum mechanics, focusing on the role of wave functions and operators in describing the behavior of particles. It discusses the concept of continuity and normalizability of wave functions, the association of probability with wave functions, and the principle of superposition. The lecture also touches on the relationship between operators and physical observables, such as momentum and position, and introduces the idea of eigenfunctions and eigenvalues.
🕒 Time Evolution and Wave Functions
This section delves into the time-dependent aspect of quantum mechanics, explaining how the wave function of a particle evolves over time. It establishes the connection between the wave function and the particle's momentum and energy, and introduces the concept of the energy operator. The discussion also leads to the formulation of the Schrödinger equation, which describes how the wave function changes with time, and emphasizes the importance of this equation in the study of quantum mechanics.
🌀 Commutation and Uncertainty Principles
The paragraph discusses the commutation relations between operators, particularly focusing on the non-commutability of the position and momentum operators. It explains the concept of the commutator and its significance in understanding the uncertainty principle. The lecture highlights the mathematical relationship that underlies the incompatibility of simultaneous measurements of position and momentum, and how this is reflected in the wave function's collapse upon measurement.
🔄 Eigenfunctions and Quantum Postulates
This section explores the properties of eigenfunctions and their role in quantum mechanics. It explains how any wave function can be expanded as a superposition of eigenfunctions and how the coefficients of this expansion relate to the probabilities of measuring certain values for physical observables. The lecture also presents the postulates that govern the measurement process and the collapse of the wave function, emphasizing the strange and counterintuitive nature of quantum mechanics.
🌟 The Schrödinger Equation and Time Evolution
The paragraph concludes the lecture by discussing the Schrödinger equation, which describes the time evolution of quantum systems. It explains the conceptual leap from a simple equation for particles with definite energy to the full Schrödinger equation, which incorporates the energy operator. The lecture highlights the equation's requirements for complex numbers, its linearity, and its deterministic nature, and emphasizes the central role of the Schrödinger equation in quantum mechanics.
Mindmap
Keywords
💡Wave Functions
💡Schrodinger Equation
💡Probability
💡Superposition
💡Operators
💡Eigenfunctions and Eigenvalues
💡Linearity
💡Heisenberg Uncertainty Principle
💡Quantum States
💡Expectation Value
💡Unitary Time Evolution
Highlights
The Schrodinger equation is introduced, which is fundamental to quantum mechanics.
Wave functions are complex numbers and have properties of being continuous and normalizable.
The probability associated with a particle is given by the square of the wave function.
Superposition of allowed states is a key concept, where particles can exist in multiple states simultaneously.
The momentum of a particle is related to the operator acting on the wave function, represented as ħ over i times the derivative with respect to x.
The expectation value of an operator is computed using the integral of the operator acting on the wave function and the conjugate of the wave function.
Eigenfunctions and eigenvalues are special functions and values associated with linear operators, where the operator acting on the eigenfunction returns a scaled version of the eigenfunction.
The commutator of position (x) and momentum (p) operators is iħ, a fundamental result in quantum mechanics indicating non-commutativity.
Upon measurement of an observable, the wave function collapses to the corresponding eigenfunction of the measured value.
The Heisenberg uncertainty principle is derived from the non-commutativity of position and momentum operators.
Arbitrary wave functions can be expanded as a superposition of eigenfunctions of an operator.
The probability of measuring a specific eigenvalue is given by the square of the corresponding coefficient in the superposition.
The time evolution of a wave function is governed by the Schrodinger equation, which is a first-order differential equation in time and second-order in space.
The Schrodinger equation requires complex numbers, is linear, and deterministic, allowing for the prediction of wave functions at any future time given the initial condition.
The energy operator is related to the second derivative of the wave function with respect to time.
De Broglie proposed that particles can be described by waves, leading to the concept of matter waves.
The historical development of quantum mechanics is discussed, including the contributions of Planck, Einstein, Compton, and De Broglie.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: