Electric Flux

Flipping Physics
23 Jan 202310:04
EducationalLearning
32 Likes 10 Comments

TLDRThe video explains the concept of electric flux, defined as the amount of electric field passing through a surface. Using examples, it demonstrates calculating electric flux for a right triangular box in a uniform electric field. The key points include the formula for electric flux, the direction of area vectors, and how the angle between the electric field and area affects flux calculations. The lesson concludes with understanding that the net electric flux through a closed surface can sum to zero, depending on the field directions through the surface.

Takeaways
  • 🔋 The term 'flux' refers to an effect that appears to pass through a surface or substance, not necessarily moving.
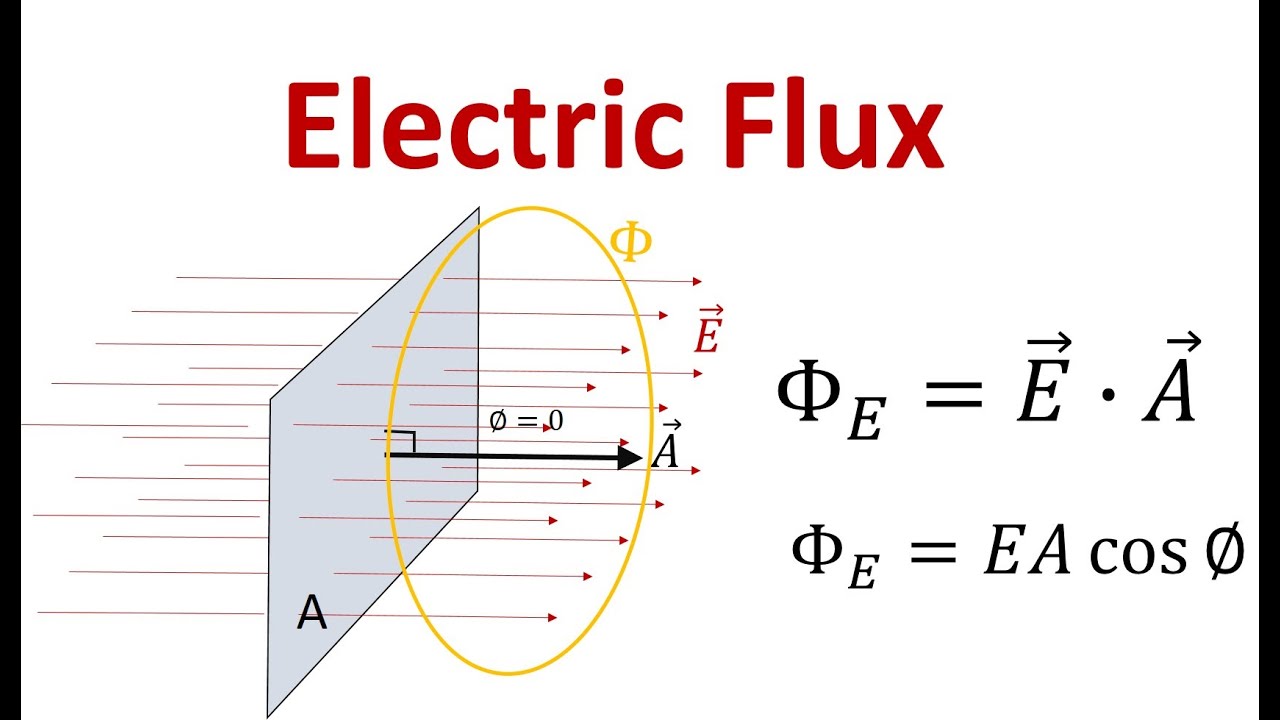
  • 📏 Electric flux is symbolized by uppercase Phi (Φ) and measures the amount of electric field passing through a defined area.
  • 📚 The formula for electric flux through a uniform electric field is Φ_E = E • A, where E is the electric field, A is the area, and the dot product represents the cosine of the angle between them.
  • 📐 The direction of an area vector is always normal to the plane of the area, similar to the direction of angular velocity in rotation.
  • ⚡ The units for electric flux are newtons times square meters per coulomb, derived from the units of electric field and area.
  • 📦 To determine the net electric flux through a closed surface, like a right triangular box, calculate the flux through each side and sum them.
  • 🔍 The electric flux through the bottom of the box is zero because the electric field is perpendicular to the surface.
  • 📏 For the triangular sides, no flux passes through because the electric field is parallel to the surfaces, resulting in zero flux.
  • 📐 The top surface of the box has an electric flux that can be calculated using the geometry of the triangle and the electric field's direction.
  • 🔄 The net electric flux through a closed surface, in this case, the right triangular box, sums to zero, reflecting the conservation of electric charge.
  • 🍵 The script includes a humorous anecdote about learning language nuances and a light-hearted moment involving tea, adding a personal touch to the educational content.
Q & A

  • What is the term 'flux' defined as in the context of physics?

    -Flux is defined as any effect that appears to pass or travel through a surface or substance, without the actual need for the effect to move.

  • What is the symbol used for electric flux?

    -The symbol for electric flux is an uppercase Phi (Φ) with a subscript capital E (Φ_E).

  • How is electric flux related to the electric field and the area through which it passes?

    -Electric flux is the measure of the amount of electric field that passes through a defined area and is calculated as the dot product of the electric field vector and the area vector, or as the product of the electric field, area, and the cosine of the angle between them.

  • What is the direction of the area vector in the context of electric flux?

    -The direction of the area vector is always normal to the plane of the area, similar to the direction of angular velocity being normal to the plane of rotation.

  • How is the equation for electric flux similar to the work equation for a constant force?

    -The equation for electric flux has the same form as the work equation, where work equals the dot product of force and displacement, or force times displacement times the cosine of the angle between the force and displacement vectors.

  • What determines if the electric flux is positive or negative?

    -The value of the cosine of the angle between the electric field and the area determines if the electric flux is positive (when the field is coming out of the surface) or negative (when the field is going into the surface).

  • What are the units for electric flux?

    -The units for electric flux are newtons times square meters divided by coulombs (N·m²/C), derived from the units of electric field (newtons per coulomb) and area (square meters).

  • How is the net electric flux determined for a closed surface, such as the right triangular box in the example?

    -The net electric flux through a closed surface is determined by calculating the electric flux through all sides of the surface and then summing these fluxes.

  • Why is the electric flux through the bottom surface of the right triangular box zero?

    -The electric flux through the bottom surface is zero because the electric field lines are parallel to the bottom surface, meaning none of the field lines pass through it, resulting in a 90-degree angle and a cosine value of zero.

  • What is the significance of the angle between the area vector and the electric field in calculating electric flux?

    -The angle between the area vector and the electric field is crucial as it affects the cosine value used in the electric flux calculation, which in turn determines the magnitude and sign (positive or negative) of the flux.

  • What is the net electric flux through the closed right triangular box in the example, and why?

    -The net electric flux through the closed right triangular box is zero because the sum of the electric fluxes entering and exiting the box through different surfaces cancels each other out.

Outlines
00:00
🔋 Understanding Electric Flux

This paragraph introduces the concept of 'flux' as an effect that appears to pass through a surface without necessarily moving. It specifically discusses 'electric flux', symbolized by uppercase Phi with a subscript E, which measures the amount of electric field passing through a defined area. The formula for calculating electric flux in a uniform field is given, highlighting the dot product relationship between the electric field vector and the area vector, including the cosine of the angle between them. The paragraph also compares this to the work done by a constant force and clarifies that electric flux is a scalar quantity with units of newtons times square meters per coulomb. An example of calculating the net electric flux through a right triangular box in a uniform electric field is introduced.

05:04
📐 Calculating Electric Flux Through a Triangular Box

The second paragraph delves into the process of calculating the electric flux through each of the five sides of a right triangular box within a uniform electric field. It explains how to determine the flux through the back side (area 1) by considering the angle between the electric field and the area vector, which results in a negative flux due to the 180-degree angle. The bottom side (area 2) is shown to have zero flux because the electric field is perpendicular to this surface. The triangular sides (areas 3 and 4) also have zero flux as the electric field lines do not penetrate these surfaces. The top surface (area 5) requires geometric understanding to determine the angle between the electric field and the area vector, leading to a positive flux calculation. The net electric flux through the closed surface of the box is then discussed, revealing that it sums to zero, which is a key concept in understanding the conservation of electric flux.

Mindmap
Keywords
💡Flux
Flux refers to the concept of an effect that appears to pass through a surface or substance without necessarily moving. In the context of the video, it is central to understanding how different forms of energy or fields interact with defined areas. The script uses the term to introduce the concept of electric flux, which is a measure of the electric field passing through a surface.
💡Electric Flux
Electric flux is a specific type of flux that deals with electric fields. It is symbolized by the uppercase Phi (Φ) with a subscript E. The script explains that electric flux is calculated using the dot product of the electric field and the area through which it passes, emphasizing its importance in gauging the amount of electric field lines penetrating a given area.
💡Dot Product
The dot product is a mathematical operation that takes two vectors and returns a scalar. In the script, it is used to calculate electric flux, representing the component of the electric field that is perpendicular to the surface area, which is crucial for determining the flux through that area.
💡Uniform Electric Field
A uniform electric field is an electric field where the field strength and direction are constant throughout the space. The video script discusses how electric flux is calculated in such a field, highlighting its uniformity as a simplifying factor in the calculations.
💡Area Vector
An area vector is a vector that is perpendicular to the surface of an area, indicating direction as well as magnitude. The script explains that the direction of an area vector is always normal to the plane of the area, which is essential when calculating the electric flux through that area.
💡Cosine
The cosine function is a trigonometric function that relates the angle between two vectors to their dot product. In the context of the video, cosine is used to determine the component of the electric field that contributes to the flux through a surface, as it depends on the angle between the electric field and the area vector.
💡Scalar
A scalar is a quantity that has magnitude but no direction. The script mentions that electric flux is a scalar, meaning it only has a size and does not have a direction associated with it, which is important for understanding how it is summed in calculations.
💡Newtons per Coulomb
Newtons per Coulomb is the unit of electric field strength. The script explains that when calculating electric flux, the electric field's strength is measured in this unit, which is essential for understanding the units of electric flux.
💡Closed Surface
A closed surface is a surface that completely encloses a volume with no gaps. The script discusses determining electric flux through a closed surface, such as a right triangular box, which is important for understanding the net electric flux in a contained space.
💡Net Electric Flux
Net electric flux is the total electric flux through a closed surface, taking into account all contributions from different parts of the surface. The script uses the example of a right triangular box to illustrate how to calculate the net electric flux by summing the fluxes through each side.
💡Right Triangular Box
A right triangular box is a three-dimensional shape with a triangular base and rectangular sides. The script uses this shape as an example to demonstrate the calculation of electric flux through different surfaces, emphasizing the geometrical aspects of the problem.
Highlights

Flux is defined as any effect that appears to pass or travel through a surface or substance, without necessarily moving.

Electric flux is measured by the amount of electric field passing through a defined area.

The equation for electric flux of a uniform electric field is Φ_E = E • A * cos(θ), where E and A are vectors.

The direction of an area is always normal to the plane of the area, similar to angular velocity.

Electric flux has the same mathematical form as work done by a constant force.

Electric flux is a scalar quantity, with units of newtons times square meters per coulomb.

Net electric flux is determined through a closed surface by summing the flux through all sides.

The plural of 'flux' is 'fluxes', not 'flux'.

The direction of the area vector for a closed surface is always outward.

There is zero electric flux through the bottom surface of the right triangular box as the electric field lines are parallel.

No electric field lines pass through the triangular sides of the box, resulting in zero flux through these surfaces.

The electric flux through the top surface of the box is calculated using geometry and trigonometry.

The net flux through the closed right triangular box equals the sum of fluxes through all five sides, which is zero.

Electric flux is negative when the electric field is entering a closed surface and positive when exiting.

Learning about electric flux helps in understanding the behavior of electric fields and their interaction with surfaces.

Transcripts

Browse More Related Video

Electric Flux (part 1)

The Electric Flux and It's Applications

Electric flux meaning (& how to calculate it) | Electrostatics | Physics | Khan Academy

Electric Flux and Gauss’s Law | Electronics Basics #6

Electric Flux and Gauss' Law - Review for AP Physics C: Electricity and Magnetism

Gauss law of electricity | Electrostatics | Physics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Electric FluxPhysics EducationFlux CalculationTriangular BoxElectric FieldClosed SurfaceVector AnalysisEducational ContentLearning ToolScience Tutorial