Electric Flux Paradox
TLDRThis script explores the paradox of infinite electric charge density in space, challenging our understanding of electric flux and fields. It explains how electric flux is generated and absorbed, and its implications for the strength and direction of electric fields. The paradox arises when considering an infinite, uniformly charged space, where the electric field strength would theoretically increase to infinity, contradicting our intuition. The script suggests that a better theory of electromagnetism might be needed to resolve this issue, contrasting it with the gravitational flux paradox resolved by General Relativity. It concludes by questioning the physical possibility of such a universe, hinting at the need for further exploration.
Takeaways
- 🌌 The concept of an infinite space filled with infinite electric charge leads to paradoxes in understanding electric fields.
- 🔋 Electric flux is a mathematical construct that helps calculate the behavior of charged particles, representing the strength and direction of the electric field.
- 🧲 The density of electric flux is greatest near charged particles, indicating the strongest electric fields, but it's continuous and not an actual flow.
- 🤔 The electric field strength increases with the distance from the center in an infinite charged space, contradicting our intuition that it should remain constant or decrease.
- 🔄 Particles with the same charge repel, while opposite charges attract, influencing the distribution and behavior of charges in space.
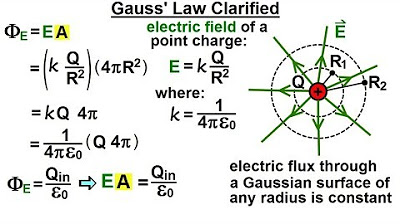
- 📐 The net electric charge inside a closed surface determines the net electric flux through it, regardless of the surface's size or shape.
- 💡 The scenario of uniform positive charge density throughout space results in an infinite electric field strength at infinity, which is a contradiction.
- 🌐 In a closed universe, a uniform charge density has no mathematical solution unless the total positive and negative charges are exactly equal.
- 🌈 For an infinite universe, an infinite amount of charge is possible without contradictions, unlike in a closed universe.
- 🤷♂️ The paradox of infinite charge density in space has not been resolved and suggests a need for a better theory of electromagnetism.
- ⚛️ Unlike electromagnetism, general relativity handles uniform mass density without paradoxes, hinting at a possible resolution for electromagnetism as well.
- 🚫 The universe may not be able to have a net charge density throughout all space, making the paradox of an infinite charged space a moot point.
Q & A
What is electric flux and why is it significant in understanding the paradox of infinite electric charge?
-Electric flux is a measure of the electric field that passes through a given surface. It is significant in understanding the paradox of infinite electric charge because it helps to illustrate the concept of how an electric field behaves in space, especially when considering a scenario with an infinite distribution of charge.
How does the density of electric flux relate to the strength of the electric field?
-The density of electric flux is largest near charged particles, indicating that the electric field is strongest in these areas. The amount of flux is a direct indication of the electric field's strength.
Why is electric flux considered a mathematical concept rather than a physical entity?
-Electric flux is considered a mathematical concept because it is a tool used to calculate the behavior of charged particles. It does not physically exist or flow; instead, it provides a way to understand and quantify the influence of electric fields.
What is the relationship between the electric flux passing through a surface and the electric field?
-The electric flux passing through a surface depends on the strength of the electric field, the area of the surface, and the angle the surface makes with the electric field. It quantifies the total electric field influence on that surface.
How does the concept of electric charge affect the behavior of particles with the same or opposite charges?
-Particles with the same charge repel each other, while particles with opposite charges attract each other. This interaction is a fundamental principle of electromagnetism that dictates how charged particles will behave in relation to one another.
What is the Gauss's Law and how does it relate to the concept of electric flux in a closed surface?
-Gauss's Law states that the net amount of electric flux entering or exiting a closed surface is equal to the net amount of electric charge enclosed, divided by the permittivity of free space. It is directly related to electric flux as it quantifies the relationship between enclosed charge and the flux through a boundary.
What contradictions arise when considering an infinite space with a uniform positive charge density?
-The contradictions include the logical inconsistency that as the volume of a closed surface grows, the electric field strength should increase without bound, which contradicts the physical expectation that the field should diminish with distance. Additionally, having an infinite number of mathematical solutions for the electric field in such a space leads to contradictions among these solutions.
How does the concept of a Closed Universe affect the possibility of a uniform charge density?
-In a Closed Universe, where space-time wraps around itself, a uniform charge density would have no mathematical solution. For a logically consistent solution, the total amount of positive charge must be exactly equal to the total amount of negative charge, with no extra particles allowed.
What is the difference between the paradox of infinite electric charge and the analogous paradox in Newton's Theory of Gravity?
-The paradox of infinite electric charge arises due to the possibility of having an infinite number of mathematical solutions for the electric field in an infinite space with uniform charge density. In contrast, Newton's Theory of Gravity has a similar paradox with gravitational flux in an infinite space with uniform mass density, but this paradox is resolved in Einstein's General Relativity, which can handle a uniform mass density without issues.
Why might a better theory of electromagnetism be needed to resolve the paradox of infinite charge density?
-A better theory of electromagnetism might be needed because the current understanding struggles with the concept of a uniform charge density throughout all space, leading to paradoxical results. This suggests that our current models may be incomplete or limited in their applicability to such extreme scenarios.
What is the fundamental difference between electric charges and gravitational masses in terms of their ability to cancel each other out?
-Electric charges can cancel each other out due to the existence of both positive and negative charges. However, gravitational masses cannot cancel each other out because all masses contribute positively to the gravitational field, and there are no negative masses in the universe as far as we know.
Outlines
🔋 The Paradox of Infinite Electric Charge
This paragraph delves into the paradoxical implications of an infinite space filled with infinite electric charge. It introduces the concept of electric flux, which is generated by positive charges and absorbed by negative ones, highlighting its density near charged particles and its role in indicating the electric field's strength and direction. The script points out that electric flux is a mathematical construct rather than a physical entity. It discusses the behavior of charged particles, including repulsion and attraction based on charge similarity and distance. The paradox arises when considering a uniform positive charge density throughout space, leading to an infinite increase in the electric field's strength as distance from any point increases to infinity. This scenario results in multiple contradictory mathematical solutions, challenging our understanding of electric fields in an infinite space.
🌌 The Infinite Charge Paradox and Boundary Conditions
The second paragraph explores the complexity of defining the electric field in an infinite space with uniform charge density. It begins by stating that without boundary conditions, such as the electric field's value at a specific point, there are infinite mathematical solutions for the electric field, drawing an analogy with Newton's Laws of Motion. The script then addresses the paradox that arises when trying to reconcile the intuitive expectation of a net-zero electric field due to symmetry with the mathematical solutions indicating an infinite increase in field strength. It contrasts this with scenarios in a closed universe, where the only consistent solution would be an exact balance of positive and negative charges, and an infinite universe, where an imbalance is permissible. The paragraph also touches on the resolution of similar gravitational paradoxes in General Relativity, suggesting that a new theory of electromagnetism might be needed to address the uniform charge density paradox. It concludes by considering the possibility that a universe with a net charge density throughout space may be physically impossible, which would render the paradox moot.
Mindmap
Keywords
💡Infinite space
💡Electric flux
💡Electric field
💡Charged particles
💡Electric charge density
💡Closed surface
💡Gauss's law
💡Paradox
💡Newton's Laws of motion
💡General Relativity
💡Boundary condition
Highlights
An infinite space of infinite electric charge leads to a paradox with profound implications.
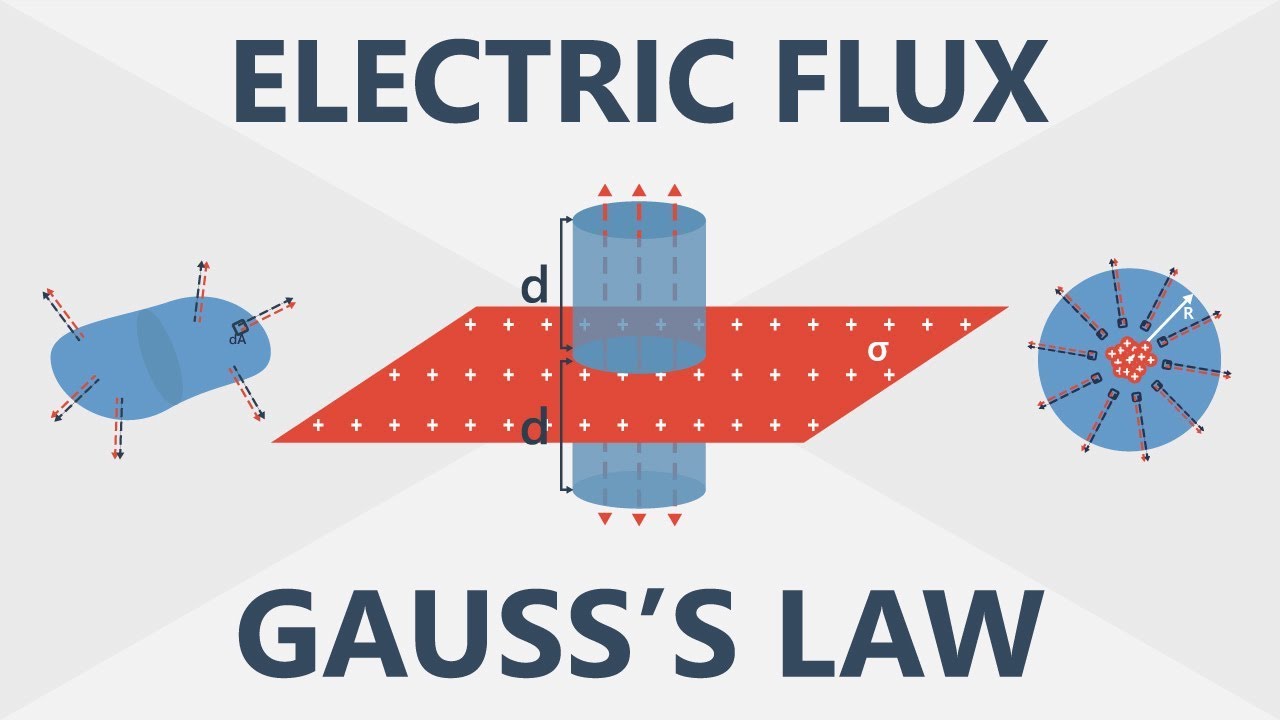
Electric flux is generated by positively charged particles and absorbed by negatively charged ones.
The density of electric flux indicates the strength of the electric field.
Electric flux is a continuous concept in space, despite not physically existing as a flow.
Electric flux is a mathematical concept for calculating the behavior of charged particles.
Like charges repel, opposite charges attract, with proximity affecting the strength of interaction.
Electric flux passing through a surface depends on the electric field strength, surface area, and angle.
A closed surface's net electric flux is determined by the enclosed charge, regardless of its size or shape.
Opposite charges cancel out, leading to equal electric flux entering and exiting a closed surface.
Uniform positive charge density in infinite space results in a net flux exiting every closed surface.
As volume grows, the electric field strength theoretically increases to infinity, leading to contradictions.
An infinite number of mathematical solutions exist for an infinite space without charged particles.
A boundary condition, such as the electric field at one point, is necessary for a unique solution.
Intuitively, a continuous charge density should result in a net electric field of zero, contradicting mathematical solutions.
A Closed Universe with uniform charge density has no mathematical solution for the electric field.
In a Closed Universe, total positive and negative charges must be equal for a logically consistent solution.
An Infinite Universe can accommodate an infinite amount of extra positive or negative particles.
Solutions exist for infinite lines or planes of charge without paradoxes.
The infinite space of charge paradox remains unresolved, suggesting a need for a better theory of electromagnetism.
General Relativity handles uniform mass density without issues, unlike Newton's Theory of Gravity.
The lack of negative masses in gravity contrasts with the ability of electric charges to cancel each other out.
The Universe must have a positive mass density but not necessarily a positive charge density.
The paradox may indicate that a Universe with a net charge density throughout all space is not physically possible.
Transcripts
Browse More Related Video
Physics 37.1 Gauss's Law Understood (4 of 29) Gauss' Law Clarified

Physics 37.1 Gauss's Law Understood (3 of 29) What is Gauss' Law?

Gauss Law Problems - Infinite Sheet of Charge and Parallel Plate Capacitor - Physics

Electric Flux and Gauss' Law - Review for AP Physics C: Electricity and Magnetism
Electric Flux and Gauss’s Law | Electronics Basics #6

Electric flux meaning (& how to calculate it) | Electrostatics | Physics | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: