Physics 37.1 Gauss's Law Understood (5 of 29) How to Use Gauss' Law

Michel van Biezen
15 Feb 201809:03
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial demonstrates the application of Gauss's law using a simple example involving a point charge of 10 microcoulombs. It explains how to calculate the electric field at different distances by drawing Gaussian surfaces and applying the law to find the field strength at each location. The process involves using the permittivity of free space and the concept of electric flux, ultimately showing how to determine the electric field for various geometric shapes and charge distributions.

Takeaways
  • 📚 Gauss's law is introduced as a method to calculate the electric field around a point charge.
  • 🔍 The example uses a simplistic scenario involving a point charge of 10 microcoulombs to demonstrate the application of Gauss's law.
  • 📏 Three different distances (r1=2m, r2=4m, r3=6m) are considered to find the electric field strength at those locations.
  • 🌐 A Gaussian surface, specifically a sphere, is drawn around the point charge to calculate the electric field at various points.
  • 📍 The charge must be at the center of the Gaussian surface, and the surface edge should be at the point where the electric field strength is to be determined.
  • ⚖️ Gauss's law states that the total electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space (ε₀).
  • 📈 The electric field (E) is assumed to be constant over the surface and perpendicular to it, simplifying the calculation.
  • 🔢 The formula E = Q / (4πr²ε₀) is derived from Gauss's law, where Q is the charge, r is the radius, and ε₀ is the permittivity of free space.
  • 🔄 The constant K from Coulomb's law (1/4πε₀) is used to simplify the expression to E = KQ / r².
  • 📉 As the distance from the charge increases (r2 and r3), the electric field strength decreases, calculated using the derived formula.
  • 🛠 Gauss's law is a powerful tool for finding electric fields for various geometric shapes and charge distributions, with applications shown in future videos.
Q & A

  • What is Gauss's law and why is it used in physics?

    -Gauss's law, also known as Gauss's flux theorem, states that the total electric flux through a closed surface is proportional to the total charge enclosed within the surface. It is used in physics to calculate the electric field due to a charge distribution and simplifies the calculation of electric fields in various geometrical configurations.

  • What is a Gaussian surface and why is it important in applying Gauss's law?

    -A Gaussian surface is an imaginary closed surface used in the application of Gauss's law. It is important because it helps in determining the electric flux through the surface, which is directly proportional to the charge enclosed by the surface. The shape and position of the Gaussian surface can simplify the calculation of electric fields.

  • What is the significance of the point charge in the context of the video script?

    -In the script, a point charge is used as an example to demonstrate the application of Gauss's law. A point charge is a theoretical construct where the charge is assumed to be concentrated at a single point, making it easier to visualize and calculate the electric field at different locations around it.

  • What are the three different locations mentioned in the script for calculating the electric field?

    -The script mentions three different locations at distances of two meters (r1), four meters (r2), and six meters (r3) away from the point charge where the electric field strength needs to be determined.

  • What is the charge enclosed by the Gaussian surface in the example provided?

    -The charge enclosed by the Gaussian surface in the example is a point charge of ten microcoulombs.

  • What is the permittivity of free space denoted by 'epsilon sub naught'?

    -The permittivity of free space, denoted by 'epsilon sub naught' (ε₀), is a physical constant that is used to calculate the electric field in a vacuum. Its value is approximately 8.85 × 10^-12 farads per meter (F/m).

  • How is the electric field strength calculated at each location using Gauss's law?

    -The electric field strength at each location is calculated by dividing the charge enclosed by the Gaussian surface by the permittivity of free space (ε₀) and the surface area of the sphere (4πr²), where r is the distance from the charge to the point of interest.

  • What is the constant K in Coulomb's law and how is it related to the permittivity of free space?

    -The constant K in Coulomb's law is equal to 1/(4πε₀), where ε₀ is the permittivity of free space. It is used to relate the force between two point charges to the product of their charges and the inverse square of the distance between them.

  • What is the electric field strength at r1, r2, and r3 in Newtons per Coulomb?

    -The electric field strength at r1 is approximately 22,500 N/C, at r2 is 5,625 N/C, and at r3 is 2,500 N/C.

  • How does the size of the Gaussian surface affect the calculation of the electric field strength?

    -The size of the Gaussian surface affects the calculation by determining the surface area through which the electric flux is calculated. A larger surface area will result in a smaller electric field strength for the same charge distribution, as the flux is spread over a larger area.

Outlines
00:00
🔋 Introduction to Gauss's Law for Electric Field Calculation

This paragraph introduces Gauss's law as a method for calculating the electric field around a point charge. It uses a simple example of a 10 microcoulombs charge to demonstrate the process. The electric field is to be determined at three different distances (r1, r2, and r3) from the charge. The concept of a Gaussian surface, in this case, a sphere, is introduced as a tool to apply Gauss's law. The importance of the charge being at the center of the sphere and the surface reaching the points of interest for electric field strength is emphasized.

05:03
📏 Applying Gauss's Law to Calculate Electric Field Strengths

The second paragraph delves into the application of Gauss's law to find the electric field strength at the specified distances from the point charge. It explains the use of the integral form of Gauss's law, assuming a constant electric field along the surface and perpendicularity to it. The calculation involves the charge enclosed, the surface area of the Gaussian sphere, and the permittivity of free space (epsilon sub naught). The paragraph provides detailed steps for calculating the electric field strength (E1) at the first location using the formula E = Q / (4πr²ε₀), where Q is the charge, r is the radius, and ε₀ is the permittivity of free space. It also mentions the use of Coulomb's constant (K) for simplification. The process is then generalized for finding the electric field strengths at the other two locations (E2 and E3) by adjusting the radius of the Gaussian surface accordingly.

Mindmap
Keywords
💡Gauss's Law
Gauss's Law, also known as the Gauss's flux theorem, is a fundamental principle in electromagnetism that relates the electric flux through a closed surface to the electric charge enclosed by the surface. In the video, Gauss's Law is used to calculate the electric field around a point charge. The law states that the total electric flux through a closed surface is proportional to the charge enclosed by the surface. The script demonstrates how to apply Gauss's Law by using a Gaussian surface, typically a sphere in this context, to find the electric field at various distances from the charge.
💡Point Charge
A point charge refers to an electric charge that is concentrated at a single point in space. In the video, the concept of a point charge is central to the example given, where a point charge of ten microcoulombs is used to illustrate the application of Gauss's Law. The point charge is assumed to be at the center of the Gaussian surface, simplifying the calculations by ensuring that the electric field is radially symmetric around the charge.
💡Electric Field
The electric field is a vector field that surrounds electric charges and exerts a force on other charges in its vicinity. The strength and direction of the electric field are what Gauss's Law is used to determine in the script. The video explains how to calculate the electric field strength at three different locations relative to a point charge, demonstrating the application of the law in practical scenarios.
💡Gaussian Surface
A Gaussian surface is an imaginary surface used in the application of Gauss's Law to calculate electric fields. In the video, the Gaussian surface is described as a sphere centered on the point charge, with its edge located at the point where the electric field strength is to be determined. The script emphasizes the importance of the Gaussian surface's shape and position for the accurate calculation of the electric field.
💡Flux
Flux, in the context of electromagnetism, refers to the quantity of a field, such as the electric field, passing through a given surface. The video script explains that the flux through the Gaussian surface is the same everywhere, which is a key assumption in applying Gauss's Law. The flux is used to calculate the electric field strength at various points around the point charge.
💡Permittivity of Free Space
The permittivity of free space, denoted as epsilon sub naught in the script, is a physical constant that relates the electric field to the electric displacement field in a vacuum. It is used in the formula for Gauss's Law to calculate the electric field. The script mentions this constant in the context of the formula for electric field strength around a point charge.
💡Coulomb's Law
Coulomb's Law describes the force between two point charges and is related to Gauss's Law through the constant K, which is the product of 1/4π and the permittivity of free space. In the video, Coulomb's Law is indirectly referenced when the script simplifies the calculation of the electric field by replacing 1/4πε₀ with K, making the formula more recognizable and easier to apply.
💡Integral Format
The integral format mentioned in the script refers to a mathematical representation of Gauss's Law using integral calculus. It is used to express the law in a form that is suitable for calculating the electric field when the field is constant over a surface, such as the Gaussian surface in the video's example.
💡Surface Area
The surface area of the Gaussian surface is crucial in the calculation of the electric field. The script explains that the electric field strength is inversely proportional to the square of the radius of the Gaussian surface, which is why the surface area (4πr²) is used in the denominator of the formula for electric field strength.
💡Newton's Per Coulomb
Newton's per Coulomb is the unit of electric field strength, indicating the force experienced by a unit positive charge in an electric field. In the video, the script calculates the electric field strength in Newtons per Coulomb, providing a measure of the force that would be experienced by a charge placed in the field at the specified locations.
Highlights

Introduction to using Gauss's law with a simple example to demonstrate the concept.

Using Gauss's law to find the electric field strength at different locations around a point charge.

Explanation of why Gauss's law is used, even for simple scenarios.

Setting up a Gaussian surface as a sphere centered on the point charge to find the electric field.

Ensuring the charge is at the center of the sphere and the surface edge is at the point of interest.

Using Gauss's law to calculate the electric field strength (E1) at a distance (r1) from the charge.

Flux through the surface is the same everywhere, leading to the equation E = Q/ε₀A.

Simplifying the equation by assuming a constant electric field perpendicular to the surface.

Calculating E1 using the formula E = Q/(4πε₀R₁²).

Using Coulomb's constant (K) to simplify the calculation of electric field strength.

Finding the electric field strength at different distances (E2 and E3) by adjusting the Gaussian surface size.

General formula for electric field strength using Gauss's law: E = KQ/R².

Practical application of Gauss's law for various geometric shapes and charge distributions.

Gauss's law simplifies the process of finding electric fields in complex scenarios.

The importance of correctly positioning the Gaussian surface to accurately determine electric field strength.

Demonstration of how changing the size of the Gaussian surface allows for finding electric fields at different points.

Transcripts

Browse More Related Video

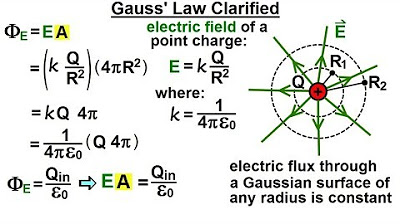
Physics 37.1 Gauss's Law Understood (4 of 29) Gauss' Law Clarified

Electric Flux and Gauss’s Law | Electronics Basics #6

Electric Flux and Gauss' Law - Review for AP Physics C: Electricity and Magnetism

4. Gauss's Law and Application to Conductors and Insulators

Gauss law of electricity | Electrostatics | Physics | Khan Academy

Ultimate Gauss' Law review

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Gauss's LawElectric FieldPoint ChargePhysics TutorialEducational ContentElectrostaticsMathematical ExampleScience LearningElectric FluxPermittivity