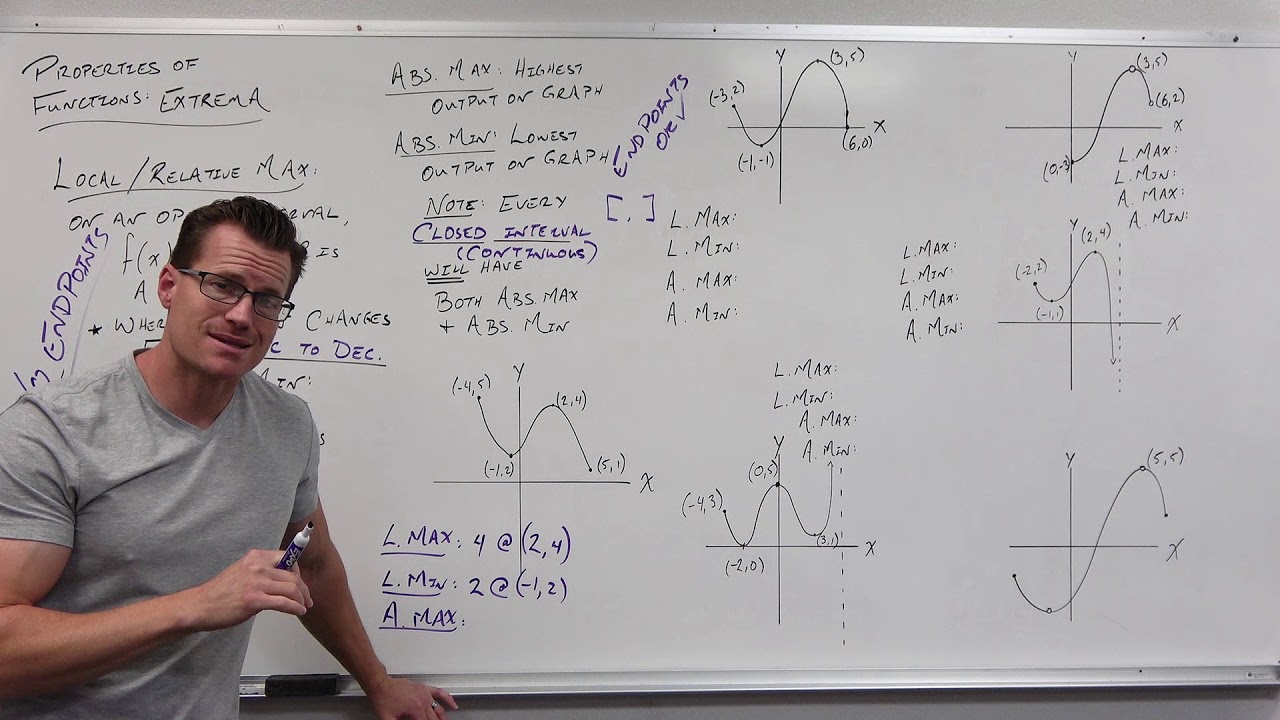
BusCalc 19 Local and Global Extrema
TLDRThis video script delves into the concepts of local and global extrema, focusing on the identification of minimums and maximums on a curve. Local extrema are defined as points where the function's value is the highest or lowest within a small neighborhood, while global extrema represent the absolute highest or lowest value of the function across its entire domain. The importance of critical points is highlighted, as local extrema must occur at these points where the first derivative is zero. The video also discusses the role of the second derivative in determining whether a critical point is a local minimum or maximum. It clarifies that while local extrema are always at critical points for differentiable functions, non-differentiable points can also represent extrema. The script further explains that global extrema are unique values that can occur at multiple points within the domain. The video provides examples to illustrate these concepts, emphasizing the need to consider the function's domain and differentiability when identifying extrema.
Takeaways
- 📌 Local extrema (minimums and maximums) are points on a curve where the function's value is the highest or lowest within a small neighborhood.
- 📈 A local maximum is a point where the function has the largest value compared to its surrounding points, while a local minimum is where it has the smallest value.
- 🔍 To identify local extrema, one must look for critical points where the first derivative is zero and analyze the slope of the tangent lines.
- 📉 A function that is strictly increasing over its entire domain does not have a local minimum or maximum.
- 🔢 The first derivative being zero at a critical point is a prerequisite for a local extremum, but it must also be accompanied by a positive second derivative for a minimum or a negative second derivative for a maximum.
- ✍️ The second derivative test is used to determine if a critical point is a local minimum (positive) or a local maximum (negative).
- 🌍 Extrema is an umbrella term that includes both local minima and maxima, encompassing all the extreme values of a function.
- 🏔️ A global minimum is the lowest possible value of a function, which might occur at multiple points, while a global maximum is the highest possible value.
- 🌟 Global extrema are synonymous with absolute extrema and are identified by giving the coordinate pair (x, y) of the extreme point.
- ⚠️ It's important to note that local extrema must occur at a critical point for a differentiable function, but non-differentiable points can also be extrema without being critical points.
- 📈 For piecewise functions, one must be cautious to identify the correct intervals where the function is defined to accurately determine local extrema.
Q & A
What is meant by 'extrema' in the context of this video?
-In the context of this video, 'extrema' refers to the highest (maximum) and lowest (minimum) values of a function. It includes both local and global maxima and minima.
How are local extrema defined in terms of a function's behavior?
-Local extrema are defined as points on a function where the value is either the highest (local maximum) or lowest (local minimum) compared to the surrounding points within a small neighborhood of the input values.
What is the relationship between local extrema and critical points?
-Local extrema must occur at critical points, which are points where the first derivative of the function is equal to zero. At these points, the tangent line to the function is horizontal, indicating neither an increase nor a decrease in the function's value.
How can you determine if a critical point is a local minimum or a local maximum using the second derivative?
-If the second derivative is positive at a critical point, it is a local minimum. Conversely, if the second derivative is negative at a critical point, it is a local maximum.
What is the difference between a local maximum and a global maximum?
-A local maximum is the highest value of the function within a local neighborhood, whereas a global maximum is the highest value of the function across its entire domain. There can be multiple local maxima, but only one global maximum.
What is the significance of the first derivative in determining the nature of a critical point?
-The first derivative indicates the slope of the tangent line to the function. If the first derivative is increasing (moving from negative to positive), it indicates a local minimum. If it is decreasing (moving from positive to negative), it indicates a local maximum.
What is the term used to describe the set of all extreme values of a function?
-The term used to describe the set of all extreme values of a function is 'extrema'.
How does the concept of a global minimum differ from a local minimum?
-A global minimum is the lowest possible value of the function across its entire domain, which might occur at multiple points, whereas a local minimum is the lowest value within a small neighborhood of the function's domain.
What is the correct way to answer a question asking for the maximum or minimum of a function?
-The correct way to answer such a question is by providing a coordinate pair, which includes both the x-value (input) and the y-value (output or value of the function) at the point of the extreme.
Can a function have a local maximum or minimum at a point where it is not differentiable?
-Yes, a function can have a local maximum or minimum at a point where it is not differentiable. However, such a point would not be considered a critical point since the derivative does not exist at that point.
Why might a point that appears to be a local minimum not actually be one?
-A point that appears to be a local minimum might not actually be one if the function's domain or the piecewise definition of the function does not include that point. Additionally, if the function's value can be made lower by slightly adjusting the input value, then the point is not a local minimum.
What is a piecewise function and how does it relate to local extrema?
-A piecewise function is a function that is defined by multiple pieces, each with its own formula, often applied over different intervals of the domain. Local extrema within a piecewise function must be evaluated carefully, as the function's behavior and continuity can change at the boundaries between pieces, which can affect the identification of local maxima and minima.
Outlines
📈 Understanding Local and Global Extrema
The video begins by discussing local and global extrema, which are the minimum and maximum values of a function, respectively. It uses a blue curve to illustrate the concepts of local minimum and maximum, explaining that these points are considered extrema within their immediate neighborhood. The video also clarifies that a local maximum can be higher or lower than the global maximum, and vice versa for the minimum. It introduces the concept of critical points, where the first derivative of a function is zero, and explains that local extrema must occur at these points. The video provides a formal definition of local minima and maxima based on the sign of the second derivative, and emphasizes the importance of identifying extrema using coordinate pairs.
🌍 Global Minima and Maxima: The Broad View
The video continues by differentiating between local and global extrema. It explains that a global minimum is the lowest value of the function across its entire domain, which can occur at multiple points, while a global maximum is the highest value. The video also discusses the terminology of extrema, which encompasses all extreme values, including both local and global minima and maxima. It provides an example of a curve with a local maximum but no global maximum, as the function increases indefinitely in both directions. The importance of providing both the x and y values when identifying extrema is highlighted.
📉 Special Cases of Extrema and Non-Differentiability
The video addresses special cases where a function might have a global minimum or maximum that occurs at non-differentiable points. It clarifies that while local extrema of differentiable functions must occur at critical points, this is not the case for non-differentiable points, which can still represent extrema. The video also discusses piecewise functions, noting that local extrema can occur at points of discontinuity, which are not differentiable. It provides an example of a piecewise function with a local maximum at a point of discontinuity, and clarifies that an apparent local minimum may not actually exist if the function's value can be lower elsewhere within the domain.
🔍 Closer Look at Function Pieces and Discontinuities
The final paragraph emphasizes the need to carefully consider the domain and the points where different pieces of a function apply. It cautions against assuming a local minimum exists based solely on the graph's appearance, as the function's definition must be taken into account. The video concludes by reassuring viewers that the explanations provided aim to clarify rather than complicate the understanding of extrema, and looks forward to the next video.
Mindmap
Keywords
💡Local extrema
💡Critical points
💡Second derivative
💡Global extrema
💡Absolute maximum and minimum
💡Differentiable function
💡Piecewise function
💡Discontinuity
💡Coordinate pair
💡Increasing function
💡First derivative
Highlights
Local and global extrema refer to the minimums and maximums of a function.
A local maximum or minimum is determined by comparing a point to its surrounding neighborhood.
The red curve example demonstrates a function that is strictly increasing with no local extrema.
Critical points are essential for identifying local extrema as they occur where the first derivative is zero.
The slope of the tangent line at a point helps determine if it's a local maximum or minimum.
A local minimum occurs at a critical point where the second derivative is positive.
A local maximum occurs at a critical point where the second derivative is negative.
Extrema is an umbrella term for all extreme values, including local minima and maxima.
A global minimum is the lowest possible value of the function, which might occur at multiple points.
A global maximum is the highest possible value of the function, also possibly at multiple points.
When asked for a minimum or maximum, it's good practice to provide the coordinate pair (x and y values).
For non-differentiable points, such as sharp turns in a function, local extrema can occur without being critical points.
Piecewise functions may have local extrema that do not occur at critical points and may not be continuous.
It's important to consider the domain and differentiability when identifying local extrema in piecewise functions.
The video provides examples to illustrate the concepts of local and global extrema in various function scenarios.
Understanding the behavior of a function's derivative is crucial for identifying extrema.
The video clarifies the conditions under which a point is considered a local or global extremum.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: