Solve related rates rising hot air balloon

Brian McLogan
30 Nov 201710:35
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses a mathematical problem involving a rising balloon observed from a distance of 500 feet. The problem introduces the angle of elevation at 45 degrees, which increases at 0.14 radians per minute. The goal is to determine the rate at which the balloon is rising. By using the tangent function and its derivative, the relationship between the angle, the height of the balloon, and the horizontal distance is established. The solution involves applying the quotient rule and chain rule to find the rate of change of the balloon's height with respect to time, resulting in the balloon rising at 140 feet per minute.

Takeaways
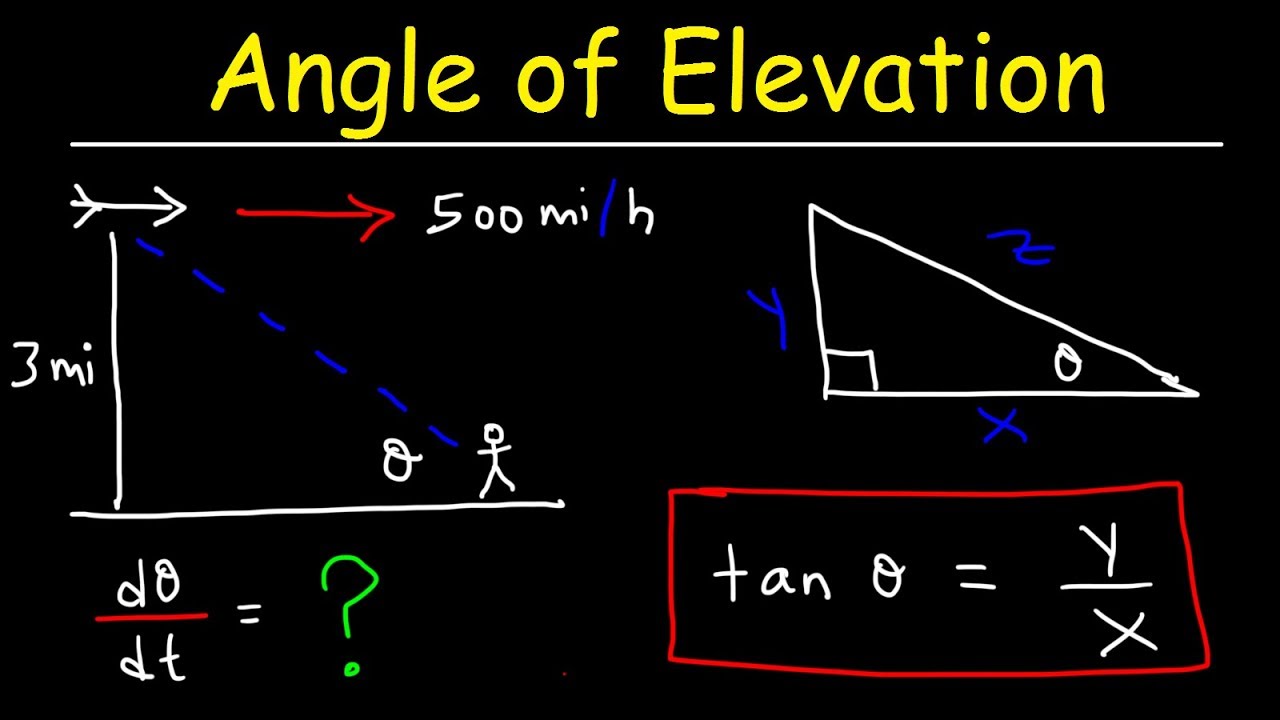
  • ๐ŸŽˆ The example discusses a balloon rising from the ground at an initial distance of 500 feet from liftoff.
  • ๐Ÿ“ The angle of elevation at liftoff is 45 degrees, which is equivalent to ฯ€/4 radians.
  • ๐Ÿ“ˆ The angle of elevation increases at a rate of 0.14 radians per minute.
  • ๐Ÿ”„ The problem involves converting the problem from degrees to radians for consistency.
  • ๐Ÿ“Š A right triangle is formed with the ground, and the Pythagorean theorem is initially considered but not used.
  • ๐Ÿ”ข A relationship between the angle (ฮธ), the opposite side (y), and the adjacent side (x) is needed, leading to the use of the tangent function.
  • ๐Ÿ‘“ The tangent relationship is expressed as tan(ฮธ) = y/x, with x being the constant 500 feet.
  • ๐Ÿš€ The derivative of the tangent function is used to find the rate of change of y with respect to time (dy/dt).
  • ๐Ÿงฎ The derivative calculation involves the use of the chain rule and the understanding of the relationship between the angle's rate of change (dฮธ/dt) and the distance (y).
  • ๐Ÿ“ˆ The final calculation results in the rate at which the balloon is rising, which is 140 feet per minute with a calculator or 500 * 2 * 0.14 without one.
  • ๐Ÿค” The script emphasizes the importance of understanding the relationships in the problem and the application of calculus concepts to solve real-world scenarios.
Q & A

  • What is the initial height of the balloon from the ground?

    -The initial height of the balloon from the ground is 500 feet.

  • What is the angle of elevation at liftoff?

    -The angle of elevation at liftoff is 45 degrees, which is equivalent to ฯ€/4 radians.

  • How is the angle of elevation changing over time?

    -The angle of elevation is increasing at a rate of 0.14 radians per minute.

  • What relationship between the angle, opposite side, and adjacent side of a right triangle is used in the problem?

    -The tangent relationship, where tan(ฮธ) = y/x, is used in the problem.

  • Why is it beneficial to plug in known values before taking the derivative?

    -Plugging in known values before taking the derivative simplifies the process and often avoids the need for more complex rules like the quotient rule, making the problem easier to solve.

  • What derivative are we interested in calculating with respect to time?

    -We are interested in calculating the rate of change of y with respect to time (dy/dt), which represents how fast the balloon is rising.

  • What is the final result of the rate at which the balloon is rising?

    -The final result of the rate at which the balloon is rising is 140 feet per minute, assuming the use of a calculator for precise computation.

  • How can the secant function be simplified for ฯ€/4 radians?

    -The secant function for ฯ€/4 radians can be simplified by referring to the unit circle, where sec(ฯ€/4) is equivalent to the square root of 2, thus sec^2(ฯ€/4) equals 2.

  • What is the significance of the given rate of change of the angle (dฮธ/dt) in solving the problem?

    -The given rate of change of the angle (dฮธ/dt) is crucial for determining the rate at which the balloon is rising, as it is used in the derivative calculation to find dy/dt.

  • How does the problem illustrate the application of trigonometric functions in real-world scenarios?

    -The problem demonstrates the application of trigonometric functions by using the angle of elevation and its rate of change to determine the rising speed of a balloon, showing how these mathematical concepts can be applied to model and analyze real-world phenomena.

Outlines
00:00
๐ŸŽˆ Balloon Ascension and Angle of Elevation

The paragraph discusses a scenario where a balloon is rising from the ground at an angle of elevation of 45 degrees. The speaker explains the given conditions, such as the balloon being 500 feet from liftoff and the angle of elevation increasing at a rate of 0.14 radians per minute. The speaker transitions from degrees to radians for problem-solving and introduces the concept of the rate of change, emphasizing the need to find the balloon's rising speed. The Pythagorean theorem is mentioned but deemed unnecessary for this problem, and the focus shifts to creating a relationship between the angle, the height of the balloon, and the horizontal distance (x). The tangent function is introduced as the key relationship, and the speaker begins to set up the equation for solving the problem.

05:04
๐Ÿ“š Derivative Calculation and Secant Rule

This paragraph delves into the mathematical process of differentiating with respect to time (t) to find the rate at which the balloon is rising. The speaker differentiates the tangent function, applying the chain rule, and discusses the importance of plugging in known values before taking derivatives. The concept of secant squared is introduced, and the speaker provides a detailed explanation of how to calculate the derivative, including the use of the unit circle to find the secant value for 45 degrees. The speaker then sets up the equation to solve for the rate of change of the balloon's height (dy/dt).

10:04
๐Ÿš€ Solving for the Balloon's Ascension Rate

The speaker concludes the problem by solving for the balloon's ascension rate. They calculate the secant squared value for 45 degrees, apply the given rate of change of the angle (0.14 radians per minute), and use the relationship between the angle, the height, and the distance to find the derivative (dy/dt). The speaker then multiplies by 500 to isolate dy/dt and provides the final answer of 140 feet per minute with the use of a calculator. The speaker also offers an alternative solution for those without a calculator, emphasizing the importance of understanding the process and the ability to leave the answer in a simplified form if necessary.

Mindmap
Keywords
๐Ÿ’กballoon
In the context of the video, a 'balloon' refers to an object that is rising from the ground. The balloon's ascent is the central focus of the problem being discussed, with the goal of determining the rate at which it is rising at a specific moment. The balloon's height and the angle of elevation are key elements used in the mathematical calculations.
๐Ÿ’กangle of elevation
The 'angle of elevation' is the angle above the horizontal plane that a viewer's line of sight makes with the horizontal when observing an object, in this case, the balloon. It is a critical concept in the video, as the angle is given as 45 degrees and is used to establish the initial conditions for the mathematical problem.
๐Ÿ’กradians
Radians are a unit of measure used to express angles in the field of mathematics. Unlike degrees, which are often used in everyday language, radians are more commonly used in advanced mathematics and physics. In the video, the rate of change of the angle of elevation is given in radians per minute, emphasizing the use of radians for precise calculations.
๐Ÿ’กpythagorean theorem
The Pythagorean theorem is a fundamental principle in geometry that states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In the video, the theorem is mentioned as a potential tool to solve the problem but is not directly used, as the problem is re-framed in terms of the tangent function.
๐Ÿ’กtangent
The 'tangent' of an angle in a right triangle is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. In the video, the tangent function is used to establish a relationship between the height (y) and the horizontal distance (x) of the balloon from the observer, which is essential for calculating the rate at which the balloon is rising.
๐Ÿ’กderivative
In calculus, a 'derivative' represents the rate of change of a function with respect to a variable. It is used to analyze the behavior of functions, particularly in terms of their rates of change and slopes of tangents. In the video, the derivative is sought to find out how fast the balloon is rising at a specific moment, which is the central problem being solved.
๐Ÿ’กchain rule
The 'chain rule' is a fundamental technique in calculus used to compute the derivative of a composite function. It states that the derivative of a function composed of multiple functions is the derivative of the outer function times the derivative of the inner function. In the video, the chain rule is implied when discussing the calculation of the derivative of the tangent function with respect to time.
๐Ÿ’กsecant
The 'secant' function in trigonometry is the reciprocal of the cosine function. It represents the ratio of the hypotenuse to the adjacent side in a right triangle. In the video, the secant function is used in the calculation of the rate at which the balloon is rising, as it is related to the derivative of the tangent function.
๐Ÿ’กrate of change
The 'rate of change' refers to the speed at which a quantity changes with respect to another variable. It is a central concept in calculus and is used to analyze various dynamic systems. In the video, the rate of change is the main focus, as the problem aims to determine how fast the balloon is rising at a specific moment in time.
๐Ÿ’กquotient rule
The 'quotient rule' is a calculus technique used to find the derivative of a quotient of two functions. It states that the derivative of a function divided by another function is the derivative of the numerator times the denominator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. In the video, the quotient rule is mentioned as a potential method but is not used, as the problem is simplified to avoid its application.
๐Ÿ’กunit circle
The 'unit circle' is a circle with a radius of 1 unit in the coordinate plane, where the center is at the origin. It is a fundamental tool in trigonometry for defining trigonometric functions and understanding their relationships. In the video, the unit circle is referred to when discussing the secant of pi/4 or 45 degrees, which is needed to calculate the rate of the balloon's ascent.
Highlights

The problem involves a balloon rising from the ground at an angle of elevation of 45 degrees.

The balloon is 500 feet from liftoff, providing a specific distance for calculations.

The angle of elevation increases at a rate of 0.14 radians per minute.

The initial angle of elevation is equivalent to 45 degrees or ฯ€/4 radians.

The problem is conceptualized to avoid using the quotient rule, aiming for a more straightforward solution.

The relationship between the angle, opposite side, and adjacent side of a right triangle is given by the tangent function.

The derivative of the tangent function with respect to time is used to find the rate of change of the balloon's height.

The Pythagorean theorem is not directly applicable as it does not involve the angle ฮธ.

The secant function is introduced as the derivative of the tangent squared to find the rate of change of the balloon's height.

The chain rule is applied to find the derivative of the secant squared in relation to time.

The value of secant at 45 degrees (ฯ€/4 radians) is calculated using the unit circle.

The final calculation involves multiplying the secant squared value by the given rate of change of the angle and the distance from liftoff.

The balloon's rising rate is determined to be 140 feet per minute with the use of a calculator.

A non-calculator approach is also discussed, where the exact numerical result is not required.

The problem emphasizes the importance of understanding the relationship between trigonometric functions and their derivatives.

The solution process highlights the application of calculus in real-world scenarios, such as tracking the motion of a rising balloon.

Transcripts

Browse More Related Video

How solve a problem with changing angle for related rates

Related Rates - Angle of Elevation Problem

3.9 #42 Related Rates Ferris Wheel Angular Velocity and Right Triangle Trig

Learn how to find the change in theta for a triangle, related rates

Related Rates - Filling a Cone Problem

Related rates: water pouring into a cone | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsMathematicsTrigonometryDerivativesTangentAngle of ElevationRising SpeedEducational ContentProblem SolvingConceptual Explanation