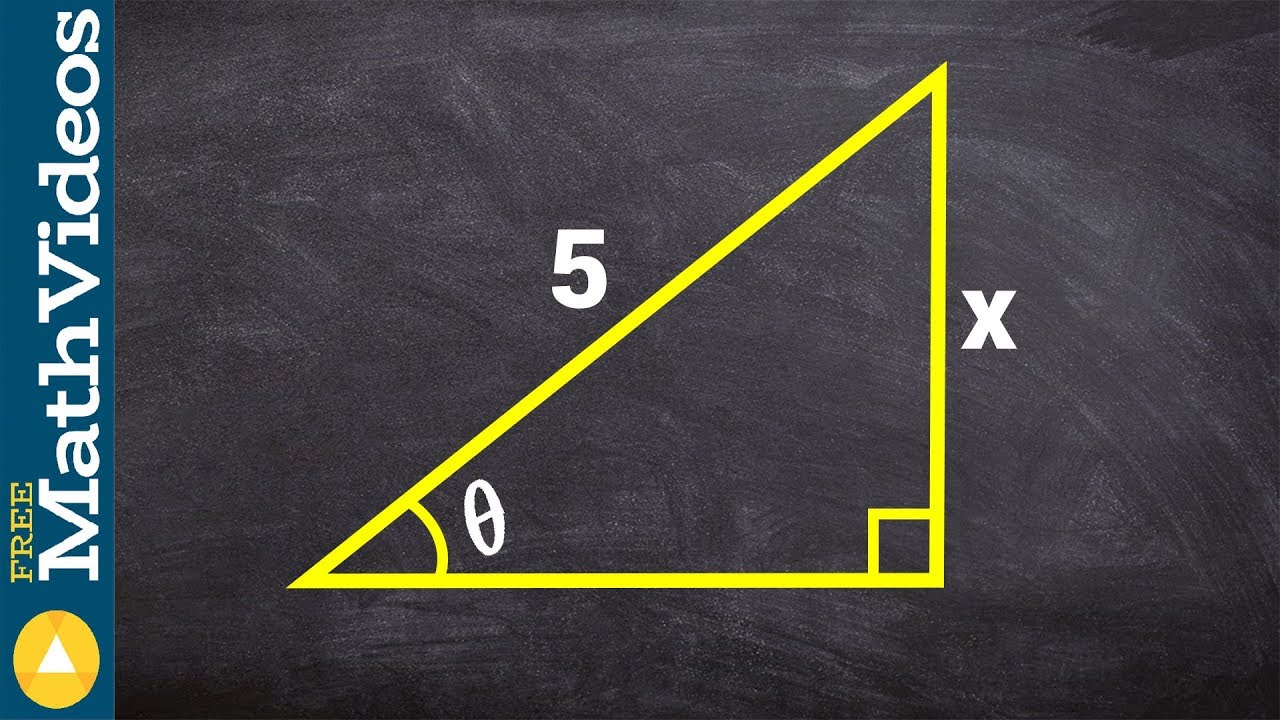3.9 #42 Related Rates Ferris Wheel Angular Velocity and Right Triangle Trig
TLDRThe video script discusses a physics problem involving a Ferris wheel with a radius of 10 meters, making one revolution every two minutes. It explains how to calculate the rate at which a person is rising when they are 16 meters above the ground. The solution involves identifying the rotational velocity, setting up a right triangle with the person's height (h), and using trigonometric relationships to find the derivative of y with respect to time (dy/dt). The script guides through converting angular velocity to radians per minute, isolating y as 10 times the sine of theta, and then differentiating to find the person's rising speed. The final answer is given as 8π meters per minute, showcasing a clear application of calculus in physics.
Takeaways
- 🎡 The problem involves calculating the speed at which a person on a Ferris wheel is rising when they are 16 feet (or meters) above the ground.
- 🔢 The radius of the Ferris wheel is given as 10 meters, and it completes one revolution every two minutes.
- 📐 The problem is approached by considering the Ferris wheel's rotational motion and the geometry of the situation, specifically using a right triangle with the person's height as one side.
- ⏱ The angular velocity of the Ferris wheel is determined to be π radians per minute, which is derived from its one revolution every two minutes.
- 📚 The rate of change of the angle (dθ/dt) is identified as a key factor in solving the problem, as it represents the rotational speed of the wheel.
- 🤔 The person's rising speed is related to the change in height (dh/dt), but the focus shifts to the change in the vertical component of the person's position (dy/dt) since it's easier to relate to the angle θ.
- 👉 The relationship between the person's vertical position (y) and the angle (θ) is established using the sine function, with y = 10 * sin(θ).
- 🧐 The derivative of y with respect to time (dy/dt) is calculated using the chain rule, resulting in 10 * cos(θ) * (dθ/dt).
- 📐 To find the specific value of dy/dt when y is 6 meters, the cosine of θ is determined using the Pythagorean theorem, recognizing the 3-4-5 triangle ratio in the context of the Ferris wheel's geometry.
- 📈 The final calculation of dy/dt when y is 6 meters results in 8π meters per minute, indicating the speed at which the person is rising at that point.
- 📝 The solution process emphasizes the importance of understanding both the rotational motion and the geometric relationships involved in the problem.
Q & A
What is the problem being discussed in the script?
-The problem involves calculating the speed at which a person is rising on a Ferris wheel when they are 16 feet (or meters) above the ground, given that the wheel has a radius of 10 meters and completes one revolution every two minutes.
What is the first step suggested to solve the Ferris wheel problem?
-The first step is to identify the rotational velocity of the Ferris wheel, which is given as one revolution every two minutes.
How is the angular velocity of the Ferris wheel expressed in the script?
-The angular velocity is initially expressed as one revolution per two minutes, which is then converted to radians per minute, resulting in π radians per minute.
What is the significance of the angle θ in the problem?
-The angle θ is the angle at the central axis of the Ferris wheel where it is rotating, and it represents the rate of change of the wheel's position, which is crucial for finding the speed of the person's rise.
Why is a right triangle used in the problem?
-A right triangle is used to relate the height of the person (y) to the radius of the Ferris wheel (10 meters) and to express the relationship using trigonometric functions.
What is the relationship between y (vertical section) and h (height of the person)?
-The relationship is that the difference between y and h is constant, with a 10-meter gap representing the radius of the Ferris wheel.
How is the height y related to the angle θ in the script?
-The height y is related to the angle θ through the equation y = 10 * sin(θ), using the sine function to represent the opposite side of the right triangle over the hypotenuse.
What is the derivative dθ/dt, and why is it important for the problem?
-The derivative dθ/dt is the rate of change of the angle θ with respect to time t, which is equal to π radians per minute. It is important because it represents the angular velocity of the Ferris wheel and is used to find the rate of change of y with respect to time.
How is the rate of change of y with respect to time (dy/dt) calculated?
-The rate of change of y with respect to time (dy/dt) is calculated by taking the derivative of y with respect to time, which results in 10 * cos(θ) * dθ/dt.
At the moment when the person's height h is 16, what is the value of y?
-When the person's height h is 16, the value of y (the vertical section of the right triangle) is 6 meters.
How is the cosine of θ determined when y is 6?
-The cosine of θ is determined using the Pythagorean theorem or recognizing the 3-4-5 triangle ratio, where the adjacent side to the angle θ is 8 meters, making cos(θ) equal to 8/10 or 4/5.
What is the final calculation for the rate at which the person is rising when y is 6?
-The final calculation for the rate at which the person is rising when y is 6 is 10 * (8/10) * π, which simplifies to 8π meters per minute.
Outlines
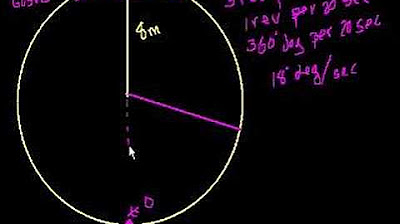
🎡 Understanding the Ferris Wheel Problem
The script discusses a physics problem involving a Ferris wheel that completes one revolution every two minutes. The problem is to determine the rate at which a person is rising when they are 16 feet above the ground, given the radius of the wheel is 10 meters. The script begins by establishing the rotational velocity of the Ferris wheel, which is converted into angular velocity in radians per minute. The angular velocity \( \frac{d\theta}{dt} \) is calculated to be \( \pi \) radians per minute. The script then sets up a right triangle to relate the vertical position \( y \) of the person to the angle \( \theta \) at the center of the wheel, aiming to find \( \frac{dy}{dt} \) when \( h \) (the height above the ground) is 16 meters.
📐 Calculating the Rate of Ascent on a Ferris Wheel
Continuing from the setup in the previous paragraph, the script derives an equation relating \( y \) and \( \theta \) using the sine function, resulting in \( y = 10 \sin(\theta) \). The derivative of \( y \) with respect to time \( t \), \( \frac{dy}{dt} \), is then calculated to be \( 10 \cos(\theta) \frac{d\theta}{dt} \). Knowing \( \frac{d\theta}{dt} \) as \( \pi \) radians per minute, the script focuses on finding \( \cos(\theta) \) when \( y \) is 6 meters (which corresponds to \( h \) being 16 meters). Using the properties of a right triangle and the Pythagorean theorem, \( \cos(\theta) \) is determined to be \( \frac{8}{10} \) or 0.8. Substituting the known values, \( \frac{dy}{dt} \) at that moment is calculated to be \( 8\pi \) meters per minute, indicating the person's rate of ascent.
Mindmap
Keywords
💡Ferris Wheel
💡Revolution
💡Rotational Velocity
💡Radians
💡Angular Velocity
💡Right Triangle
💡Trigonometric Functions
💡Derivative
💡Pythagorean Theorem
💡Rate of Change
Highlights
Understanding the problem setup of a person on a ferris wheel with one revolution every two minutes and a 10-meter radius.
Introduction to rotational velocity and its significance in solving the problem.
Explanation of the relationship between the ferris wheel's angular velocity and the change in the person's height.
Establishing the use of radians for angular measurements instead of degrees.
Calculation of the angular velocity as pi radians per minute.
Clarification on the relationship between height (h) and vertical position (y) in the context of the ferris wheel.
Simplification of the problem by focusing on the change in y (dy/dt) instead of h (dh/dt).
Establishing the relationship between y and theta using trigonometric functions.
Derivation of the equation y = 10 sin(theta) for the vertical position y.
Taking the derivative with respect to time to find dy/dt.
Utilization of the known angular velocity (d(theta)/dt) to substitute into the derivative equation.
Simplification of the problem by recognizing the cosine of theta can be determined without directly finding theta.
Use of the Pythagorean theorem to find the adjacent side of the triangle formed by y and the hypotenuse.
Final calculation of the rate at which the person is rising as 8pi meters per minute.
Summary of the solution and validation of the final result.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: