Learn how to find the change in theta for a triangle, related rates
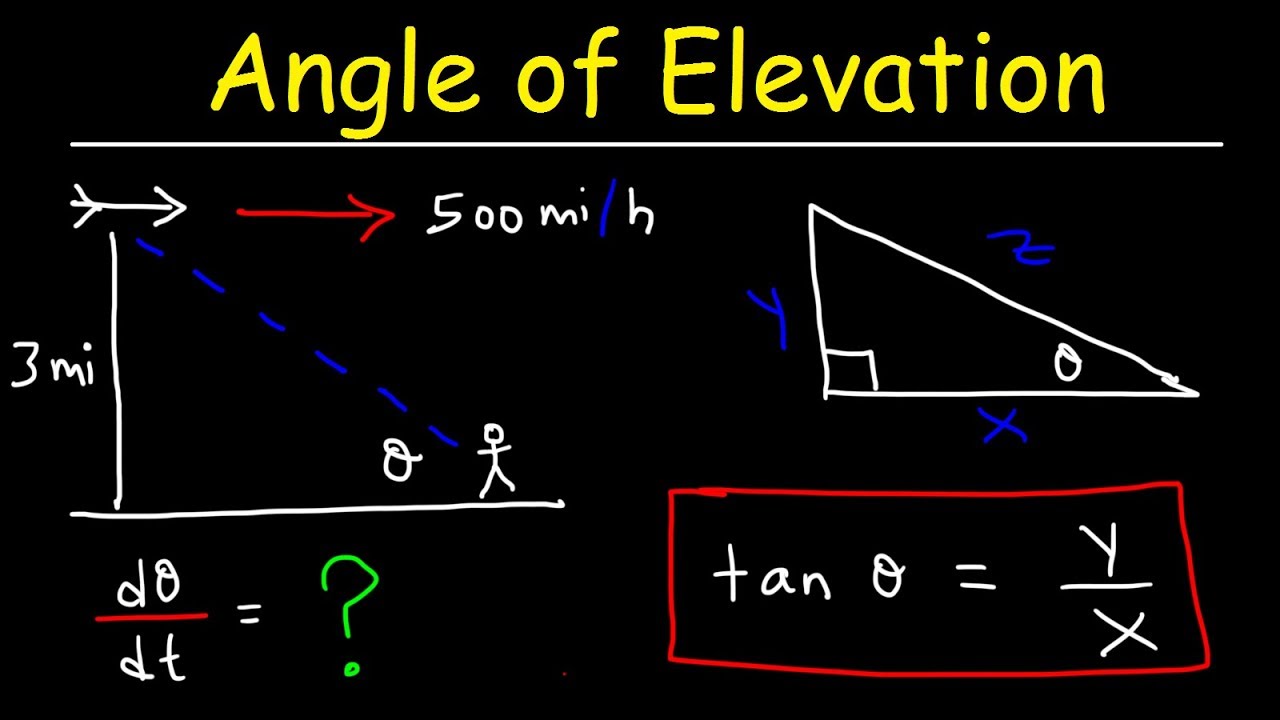
TLDRThe transcript discusses a math problem involving a right triangle with a hypotenuse of 5 units and an opposite side of 3 units. It explains that as the angle theta increases at a constant rate of three radians per minute, the goal is to find the rate at which the side length x is increasing when x equals 3 units. By utilizing the Pythagorean triple (3,4,5) and trigonometric functions, specifically sine and cosine, the problem is solved by differentiating the equation with respect to time. The final result, when calculated correctly, gives the rate of change of x (dx/dt) as 12 units per minute.
Takeaways
- 📌 The problem involves a triangle with a rate of change of theta (d theta/dt) at three radians per minute.
- 📐 The triangle is a right triangle with sides represented by theta, 5, and x.
- 🔢 The relationship between the sides and angle is given by the trigonometric function sine, i.e., sin(theta) = opposite/hypotenuse.
- 🏹 The triangle is identified as a 3-4-5 Pythagorean triple, which is a common right triangle in mathematics.
- 🌟 The derivative of sine with respect to time (t) is used to find the rate of change of x (dx/dt).
- 🔄 The chain rule is applied when differentiating the equation with respect to time, involving the derivative of theta with respect to time (d theta/dt).
- 📈 The cosine of theta is found to be 4/5, using the adjacent/hypotenuse ratio from the 3-4-5 triangle.
- 📚 The given rate of change of theta (d theta/dt = 3 radians/min) is used to find the rate of change of x (dx/dt).
- 🔢 By solving for dx/dt, it is found to be 12 units per minute when x equals 3 units.
- 📋 The process emphasizes the importance of not simplifying too early, especially without a calculator, to avoid losing track of intermediate steps.
- 👉 The solution involves multiplying the given rate of change of theta by the ratio of the adjacent side to the hypotenuse, adjusted for the Pythagorean triple.
Q & A
What is the rate of change of theta (d theta/dt) mentioned in the transcript?
-The rate of change of theta (d theta/dt) is three radians per minute.
What type of triangle is mentioned in the script?
-A right triangle is mentioned in the script.
What is the relationship between the sides of the triangle and theta?
-The relationship between the sides of the triangle and theta is represented by the trigonometric ratio sine, where sine of theta is equal to the opposite side over the hypotenuse.
What is the significance of the 3-4-5 triangle in the context of this script?
-The 3-4-5 triangle is a Pythagorean triple, which is a set of three positive integers that satisfy the Pythagorean theorem. In this context, it helps in identifying the triangle as a right triangle and assists in calculating the rate of change of x (dx/dt).
How is the rate of change of x with respect to time (dx/dt) represented in the script?
-The rate of change of x with respect to time (dx/dt) is represented as being equal to one-fifth of the rate of change of theta with respect to time (d theta/dt).
What trigonometric function is used to find the rate of change of x (dx/dt)?
-The cosine function is used to find the rate of change of x (dx/dt), as cosine of theta is equal to the adjacent side over the hypotenuse.
What is the value of cosine of theta in the context of the 3-4-5 triangle?
-In the context of the 3-4-5 triangle, the value of cosine of theta is four over five.
How is the chain rule applied in this scenario?
-The chain rule is applied by taking the derivative of sine of theta with respect to time, which results in cosine of theta multiplied by the rate of change of theta with respect to time (d theta/dt).
What is the final calculated value of dx/dt when x equals 3 units?
-The final calculated value of dx/dt when x equals 3 units is 12 units per minute.
Why is it important not to simplify the equation too early when solving problems like this?
-It is important not to simplify the equation too early because it can help avoid errors and make the calculation process easier to follow, especially when a calculator is not available.
How does the process of differentiating with respect to a different variable affect the outcome?
-Differentiating with respect to a different variable requires the use of the chain rule, which involves taking the derivative of the function with respect to the variable of interest and then multiplying it by the derivative of the variable itself.
Outlines
📚 Mathematical Analysis of a Triangle's Rate of Change
This paragraph delves into the mathematical analysis of a triangle where one side is increasing at a constant rate. The focus is on understanding the relationship between the rate of change of angle theta (d theta/dt) and the rate of change of side length x (dx/dt). The speaker introduces a right triangle with known dimensions and explains the need to use trigonometric ratios to find the unknown rate of change. The paragraph highlights the use of sine and cosine functions, the Pythagorean triple (3,4,5), and the application of differentiation rules, specifically the chain rule, to solve for dx/dt when x equals 3 units. The process involves differentiating the sine function with respect to time and using the cosine function to find the derivative of dx/dt. The explanation emphasizes the importance of not prematurely simplifying equations and the methodical approach to solving the problem.
📈 Solving for dx/dt using the Pythagorean Triple
In this paragraph, the speaker continues the mathematical discussion by focusing on solving for the rate of change of x (dx/dt) using the previously established trigonometric relationship. The speaker utilizes the known Pythagorean triple (3,4,5) to determine the cosine of theta, which is the ratio of the adjacent side to the hypotenuse. With the given rate of change of theta (d theta/dt) as three radians per minute, the speaker sets up an equation to solve for dx/dt. By applying the chain rule and multiplying the known values, the speaker arrives at the final answer, which is 12 units per minute (answer E). This conclusion wraps up the mathematical problem-solving process, demonstrating the application of trigonometry and calculus in a practical scenario.
Mindmap
Keywords
💡triangle
💡theta
💡radians
💡right triangle
💡differentiation
💡sine
💡cosine
💡Pythagorean triple
💡chain rule
💡rates of change
💡implicit differentiation
Highlights
The problem involves a triangle with a constant rate of change of theta.
Theta increases at a rate of three radians per minute, represented as d theta dt equals three radians per minute.
The triangle is a right triangle with sides theta, 5, and x.
The goal is to find the rate at which x is increasing, represented as dx dt.
The specific condition given is to find dx dt when x equals 3 units.
The triangle's dimensions suggest it is a 3-4-5 Pythagorean triple.
The use of trigonometric ratios is essential in solving the problem, specifically sine and cosine.
The derivative of sine with respect to theta is used, which is cosine of theta.
Chain rule is applied to differentiate the equation with respect to time t.
Cosine of theta is determined to be four over five, based on the Pythagorean triple.
The relationship between d theta dt and dx dt is established as one fifth of dx dt.
To solve for dx dt, the equation is multiplied by five, leading to a simplified calculation.
The final answer for dx dt when x equals 3 units is 12 units per minute.
The problem-solving approach emphasizes the importance of not simplifying too early, especially without a calculator.
The method showcases the application of implicit differentiation in rates problems.
The use of the 3-4-5 triangle is highlighted as a key to quickly identifying the relationship between the sides.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: