Related rates: water pouring into a cone | AP Calculus AB | Khan Academy
TLDRThe video script presents a mathematical problem involving a conical cup being filled with water at a rate of 1 cubic centimeter per second. The cup has a height of 4 centimeters with a top diameter of the same length. The challenge is to determine the rate at which the height of the water in the cup is changing when the water level is at 2 centimeters. By applying the formula for the volume of a cone and using calculus, specifically the chain rule, the video explains how to find the derivative of the volume with respect to time to solve for the rate of change of the water level's height, resulting in an answer of 1 over pi centimeters per second when the water height is 2 centimeters.
Takeaways
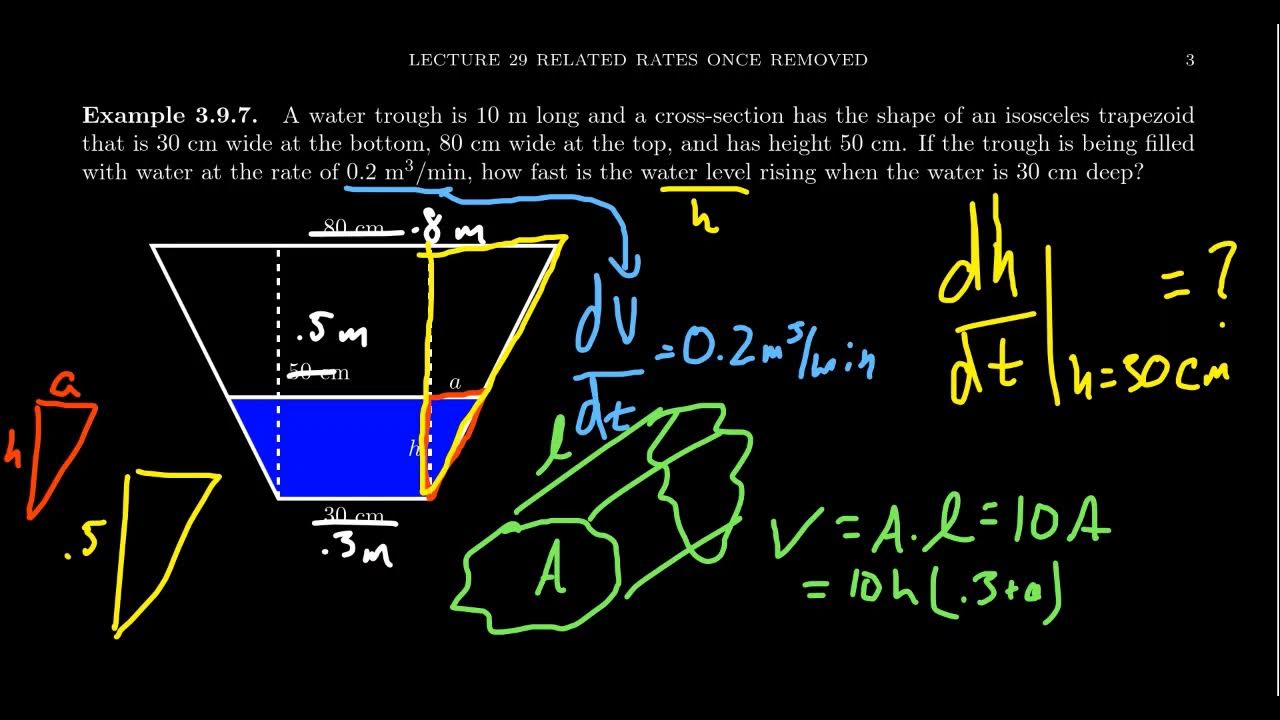
- 📌 The scenario involves a conical thimble-like cup with a height and top diameter of 4 centimeters.
- 💧 The cup is being filled with water at a rate of 1 cubic centimeter per second.
- 📈 At a specific moment, there are 2 centimeters of water in the cup.
- 🔍 The goal is to find the rate at which the height of the water is changing with respect to time.
- 📊 The relationship between the volume and height of the cone is given by the formula for the volume of a cone, which is 1/3 times the base area times the height.
- 🌀 The volume of water in the cup at any time is given by the formula πh²/4, where h is the height of the water.
- 🅿️ To find the rate of change of height, a derivative is taken with respect to time, applying the chain rule for the power function.
- 📝 The derivative of the volume with respect to time (dV/dt) is equal to (π/12) * 3 * h² * (dh/dt).
- 🎯 At the moment when the water height is 2 centimeters, the known rate of volume change (dV/dt) is 1 cubic centimeter per second.
- 🧮 By solving the equation for (dh/dt), we find that the rate of change of the water height with respect to time is 1/π centimeters per second.
- 🚦 The answer is dimensionally consistent, indicating the rate of height change in centimeters per second.
Q & A
What is the shape of the cup described in the transcript?
-The cup is described as conical or thimble-like.
What are the dimensions of the cup?
-The cup is 4 centimeters high, and the diameter of the top of the cup is also 4 centimeters.
What is the rate at which water is being poured into the cup?
-Water is being poured into the cup at a rate of 1 cubic centimeter per second.
How much water is currently in the cup?
-There is currently 2 centimeters of water in the cup.
What is the relationship between the volume of the water in the cup and its height?
-The volume of water in the cup is given by the formula for the volume of a cone, which is 1/3 times the area of the base (which is pi times the radius squared) times the height (h). So, the volume is (1/3) * π * (h/2)^2 * h.
How is the rate of change of the water height with respect to time derived?
-The rate of change of the water height with respect to time is derived by taking the derivative of the volume with respect to time, using the chain rule to account for the volume as a function of height.
What is the derivative of the volume of the water with respect to time?
-The derivative of the volume of the water with respect to time, dV/dt, is equal to (π/12) * 3 * h^2 * dh/dt.
What is the initial condition given for the height of the water?
-The initial condition given for the height of the water is that it is 2 centimeters at the moment of interest.
What is the final answer for the rate at which the height of the water is changing with respect to time?
-The final answer for the rate at which the height of the water is changing with respect to time is 1/π centimeters per second, when the height is 2 centimeters.
How does the ratio of the diameter to the height of the cup affect the calculation?
-The ratio of the diameter to the height of the cup remains constant (1:1) regardless of the water level, which allows us to determine that the diameter of the water surface at any height h is also h, and thus derive the area of the water surface in terms of h.
What mathematical concept is used to relate a changing volume to a changing height?
-The mathematical concept used to relate a changing volume to a changing height is the derivative, specifically the chain rule for differentiation.
Outlines
💡 Introduction to the Cone Filling Problem
The paragraph introduces a mathematical problem involving a conical cup being filled with water. The cup's dimensions are given, with a height and top diameter of 4 centimeters. Water is being poured into the cup at a rate of 1 cubic centimeter per second, and at the moment of discussion, the water level is 2 centimeters high. The main question posed is to determine the rate at which the height of the water in the cup is changing at this specific moment.
📚 Deriving the Relationship Between Volume and Height
The paragraph focuses on establishing a mathematical relationship between the volume of water in the cone and its height. It uses the formula for the volume of a cone, which is 1/3 times the base area times the height. By considering the dimensions of the cup and the water level, an expression for the volume in terms of the height of the water is derived. The paragraph then discusses the next step, which involves taking the derivative of this volume-height relationship with respect to time to find the rate of change of the water height.
🧮 Calculating the Rate of Change of Water Height
In this paragraph, the derivative of the volume-height relationship is calculated to find the rate at which the height of the water is changing. The chain rule is applied to differentiate the volume function with respect to time. The known rate of water pouring (1 cubic centimeter per second) and the current height of the water (2 centimeters) are used to set up an equation. By solving this equation, the rate of change of the water height with respect to time is determined to be 1 over pi (approximately 0.3183) centimeters per second when the water height is 2 centimeters.
Mindmap
Keywords
💡Conical Thimble-like Cup
💡Volume
💡Height
💡Derivative
💡Rate
💡Chain Rule
💡Pi (π)
💡Base Area
💡Water Pouring
💡Constant Rate
💡Function of Time
Highlights
The scenario involves a conical thimble-like cup with a height and diameter of 4 centimeters.
Water is being poured into the cup at a rate of 1 cubic centimeter per second.
At the moment of discussion, there is 2 centimeters of water height in the cup.
The problem is to find the rate at which the height of the water is changing with respect to time.
The relationship between the volume and height of the cone at any given moment is derived from the volume formula of a cone.
The volume of the water in the cup is given by the formula pi * (h^3) / 12, where h is the height of the water.
To find the rate of change of height with respect to time, the derivative of the volume with respect to time is taken.
The derivative of the volume with respect to time is equal to the constant rate of water pouring (1 cm³/s) times the derivative of height with respect to time.
The chain rule is applied to find the derivative of the height function with respect to time.
The rate of change of height with respect to time is found to be 1/π centimeters per second when the height is 2 centimeters.
The problem demonstrates the application of calculus concepts, such as derivatives and the chain rule, to real-world scenarios.
The solution involves understanding the geometry of a cone and its relationship with volume and height.
The problem-solving process highlights the importance of establishing relationships and taking derivatives to solve for rates of change.
The use of the volume formula for a cone is a key step in setting up the problem for solution.
The problem serves as an example of how physical quantities can be related through mathematical modeling.
The solution requires the integration of algebraic manipulation and calculus to arrive at the final rate of change.
The final answer, 1/π cm/s, demonstrates the precision that can be achieved through mathematical analysis.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: