How solve a problem with changing angle for related rates
TLDRThe transcript describes a mathematical problem involving an airplane flying at an altitude of five miles and a speed of 600 miles per hour. The objective is to calculate the rate at which the angle of elevation, theta, changes when theta is 30 degrees. The solution process involves understanding the relationship between height, horizontal distance, and angle of elevation, and applying derivatives to find the rate of change. The final answer is obtained by incorporating the given values into the derived formula, resulting in a rate of change of 30 radians per hour, or 600 degrees per hour.
Takeaways
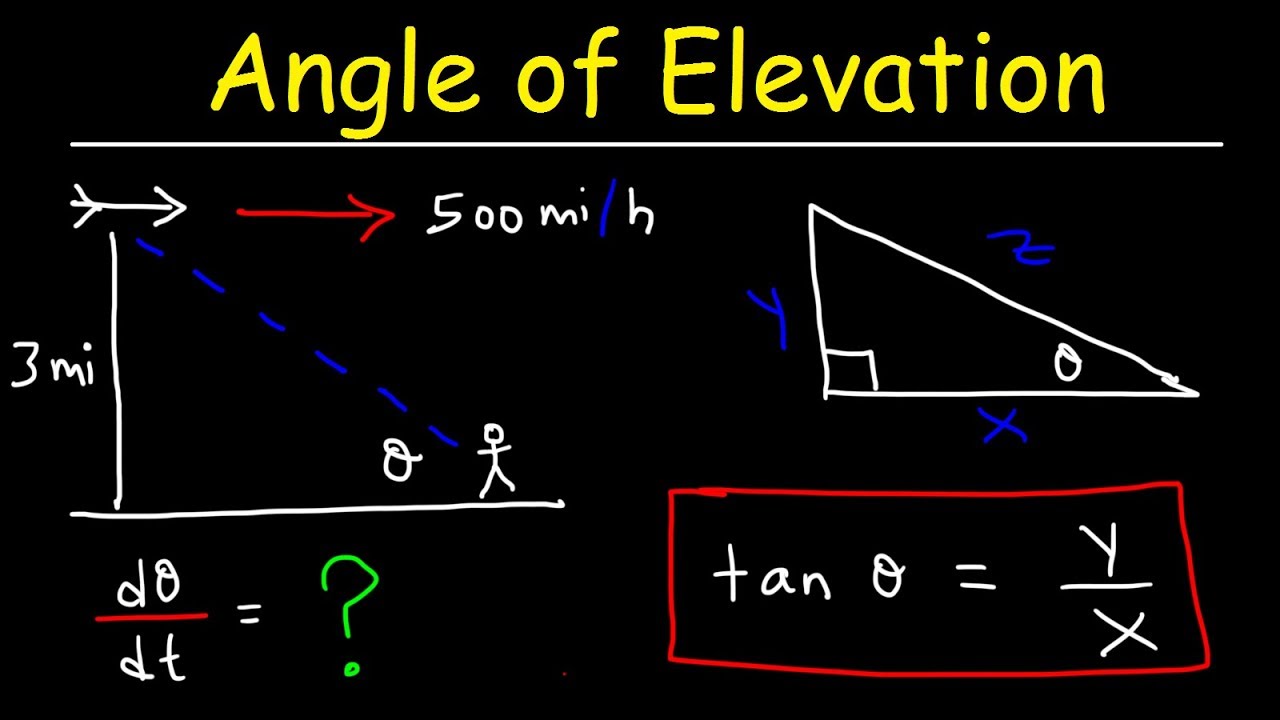
- 🛫 The problem involves an airplane flying at an altitude of 5 miles towards a point directly over an observer.
- 🚦 The speed of the airplane is given as 600 miles per hour.
- 📐 The task is to find the rate at which the angle of elevation (θ) is changing when θ equals 30 degrees.
- 🤔 The height (h) of the airplane is constant at 5 miles and does not change as the airplane moves.
- 🌐 The horizontal distance (x) from the observer to the point directly under the airplane is unknown but can be calculated.
- 🔄 The rate of change of distance (dx/dt) is equal to the airplane's speed, which is 600 miles per hour.
- 📐 The relationship between height, horizontal distance, and angle of elevation is given by the equation: tan(θ) = h/x.
- 🔢 At θ = 30 degrees, x can be found using the tangent function: x = h/tan(30°) = 5 miles / tan(30°) ≈ 8.66 miles.
- 🎓 The derivative of tan(θ) with respect to time (t) is used to find the rate of change of the angle of elevation: d(tan(θ))/dt = sec^2(θ) * (dθ/dt).
- 📌 The final formula to find dθ/dt when θ = 30 degrees is: dθ/dt = -5 * cos^2(θ) / x^2.
- 📈 By substituting the known values (x ≈ 8.66 miles and cos(30°) = √3/2), the rate of change of the angle of elevation is approximately 30 radians per hour or 600 degrees per hour.
Q & A
What is the scenario being discussed in the script?
-The script discusses a mathematical problem involving an airplane flying at an altitude of five miles towards a point directly over an observer, with a speed of 600 miles per hour. The task is to find the rate at which the angle of elevation, theta, is changing when the angle equals 30 degrees.
What are the known variables in the problem?
-The known variables include the airplane's altitude (5 miles), the speed of the plane (600 miles per hour), and the angle of elevation at a certain point (30 degrees).
What is the relationship between the angle of elevation and the observer?
-The angle of elevation is the angle measured from a horizontal line to the observer's line of sight to the airplane. It is used to determine the position of the airplane relative to the observer on the ground.
How is the height of the airplane changing as it flies?
-The height of the airplane is not changing as it flies. The script confirms that the change in height (dh/dt) is zero since the airplane is flying horizontally at a constant altitude.
What is the significance of the horizontal distance (x) in the problem?
-The horizontal distance (x) is the distance from the observer to the point directly under the airplane. It is an important variable in determining the angle of elevation and is used in the calculation of the rate of change of the angle (d theta/dt).
How is the derivative of the tangent of theta with respect to time (d theta/dt) found?
-The derivative of the tangent of theta with respect to time is found using the secant squared rule, which states that the derivative of the tangent of an angle is the secant squared of that angle. This is applied to the equation derived from the given scenario.
What is the value of x when the tangent of theta equals 30 degrees?
-When the tangent of theta equals 30 degrees, x is calculated to be 8.66 miles by using the tangent function and the known height of the airplane.
What is the rate of change of the angle of elevation (d theta/dt) when theta is 30 degrees?
-The rate of change of the angle of elevation when theta is 30 degrees is found to be 30 radians per hour, or 600 degrees per hour, after applying the derived formula and substituting the known values.
Why is the cosine of 30 degrees used in the calculation?
-The cosine of 30 degrees is used in the calculation because it is a part of the derived formula for the rate of change of the angle of elevation. The cosine function relates the angle to the adjacent side of the triangle formed by the airplane, the observer, and the horizontal line.
How does the speed of the airplane affect the rate of change of the angle of elevation?
-The speed of the airplane directly affects the rate of change of the angle of elevation because as the airplane moves horizontally, it changes the horizontal distance (x) relative to the observer, which in turn affects the angle of elevation and its rate of change.
What is the role of the Pythagorean theorem in this problem?
-The Pythagorean theorem is not directly used in this problem because it relates to the sides of a right triangle, and the problem does not involve calculating the lengths of the sides but rather the rate of change of the angle of elevation with respect to time.
Outlines
🚀 Introduction to Airplane Elevation Angle Problem
The paragraph introduces a physics problem involving an airplane flying at an altitude of five miles towards a point directly over an observer. The airplane's speed is given as 600 miles per hour, and the task is to find the rate at which the angle of elevation, denoted as theta, is changing when theta equals 30 degrees. The speaker sets up the problem by discussing the variables involved, such as the height of the airplane (5 miles) and the unknown horizontal distance (x). The speed of the airplane is related to the rate of change in distance (dx/dt = 600 miles per hour). The speaker emphasizes understanding the variables and the relationship between them, particularly focusing on the angle of elevation and its relevance to the problem at hand.
📚 Derivation of the Rate of Change of Elevation Angle
In this paragraph, the speaker delves into the process of differentiating with respect to time to find the rate of change of the angle of elevation (d theta/dt). The speaker starts by establishing the relationship between the tangent of theta and the known variables (tangent of theta equals height over x, with height being 5 miles). The speaker then calculates the value of x when theta is 30 degrees, using the tangent function and finding x to be 8.66 miles. With the value of x known, the speaker proceeds to derive the equation for d theta/dt, incorporating the concepts of trigonometry and calculus. The derivation leads to the equation d theta/dt = -5 * cosine squared of theta / x squared. The speaker then substitutes the known values into this equation, including the derivative of x with respect to time (dx/dt = -600), and calculates the final value for d theta/dt to be 30 radians per hour, which is also expressed in degrees per hour for clarity.
🔢 Conclusion and Final Calculation
The final paragraph wraps up the problem by confirming the calculated rate of change of the angle of elevation. The speaker reiterates that the rate of change in theta (d theta/dt) with respect to time (t) is 30 degrees per hour, as derived from the previous calculations. This conclusion is a direct answer to the initial problem statement, providing the sought-after rate of change at the specified angle of 30 degrees. The speaker also acknowledges a minor error in the previous calculations but corrects it and reaffirms the final result, ensuring the audience's understanding of the problem-solving process and the final outcome.
Mindmap
Keywords
💡Airplane
💡Altitude
💡Angle of Elevation
💡Rate of Change
💡Tangent
💡Derivative
💡Secant
💡Pythagorean Theorem
💡Horizontal Line
💡Observer
💡Distance
💡Calculus
Highlights
Airplane flies at an altitude of five miles towards a point directly over an observer.
The speed of the plane is 600 miles per hour.
The objective is to find the rate at which the angle of elevation (θ) is changing when θ equals 30 degrees.
The height of the plane (h) is constant at 5 miles and does not change as the plane flies.
The horizontal distance (x) from the observer to the plane is unknown but can be determined using the tangent of the angle of elevation.
The rate of change of the horizontal distance (dx/dt) is equal to the speed of the plane, which is 600 miles per hour.
The tangent of the angle of elevation (tan(θ)) is equal to the height (h) divided by the horizontal distance (x).
At θ equals 30 degrees, the horizontal distance (x) is calculated to be 8.66 miles.
The general equation for the rate of change of θ with respect to time (t) involves the tangent and secant functions.
Differentiating with respect to t, the equation for dθ/dt involves the secant squared of θ and the negative reciprocal of x squared.
The height (h) is a constant value in the equation, which simplifies the process of finding the rate of change of θ.
The derivative of the cosine function with respect to θ is needed to find dθ/dt when θ is at 30 degrees.
Cosine of 30 degrees is equal to the square root of 3 divided by 2, or √3/2.
The final calculation for the rate of change of θ (dθ/dt) results in 30 radians per hour.
The result can also be expressed in degrees per hour, which is 600 degrees per hour.
The problem-solving approach involves a combination of geometry, trigonometry, and calculus.
The practical application of this problem could be in aviation for calculating rates of change in angles during flight.
The method used can be generalized for other problems involving rates of change in trigonometric functions.
Transcripts
Browse More Related Video
Related Rates - Angle of Elevation Problem

Solve related rates rising hot air balloon
Related Rates - Airplane Problems

Related rates: Approaching cars | Applications of derivatives | AP Calculus AB | Khan Academy

2019 AP Calculus AB & BC Free Response Question #1

Related Rate Problem # 2 - Aircraft Converging
5.0 / 5 (0 votes)
Thanks for rating: