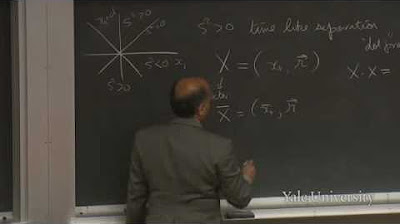13. Lorentz Transformation
TLDRIn this lecture, Professor Ramamurti Shankar delves into the intricacies of relativity, focusing on the Lorentz transformation and its implications on space and time. He explains how the velocity of light affects the perception of time and length, leading to time dilation and length contraction. The discussion includes thought-provoking examples such as the Twin Paradox and the moving meter stick, highlighting the relativity of simultaneity and the non-absolute nature of time and space. The lecture emphasizes the importance of understanding these concepts not just in terms of mathematical equations, but also their real-world applications and philosophical implications.
Takeaways
- 🕰️ The concept of time and space are relative and can vary for two observers moving relative to each other, a fundamental principle of relativity.
- 🚀 The velocity of light is constant for all observers, regardless of their relative motion, which is a key postulate of special relativity.
- 📐 Length contraction occurs for objects in motion relative to an observer, making the object appear shorter than its length at rest.
- 🕰️ Time dilation means that a clock will run slower for an observer in motion relative to another observer at rest, affecting the passage of time differently.
- 🌐 The transformation of space and time coordinates is described by the Lorentz transformation, which mixes space and time in a new way.
- 🔄 The relativistic addition of velocities does not follow the simple addition of classical mechanics but is modified by a factor involving the velocity of light.
- 💡 Understanding the relativistic effects requires thinking in terms of events and applying the Lorentz transformation to analyze differences in space and time coordinates.
- 🚄 The simultaneity of events is relative; two events that appear simultaneous to one observer may not be simultaneous to another observer in relative motion.
- 🛤️ Length contraction and time dilation are not just theoretical concepts but have practical implications, affecting the behavior of objects and the passage of time in high-speed situations.
- 🎯 The laws of relativity challenge classical notions of absolute space and time, introducing a new framework for understanding the universe.
- 🌟 The implications of relativity have been experimentally verified and are crucial for accurate predictions in high-speed and cosmological physics.
Q & A
What is the main concept being discussed in the transcript?
-The main concept discussed in the transcript is the relativity of space and time as observed from different frames of reference, including the Lorentz transformation, time dilation, length contraction, and the relativity of simultaneity.
How does the Lorentz transformation relate to the events observed by two different observers?
-The Lorentz transformation provides a mathematical framework to relate the observations of two observers moving relative to each other. It shows how the space and time coordinates of an event, as seen by one observer (S), are transformed into the coordinates seen by another observer (S prime) who is moving at a constant velocity relative to the first observer.
What is the significance of the gamma factor in the Lorentz transformation?
-The gamma factor is a crucial element in the Lorentz transformation. It accounts for the relativistic effects due to the relative motion between two observers. The gamma factor affects how time intervals (and hence, the rate of clocks) and lengths (such as meter sticks) appear to different observers. It ensures that the space and time coordinates transform correctly between different inertial frames.
How does time dilation work according to the transcript?
-Time dilation is a phenomenon where the passage of time is experienced differently by two observers moving relative to each other. The transcript explains that a clock in a frame of reference that is moving relative to another frame will appear to run slower from the perspective of the stationary observer. This effect is quantified by the Lorentz transformation and is a direct result of the invariance of the speed of light for all observers.
What is length contraction, and how does it relate to the observations of a moving object?
-Length contraction is the phenomenon where an object in motion appears to be shorter than when it is at rest, as observed from a different frame of reference. The transcript explains that the length of an object, such as a meter stick, will appear longest in its rest frame and will seem to contract for any observer who sees it moving. The degree of contraction is given by a factor that depends on the relative velocity between the observer and the moving object.
How does the concept of simultaneity change in the context of relativity?
-In the context of relativity, simultaneity is not an absolute concept. Two events that appear to occur simultaneously to one observer may not appear simultaneous to another observer moving at a different velocity. The transcript illustrates this with the example of two events happening at different locations, which can be made to appear simultaneous to a moving observer by sending a light pulse, but the stationary observer will disagree on the simultaneity due to the different times it takes for the light to reach each event location.
What is the Twin Paradox, and how is it explained in the transcript?
-The Twin Paradox is a thought experiment in special relativity that involves a pair of twins, one of whom makes a journey into space at high velocity and returns home to find that they have aged less than their twin who remained on Earth. The transcript explains that the paradox arises due to the relativity of simultaneity and time dilation. However, it is resolved by noting that the traveling twin experiences acceleration and deceleration during the trip, which means they do not have the same status as the twin who remained inertial. Thus, the relationship is not symmetrical, and the traveling twin will indeed be younger upon return.
What is the significance of the light clock in the discussion of time dilation?
-The light clock is a hypothetical clock that uses the speed of light to measure time intervals. It is significant because it provides a simple and clear demonstration of why moving clocks appear to run slower from the perspective of a stationary observer. Since the light clock operates based on the constant speed of light, any observer can agree on the path length and time it takes for light to travel, making it a useful model for illustrating time dilation effects.
How does the concept of length contraction resolve the paradox of a moving meter stick passing through a hole?
-The concept of length contraction resolves the paradox by showing that the moving meter stick appears shorter to the stationary observer. According to the stationary observer, the meter stick shrinks due to its motion, and thus it can pass through a hole that is smaller than its original length. However, from the perspective of the moving observer, the hole appears smaller, and the meter stick remains its original length. The paradox is reconciled by understanding that simultaneity is not absolute, and the two ends of the meter stick do not pass through the hole at the same time from the perspective of the moving observer.
What is the implication of the garage and car paradox mentioned in the transcript?
-The garage and car paradox illustrates the relativity of length contraction and simultaneity. If a car that is longer than the garage is moving at a speed that causes length contraction, there will be an instant when the entire car appears to fit inside the garage from the perspective of the moving car. However, from the perspective of the garage, the car never fully fits inside at once because the front enters before the back, causing a disagreement on whether the car was ever fully inside the garage. This paradox highlights the differences in simultaneity and length perception between moving and stationary observers.
How does the transcript address the issue of the relativity of simultaneity in the context of two events occurring in different locations?
-The transcript addresses the relativity of simultaneity by explaining that two events occurring at different locations may not be perceived as simultaneous by all observers due to their relative motion. It uses the example of light pulses sent from a moving train to demonstrate that a stationary observer on the ground will perceive the events as happening at different times, contrary to the perception of the observer on the train. This difference in perception is due to the fact that the space and time coordinates transform under the Lorentz transformation, leading to a relative concept of simultaneity.
Outlines
🌟 Introduction to Relativistic Event Observation
The paragraph discusses the concept of describing an event from the perspective of two observers, S and S', with S' moving relative to S. The event is synchronized in both observers' clocks at the moment they cross paths. The discussion introduces the idea of space and time coordinates being mixed in the relativistic view, contrasting with the classical notion of separate space and time coordinates. It also touches on the concept of length contraction and the relativity of simultaneity, hinting at the complexities that arise in the relativistic description of events.
🔄 Paradoxes in Relativistic Measurements
This paragraph delves into the paradoxes that arise from differing measurements of length and time between two observers in relative motion. It explores the concept that each observer perceives the other's measuring sticks as shortened and their clocks as running slower. The explanation includes a thought experiment with a light pulse and the derivation of the Lorentz transformation equations, which are fundamental to understanding the behavior of space and time in special relativity.
📐 The Lorentz Transformation and its Implications
The paragraph explains the Lorentz transformation equations, which relate the space and time coordinates of an event as observed by two observers in relative motion. It highlights the importance of these equations in understanding the relativistic effects such as length contraction and time dilation. The discussion also touches on the mathematical simplicity of the equations and their profound implications for our understanding of the universe, including the famous equation E=mc² and the Twin Paradox.
🤔 The Anomaly of Velocity and Rotation
This section discusses the analogy between the Lorentz transformation and a rotation in the coordinate system, highlighting the differences and the unique aspects of the Lorentz transformation. It addresses the student's confusion about the analogy and clarifies that while the transformation involves similar mathematical operations as rotation, it is not a simple rotation because it involves the mixing of space and time coordinates in a non-ordinary way.
🔄 Application of Lorentz Transformation to Event Differences
The paragraph focuses on applying the Lorentz transformation to the differences in space and time coordinates between two events, as observed by two different observers. It explains how the differences in coordinates also follow the Lorentz transformation rules, leading to the conclusion that the separation between two events appears different to observers in relative motion. The discussion also touches on the implications of this for understanding the nature of space and time in relativity.
🚀 Velocity Addition in Relativity
This section discusses the relativistic addition of velocities and how it differs from the classical addition of speeds. It explains that the velocity of light is the ultimate speed limit and cannot be exceeded by any object, no matter how the velocities are added. The example of firing a bullet from a moving train illustrates that the combined velocity cannot reach the speed of light, thus reinforcing the principles of relativity.
🕒 The Relativity of Simultaneity
The paragraph explores the concept of simultaneity in relativity, showing that two events that appear simultaneous to one observer may not be simultaneous to another observer moving at a different velocity. The discussion uses the thought experiment of two light pulses and the perception of their simultaneity from different frames of reference to demonstrate this concept. It emphasizes the relativistic view that simultaneity is not an absolute property but depends on the observer's motion.
⏳ Time Dilation and Clock Comparison
This section delves into the phenomenon of time dilation, where clocks in relative motion appear to run slower from the perspective of an observer at rest. The explanation involves the Lorentz transformation and the concept of proper time, highlighting that the time interval between two events as measured by a moving observer will appear longer compared to the time interval measured by an observer at rest. The discussion also touches on the implications of time dilation for the aging of objects and the famous Twin Paradox.
📏 Length Contraction and the Moving Meter Stick
The paragraph discusses the concept of length contraction, where an object in motion appears shorter than its length at rest. The explanation involves the Lorentz transformation and the operational definition of length, showing that the length of a moving object will be perceived differently by observers in relative motion. The discussion uses the example of a meter stick moving past a stationary observer and how the observer perceives the length of the stick differently, leading to the conclusion that length, like time, is relative.
🚗 The Paradox of the Moving Car and the Garage
This section presents a thought experiment involving a moving car and a garage, illustrating the relativistic effects of length contraction and the relativity of simultaneity. The discussion shows that under certain conditions, a car that is longer than the garage can fit inside due to length contraction at high velocities. However, the paradox arises from the disagreement between the observer who sees the car fitting inside and the one who sees the car breaking the garage due to the rear end not entering simultaneously. The explanation emphasizes the need to reconcile these differing perspectives based on the principles of relativity.
Mindmap
Keywords
💡Relativity
💡Lorentz Transformation
💡Space-Time
💡Simultaneity
💡Time Dilation
💡Length Contraction
💡Reference Frames
💡Velocity Addition
💡Clock Paradox
💡Speed of Light
💡Inertia
Highlights
Discussion of relativity and the concept of events as seen by two observers, S and S', with different frames of reference.
Explanation of how space and time coordinates can be combined to give new space and time coordinates, introducing the term 'coordinate' in a relativistic context.
Clarification on why time is considered a coordinate in relativity and how it differs from other coordinates.
Introduction to the Lorentz transformation and its implications on the understanding of space and time.
Discussion on the relativity of simultaneity, challenging the classical notion of absolute simultaneity.
Explanation of how velocities do not add in a simple way in relativity, leading to the conclusion that nothing can exceed the speed of light.
Illustration of the concept of length contraction and how it affects the perception of objects in motion.
Presentation of the famous Twin Paradox, highlighting the effects of time dilation on individuals moving at different velocities.
Discussion on the relativity of the length of objects, such as a meter stick, and how it changes depending on the observer's frame of reference.
Explanation of how simultaneity is not absolute and can vary for observers in different frames of reference.
Clarification on the concept of time dilation and its impact on the aging process of individuals and objects in motion.
Presentation of a thought experiment involving a light clock and the perception of time intervals by different observers.
Discussion on the operational definition of simultaneity and how it is affected by the relative motion of observers.
Explanation of the transformation equations for space and time coordinates and their implications on the understanding of relativity.
Discussion of the relativity of clock rates and how moving clocks appear to run slower compared to clocks at rest.
Presentation of the concept of length contraction and its paradoxical implications, such as a moving meter stick appearing shorter than its rest length.
Explanation of how the relative lengths of objects can be reconciled by understanding the operational definitions of measurement in different frames of reference.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: