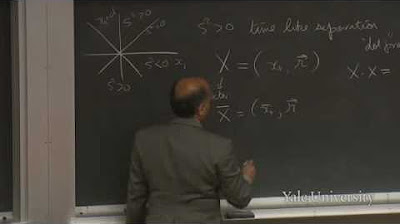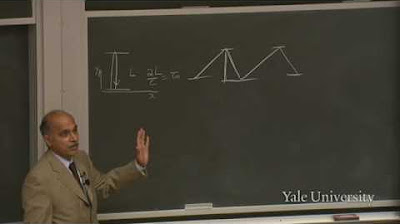Special Relativity | Lecture 1
TLDRIn this lecture from Stanford University, the professor delves into the intricacies of special relativity and classical field theory, emphasizing the importance of understanding classical mechanics as a foundation. The discussion covers the principle of relativity, the constancy of the speed of light, and the Lorentz transformations, which are crucial for grasping the behavior of objects moving at relativistic speeds. The lecture also explores the concepts of time dilation and length contraction, highlighting how they challenge traditional notions of space and time. Through the use of mathematical formulations and thought experiments, the professor provides a comprehensive overview of these fundamental theories in physics.
Takeaways
- 📚 The lecture introduces the concept of Special Relativity and Classical Field Theory, building upon previously learned concepts in Classical Mechanics and Quantum Mechanics.
- 🌟 The principle of relativity states that the laws of physics are the same in every inertial reference frame, which are frames where Newton's laws are correct and particles move with uniform velocity when不受力。
- 💡 Einstein added to the principle of relativity the law that the speed of light is constant in all inertial reference frames, leading to the conclusion that light must move with the same velocity in every frame.
- 🔄 The transformation laws between different reference frames need to be reevaluated to maintain the constancy of the speed of light, challenging the Newtonian assumption of absolute simultaneity.
- 🕒 The concept of simultaneity is frame-dependent, meaning that two events that are simultaneous in one reference frame may not be in another, moving reference frame.
- 🕓 The Lorentz transformations provide a mathematical framework to relate the space and time coordinates of one inertial reference frame to another, ensuring that the speed of light is observed as constant in all frames.
- 📏 The script discusses the concept of length contraction, where a meter stick moving relative to an observer appears shorter than when at rest, calculated by the factor √(1 - v²/c²).
- ⏳ Time dilation is introduced, with the moving observer's clock running slower than the stationary observer's clock, also calculated by the factor √(1 - v²/c²).
- 🛤️ The distinction between space-like and time-like separations of events in space-time is made, with space-like events being those where the spatial separation is greater than the time separation.
- 📌 The script touches on the idea of proper time, which is the time interval between two events as measured by a clock moving along the trajectory connecting those events, and is an invariant quantity in all reference frames.
- 🌐 The lecture concludes with a discussion on the implications of the Lorentz transformations for the motion of particles and the understanding of space-time geometry in the context of Special Relativity.
Q & A
What is the main focus of the course mentioned in the transcript?
-The main focus of the course is on special relativity and classical field theory, with an emphasis on understanding the relativistic aspect of phenomena such as light within the context of the special theory of relativity.
What did the students learn about in the previous quarter?
-In the previous quarter, the students learned about classical mechanics, including its general structure, the action principle, Hamiltonians, Lagrangians, and some elements of quantum mechanics.
Why is the study of light important in the context of relativity?
-The study of light is important in the context of relativity because light is a relativistic phenomenon that cannot be fully understood without the special theory of relativity. It is essential for grasping the principles of relativistic physics.
What is the principle of relativity?
-The principle of relativity states that for all coordinate systems related to each other by uniform velocity, the laws of physics are the same. In other words, all inertial reference frames have the same physical laws.
What is an inertial reference frame?
-An inertial reference frame is a coordinate system in which Newton's laws of motion are valid, and particles with no forces acting on them move with uniform velocity.
What is the relationship between moving reference frames in the context of special relativity?
-In the context of special relativity, moving reference frames are related by uniform motion relative to each other. The laws of physics must be the same in every inertial reference frame, and the transformation between these frames must account for the relativistic effects, such as time dilation and length contraction.
How does the speed of light play a role in the development of special relativity?
-The speed of light is a fundamental constant in special relativity. Einstein postulated that the speed of light is the same in all inertial reference frames, which led to the development of the theory as it requires a new understanding of space and time that is different from classical mechanics.
What is the concept of simultaneity in special relativity?
-The concept of simultaneity in special relativity is that the occurrence of two events that are simultaneous in one inertial frame may not be simultaneous in another inertial frame moving relative to the first. This is a result of the relative nature of time in different reference frames.
What is the Lorentz transformation?
-The Lorentz transformation is a set of mathematical equations that relate the space and time coordinates of an event as observed in two different inertial frames of reference. It is the foundation for understanding how space and time are interconnected in special relativity.
Why is it important to understand the Lorentz transformations in the study of relativity?
-Understanding the Lorentz transformations is crucial because they provide the mathematical framework for translating observations from one inertial frame to another while preserving the fundamental principles of relativity, such as the constancy of the speed of light.
What is the twin paradox in the context of special relativity?
-The twin paradox is a thought experiment in special relativity that involves one twin traveling at high speed relative to the other, who remains on Earth. When the traveling twin returns, they find that they have aged less than the twin who stayed at home. This paradox illustrates the effects of time dilation and the relativity of simultaneity.
Outlines
📚 Introduction to Special Relativity and Classical Field Theory
The lecture begins with an overview of the course content, focusing on special relativity and classical field theory. The speaker briefly recaps classical mechanics and quantum mechanics, noting the omission of the harmonic oscillator from the previous quarter. The goal is to study the relativistic end of physics, including the special theory of relativity and electromagnetic theory. The speaker confirms with the audience their desire to review special relativity, emphasizing its importance and foundational principles.
🌐 Reference Frames and the Principle of Relativity
The speaker delves into the concept of reference frames, explaining their role in classical mechanics and how they are defined by spatial coordinates and time. The discussion includes the idea of moving reference frames and the assumption of synchronized watches in pre-relativistic physics. The principle of relativity is introduced, stating that the laws of physics are the same in every inertial reference frame. This principle, while pre-existing Einstein, is combined with the constancy of the speed of light to form the basis of special relativity.
💡 The Paradox of Light Speed in Different Reference Frames
The lecture explores the paradox that arises when applying the principle of relativity to the speed of light. The speaker uses a thought experiment involving light rays and two observers in different reference frames to illustrate the contradiction that emerges when assuming the speed of light varies between these frames. This leads to the conclusion that the traditional assumptions about coordinate transformation and the nature of simultaneity must be reevaluated.
🕒 Redefining Simultaneity and Synchronization
The speaker challenges the traditional assumption of simultaneity across different reference frames, suggesting that it is frame-dependent. Using the example of synchronized clocks, the speaker explains Einstein's method of defining simultaneity through the synchronization of clocks using light signals. This redefines the concept of simultaneity and highlights the importance of carefully defining terms in the context of relativity.
📈 Visualizing Simultaneity in Moving Reference Frames
The lecture continues with a visual explanation of simultaneity in moving reference frames. The speaker describes how to represent light rays and moving observers on a coordinate system, emphasizing the need to draw light rays before anything else. The concept of a moving reference frame is introduced, with the speaker explaining how to plot the trajectory of a moving observer and how to determine the points of simultaneity according to Einstein's rules.
🌟 Synchronization and the Moving Observer
The speaker further elaborates on the synchronization of clocks in a moving reference frame. Using the example of three observers, the speaker demonstrates how light signals are used to synchronize clocks and how the concept of simultaneity differs between stationary and moving observers. The lecture also touches on the mathematical process of finding the intersection points that represent simultaneous events in different frames of reference.
🔄 The Lorentz Transformations and the Speed of Light
The speaker presents the Lorentz transformations, which are mathematical relationships that describe how space and time coordinates are related between two reference frames moving relative to each other. The transformations are derived from the postulates of special relativity, particularly the constancy of the speed of light in all inertial frames. The lecture explains how these transformations ensure that the speed of light is perceived as the same in every reference frame, resolving the earlier discussed paradox.
🕰️ Time Dilation and Length Contraction
The speaker discusses the phenomena of time dilation and length contraction, which are consequences of special relativity. Using the concept of proper time, the speaker explains how a moving clock appears to tick slower compared to a stationary clock. Similarly, a ruler moving through space appears shorter than when at rest. The lecture clarifies that these effects are not just apparent but are real and observable, and they apply to all types of clocks and measuring devices.
🤔 The Twin Paradox and Relativity Paradoxes
The speaker touches on the famous twin paradox, which is a thought experiment in special relativity that involves one twin traveling at high speed while the other remains on Earth. The paradox highlights the difference in elapsed time between the two twins due to the traveling twin's frame of reference moving at high velocity. The speaker also mentions other relativity paradoxes and sets the stage for further discussion on the motion of particles and the implications of relativity in future lectures.
🧐 The Hypotenuse and the Space-Time Distance
The speaker explores the concept of space-time distance in the context of special relativity, drawing parallels with Euclidean geometry. The lecture introduces the invariant quantity of space-time distance, which is the difference between the square of the time interval and the square of the spatial interval between two points. The speaker explains that this quantity, while seemingly different from traditional distance measurements, is a key element of relativistic space-time and has profound implications for understanding the behavior of objects in motion.
Mindmap
Keywords
💡Special Relativity
💡Classical Mechanics
💡Quantum Field Theory
💡Reference Frame
💡Lorentz Transformations
💡Time Dilation
💡Length Contraction
💡Inertial Reference Frame
💡Space-Time
💡Proper Time
Highlights
Introduction to the subject of Special Relativity and Classical Field Theory.
Discussion on the structure of Classical Mechanics and its principles.
Explanation of the Action Principle, Hamiltonians, and Lagrangians in Classical Mechanics.
Overview of the principles of Quantum Mechanics and its importance in understanding the harmonic oscillator.
The decision to focus on Quantum Mechanics and Quantum Field Theory in future quarters.
The goal of the quarter: to explore Special Theory of Relativity and Classical Field Theory.
The significance of light as a relativistic phenomenon and its relation to the Special Theory of Relativity.
Introduction to the concept of reference frames and their importance in understanding motion.
Explanation of how moving reference frames are perceived and their impact on the understanding of time.
The principle of relativity and its assertion that the laws of physics are the same in every inertial reference frame.
Discussion on the uniform motion of reference frames and its relevance to Newtonian mechanics.
The puzzle of the constancy of the speed of light in all reference frames and its implications.
The concept of simultaneity and its relativity in different reference frames.
Einstein's method of synchronizing clocks using light signals and its impact on the understanding of simultaneity.
The derivation of the Lorentz transformations and their role in ensuring the speed of light is constant in all reference frames.
Discussion on time dilation and space contraction as observed from moving reference frames.
The concept of proper time and its significance in understanding the space-time distance between two points.
Explanation of the space-like and time-like separation of points in space-time and their implications.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: