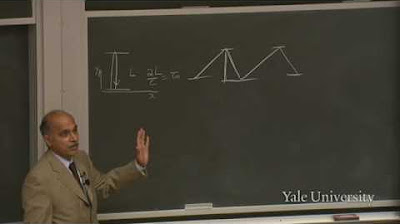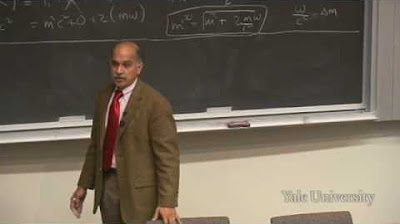14. Introduction to the Four-Vector
TLDRThe transcript is a detailed lecture on the principles of special relativity by Professor Ramamurti Shankar. It begins with a reminder of the importance of understanding Lorentz transformations, which are fundamental to the subject. The professor then delves into the concept of time dilation, explaining how a moving clock appears to tick slower from the perspective of a stationary observer. He also discusses length contraction, demonstrating how a moving object measures shorter in its direction of motion. The lecture continues with an exploration of the relativity of simultaneity and the consequences of causality in different frames of reference. The professor introduces the idea of the light cone, explaining how it defines the 'absolute future' and 'absolute past' in relation to an observer. He also touches on the concept of four-vectors and the space-time interval, which is invariant across different frames. The lecture concludes with a discussion on the four-momentum in relativity, differentiating it from classical momentum and highlighting its significance in understanding the energy of a moving particle. The content is rich with mathematical insights and thought-provoking examples that challenge the traditional Newtonian view of space and time, providing a comprehensive understanding of special relativity.
Takeaways
- 📚 The script is a lecture by Professor Ramamurti Shankar, focusing on the Lorentz transformations and their implications in special relativity.
- 🔍 The Lorentz transformations are key equations derived in the study of special relativity, which relate the space and time coordinates of an event as observed in two different inertial frames of reference.
- ⏱️ Time dilation is a consequence of the Lorentz transformations, where a clock moving relative to an observer appears to tick slower, emphasizing that time is relative and not absolute.
- 📏 Length contraction is also a result of the Lorentz transformations, meaning that the length of an object moving relative to an observer is measured to be shorter than its proper length.
- 🚀 The concept of lack of simultaneity is discussed, where events that appear simultaneous in one frame may not be perceived as simultaneous in another due to relative motion.
- 🔄 The lecturer uses the example of twins in different cities to illustrate the relativity of aging and the impossibility of absolute simultaneity in space-time events.
- 🛰️ The idea of causality and the order of events is explored, highlighting that if event A can cause event B, then A must occur before B in all frames of reference to avoid logical contradictions.
- 💡 The speed of light is established as an ultimate speed limit, with the theory of relativity demanding that no signal can travel faster than light to maintain logical consistency and causality.
- 📶 The light cone concept is introduced, dividing space-time into 'absolute future', 'absolute past', and a region where the order of events can vary between observers, but without causal contradictions.
- 📊 The script also delves into the mathematical elegance of special relativity, introducing the space-time interval as an invariant quantity that remains the same for all observers, regardless of their relative motion.
- 🧲 The analogy of rotations in Euclidean space is used to explain the Lorentz transformation's effect on space-time coordinates, emphasizing the symmetry and invariance of the space-time interval.
Q & A
What is the significance of Lorentz transformations in the context of the lecture?
-Lorentz transformations are fundamental to the lecture as they form the basis for all the concepts discussed, including time dilation, length contraction, and the lack of absolute simultaneity. The professor emphasizes that understanding these transformations is crucial for grasping the consequences of special relativity.
How does the Lorentz transformation equation for time difference (Δt') relate to time dilation?
-The Lorentz transformation for time difference (Δt') shows that a clock moving relative to an observer will appear to tick slower. This is known as time dilation, and it occurs because the term uΔx/c^2 affects the time interval measured by a stationary observer compared to the moving observer.
What is the concept of length contraction as explained in the lecture?
-Length contraction is the phenomenon where a stick moving relative to an observer appears shorter than its rest length (L_0). The lecture explains that the length measured by a stationary observer (L) is given by L_0 multiplied by the square root of (1 - v^2/c^2), indicating that the faster the stick moves, the shorter it appears.
How does the lecture illustrate the lack of absolute simultaneity?
-The lecture uses the example of twins born in different cities to illustrate that two events, which are simultaneous in one frame of reference, may not be simultaneous in another. This lack of absolute simultaneity is a direct consequence of the Lorentz transformations.
What is the 'light cone' concept introduced in the lecture?
-The 'light cone' is a visualization of the space-time regions that can be causally affected by an event. It consists of the 'absolute future' where events can be influenced by the initial event, the 'absolute past' where events can influence the initial event, and the 'relative future' where the order of events can be reversed depending on the observer's motion.
How does the lecture explain the relationship between causality and the order of events?
-The lecture explains that if event A can be the cause of event B, then it should not be possible for an observer to see event B occur before event A. This is ensured by the fact that if there is enough time for a light signal to travel from event A to event B, then no observer will see the events in reverse order.
What is the significance of the speed of light in the context of causality and signal transmission?
-The speed of light is significant because it sets a universal limit on the speed at which signals can travel and thus influence other events. According to the lecture, if there is not enough time for a light signal to travel from one event to another, then it is impossible for the first event to cause the second, ensuring no logical contradictions arise.
How does the lecture describe the transformation of coordinates in terms of X_0 and X_1?
-The lecture describes the Lorentz transformation in terms of X_0 (which is ct, a combination of time and the speed of light) and X_1 (which is the spatial coordinate x). It shows that under Lorentz transformations, X_1' = (X_1 - βX_0)/√(1 - β^2) and X_0' = (X_0 - βX_1)/√(1 - β^2), where β is the velocity u divided by the speed of light c.
What is the space-time interval and why is it invariant?
-The space-time interval is a measure of the 'distance' between two events in space-time, given by the quadratic function X_0^2 - X_1^2 - X_2^2 - X_3^2. It is invariant because all observers, regardless of their relative motion, will agree on its value. This invariance is a fundamental aspect of the space-time structure in special relativity.
How does the lecture explain the concept of the 'absolute future' and 'absolute past'?
-The 'absolute future' refers to events that are in the future light cone of an event, meaning they can be affected by signals traveling at or below the speed of light from the initial event. The 'absolute past' refers to events that are in the past light cone of an event, meaning they can influence the initial event. These concepts help to define the causal structure of space-time.
What is the difference between the space-time interval and the space interval?
-The space-time interval is a measure that combines both temporal and spatial separations between two events in a way that is invariant under Lorentz transformations. In contrast, the space interval refers to the spatial separation alone and does not account for time. The space-time interval can be positive, negative, or zero, unlike the space interval, which is always positive or zero.
Outlines
📚 Lorentz Transformations and Relativistic Effects
Professor Shankar emphasizes the importance of understanding Lorentz transformations as the foundation of relativistic physics. He explains how events appear different to observers moving at relative velocities, using the Lorentz transformation equations to derive the coordinates and time experienced by a moving observer. Key concepts such as time dilation, length contraction, and the lack of absolute simultaneity are introduced, highlighting the observer-dependent nature of time and space measurements.
🕰️ Time Dilation and Length Contraction
The script delves into the phenomena of time dilation and length contraction, illustrating how a moving clock appears to tick slower and a moving object seems shorter to a stationary observer. Shankar uses the Lorentz transformation to derive these effects and discusses the implications of reciprocity, where both observers perceive the other's clock as running slow. The explanation reinforces the relativity of motion and the constant speed of light for all observers.
🔄 The Relativity of Simultaneity and Causality
Shankar explores the concept of relativity of simultaneity, demonstrating that events deemed simultaneous in one frame of reference may not be perceived as such in another. He discusses the potential for logical contradictions arising from the reversal of event order in different frames, particularly when cause and effect are involved. The lecture stresses the importance of maintaining a consistent cause-effect relationship and the role of the speed of light as a limiting factor in preventing such contradictions.
🚀 The Impossibility of Superluminal Signaling
Building on the previous discussion, Professor Shankar explains that the theory of relativity demands no signal can travel faster than light to maintain logical consistency. He derives an equation that shows if two events are separated by a distance less than the time it takes for light to travel between them, an observer moving at a certain speed could perceive the events in reverse order. However, for causally connected events, the order must be preserved to avoid logical contradictions, thus establishing the light speed as an upper limit for signal transmission.
🌌 The Light Cone and the Structure of Space-Time
Shankar introduces the concept of the light cone to describe the causal structure of space-time. He explains how events within an observer's light cone are either in their absolute future or past and can be affected by or have affected the observer. The light cone illustrates the relativity of 'now' and the impossibility of influencing events outside of it, even with knowledge of their occurrence. This concept reinforces the idea that cause and effect cannot be reversed and that the speed of light is the ultimate speed limit.
🔗 The Invariant Space-Time Interval
The script discusses the invariant nature of the space-time interval, a quantity that remains constant across all frames of reference. Shankar explains that while observers may disagree on the individual space and time coordinates of an event, they will agree on the space-time interval. This concept is analogous to the invariant distance in Euclidean space, but with a crucial difference: in space-time, the interval involves the difference of squares, reflecting the non-Euclidean nature of space-time.
🧲 Four-Vector Formulation and Space-Time Symmetry
Shankar presents the four-vector notation for space-time coordinates, introducing a formalism that treats time and space on an equal footing. By defining X_0 as ct (time multiplied by the speed of light) and X_1 as the spatial coordinate x, he shows how the Lorentz transformation can be expressed in a symmetrical form for these 'space-time' coordinates. This formulation highlights the intrinsic symmetry of space-time and simplifies the transformation laws, making the equations more elegant and easier to handle in theoretical physics.
🛠️ The Four-Momentum and Relativistic Momentum
The script introduces the concept of four-momentum, a generalization of the classical momentum to relativistic contexts. Shankar defines four-momentum as the product of mass and four-velocity, where four-velocity is the rate of change of the position four-vector with respect to proper time. He explains how the components of four-momentum transform under Lorentz transformations, maintaining the vector's integrity across different frames of reference. This new definition of momentum incorporates both spatial and temporal aspects of motion into a single four-vector.
🚀 The Energy-Momentum Relation and Rest Energy
Shankar explores the relationship between energy and momentum in relativity, showing how the zero component of the four-momentum vector, P_0, is related to the energy of a particle. He derives an expression for the total energy of a moving particle, which includes both its rest energy (mc^2) and additional terms dependent on its velocity. This derivation reveals that even stationary particles possess energy, introducing the concept of rest energy, and highlights the continuous increase in kinetic energy as an object's velocity approaches the speed of light.
💥 Nuclear Reactions and the Conversion of Mass to Energy
The final paragraph discusses the practical implications of the energy-mass equivalence, particularly in the context of nuclear reactions. Shankar explains how the mass deficit observed in nuclear fusion or fission processes can be converted into energy, as described by Einstein's famous equation E=mc^2. This principle underlies the energy release in nuclear power and atomic bombs, although it's important to clarify that Einstein's work did not extend to the engineering of such applications.
🤔 Thought Experiment with Rockets and Relativistic Collisions
As a thought experiment, Shankar presents a scenario involving two rockets moving towards each other and questions whether a torpedo launched from one rocket would hit the other, as perceived by different observers. This problem challenges students to apply their understanding of relativity to a complex situation, considering the relative motion, length contraction, and time dilation to determine the outcome of the interaction from different perspectives.
Mindmap
Keywords
💡Lorentz transformations
💡Time dilation
💡Length contraction
💡Relativity of simultaneity
💡Causality
💡Light cone
💡Space-time interval
💡Four-vector
💡Invariant
💡Pseudo-Euclidean space
💡Proper time
Highlights
Lorentz transformations are fundamental to understanding the consequences of special relativity.
The equations for Lorentz transformations relate the coordinates of an event as observed in two different inertial frames of reference.
Time dilation is a direct consequence of Lorentz transformations, where a moving clock appears to tick slower from a stationary observer's perspective.
Length contraction is explained, showing that the length of an object moving relative to an observer is measured to be shorter than its proper length.
The concept of lack of simultaneity is introduced, indicating that events occurring simultaneously in one frame may not appear so in another.
The relativity of simultaneity is further explored with the example of twins born in different cities, highlighting the non-absolute nature of time.
The implications of Lorentz transformations on causality are discussed, emphasizing that cause and effect cannot be reversed.
The speed of light is established as an upper limit, with no signal allowed to travel faster, to maintain logical consistency in relativity.
The light cone concept is introduced, illustrating the regions of space-time that can affect or be affected by an event.
The absolute future and past are defined within the context of the light cone, determining which events can be influenced or have influenced the present.
The 'outside the light cone' defense is humorously presented as a legal strategy leveraging the impossibility of superluminal signaling.
The Lorentz transformation equations are rewritten in terms of four-vectors, simplifying the symmetry between space and time coordinates.
The space-time interval is defined as an invariant quantity, remaining constant across different frames of reference.
The distinction between time-like and space-like separations is made based on the sign of the space-time interval.
The four-momentum is introduced as a relativistic generalization of momentum, incorporating both spatial and temporal components.
The relationship between energy, momentum, and mass is explored, leading to the famous equation E=mc^2.
The practical applications of special relativity in understanding the behavior of particles at high velocities are discussed.
The thought experiment involving two rockets and a torpedo is presented to challenge students' understanding of relativistic effects.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: