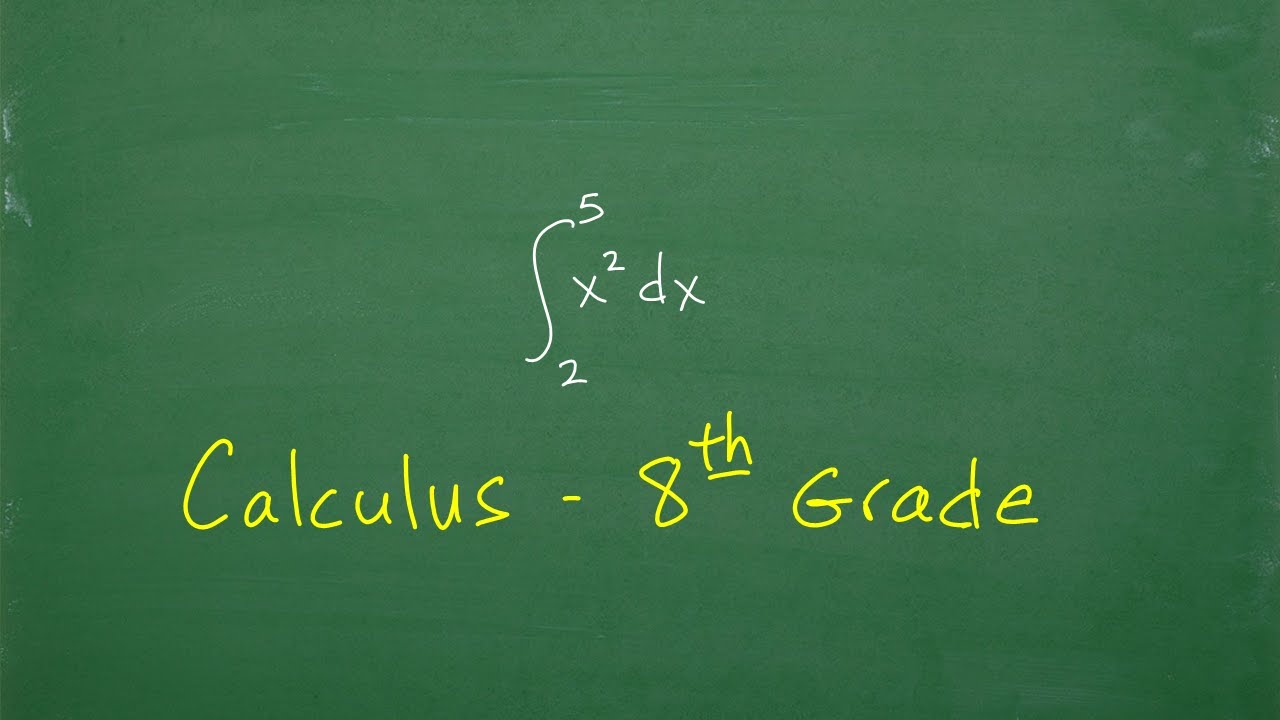EASY CALCULUS Introduction – Anyone with BASIC Math skills can understand….
TLDRThe video script introduces the viewer to the fundamental concepts of calculus, emphasizing its practical applications and demystifying its seemingly complex nature. The speaker, John, founder of Tablet Class Math, simplifies the integral concept by comparing it to a recipe and demonstrates how to calculate the area under a curve, specifically a parabola. He also stresses the importance of note-taking in mastering mathematics and promotes his online math help program. The video aims to inspire interest in calculus and数学, showcasing its relevance to solving real-world problems.
Takeaways
- 📚 The video is an introduction to calculus aimed at demystifying the subject and showing its practical applications.
- 🌟 Calculus is considered fascinating and intimidating by many, but it's accessible to anyone with basic math skills.
- 👨🏫 John, the founder of Tablet Class Math and a math teacher, presents the video to encourage interest in calculus.
- 🎓 The video explains the basic concept of an integral, which is a fundamental part of calculus and represents the sum of infinitely small parts.
- 🔢 The process of finding the integral of a function like x^n involves a simple recipe: add 1 to the power and divide by the new power.
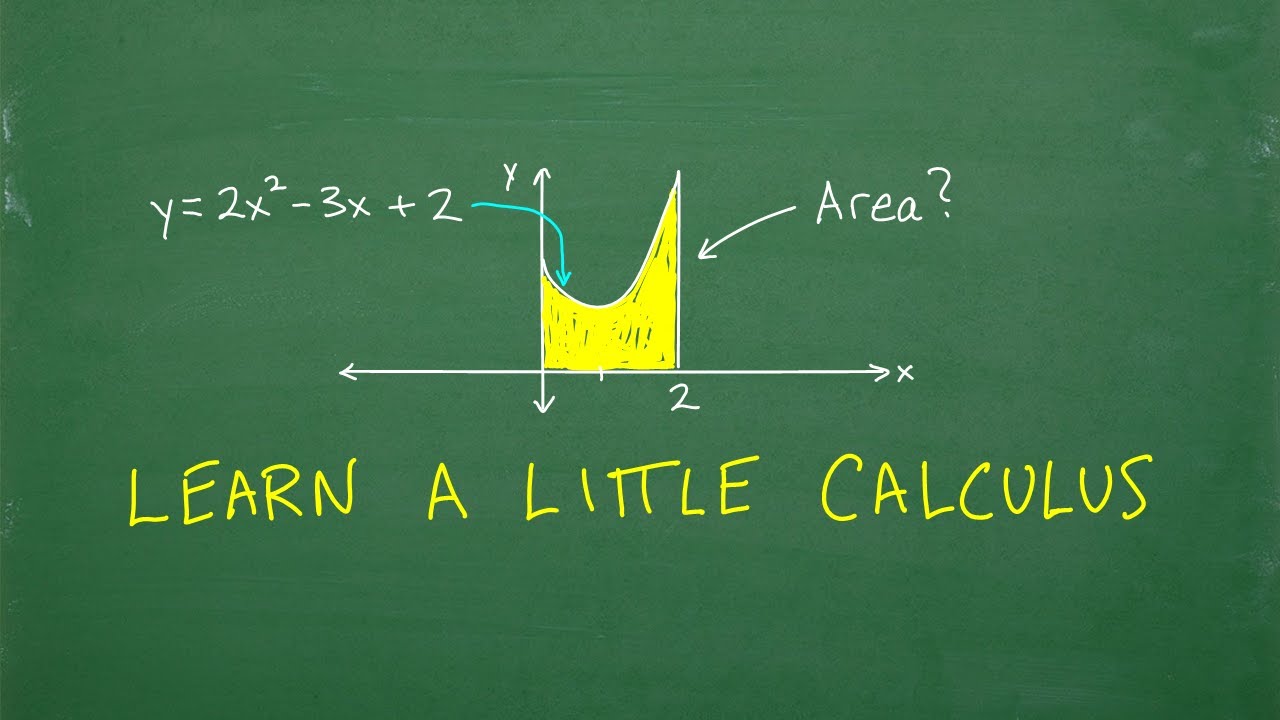
- 📈 The video demonstrates how to find the area under a curve, such as a parabola, using definite integrals.
- 📊 Finding the area under a curve is a practical application of calculus that is essential for solving problems with irregular shapes.
- 🥧 Calculus can be likened to a recipe book, providing formulas and rules to follow for various mathematical tasks.
- 📚 John emphasizes the importance of note-taking for learning and improving in mathematics, as it enhances focus and understanding.
- 🎥 The video is part of a larger collection of math courses and resources available for various levels of math learners, including test preparation and homeschooling.
- 💪 With motivation and interest, anyone can learn calculus, which has numerous applications in our modern world and is crucial for solving complex problems.
Q & A
What is the main topic of the video?
-The main topic of the video is an introduction to calculus, aiming to demystify the subject and explain basic concepts in a way that is accessible to everyone, regardless of their mathematical background.
What is the speaker's background and what does he offer?
-The speaker, John, is the founder of Tablet Class Math and a middle and high school math teacher. He has created an online math help program with over a hundred math courses ranging from pre-algebra to advanced levels. He also offers test preparation materials for various exams and helps independent learners like homeschoolers.
What is the significance of understanding the language of mathematics in learning calculus?
-Understanding the language of mathematics is crucial in learning calculus because it allows one to interpret and apply mathematical symbols and concepts correctly. Just like learning a new language opens up new ways of communication, understanding mathematical language is key to grasping and utilizing calculus effectively.
What is an integral in calculus?
-An integral in calculus is a mathematical operation that represents the process of summing up an infinite number of infinitesimally small elements, often used to calculate areas under curves, volumes of solid figures, and other quantities that are not easily found using basic arithmetic.
What is the rule for finding the indefinite integral of x to the power of n?
-The rule for finding the indefinite integral of x to the power of n is to increase the power by one and then divide by the new power. Mathematically, the integral of x^n dx is x^(n+1)/(n+1) + C, where C is the constant of integration.
How does the speaker simplify the concept of finding the area under a curve?
-The speaker simplifies the concept by comparing it to adding up tiny rectangle slivers under the curve. By summing these infinitesimally small rectangles, one can find the area under a curve, which is a fundamental application of calculus.
What is the practical application of calculus demonstrated in the video?
-The practical application of calculus demonstrated in the video is finding the area under a curve, specifically under a parabola described by the equation y = x^2, between 0 and 2 on the x-axis.
How does the speaker calculate the area under the parabola y = x^2 from 0 to 2?
-The speaker calculates the area by applying the definite integral of x^2 from 0 to 2. He uses the rule for the indefinite integral of x^2, which is x^3/3 + C, and then evaluates this at the bounds 2 and 0 to find the definite integral, resulting in an area of 8/3 or approximately 2.67.
What advice does the speaker give to those interested in improving their math skills?
-The speaker advises that note-taking is the foundational way to improve in mathematics. He emphasizes that students who take comprehensive and focused notes tend to do very well. He also encourages holding oneself accountable and actively focusing during math classes to avoid distractions.
What is the speaker's recommendation for learning calculus?
-The speaker recommends that anyone interested in learning calculus should start by taking pre-calculus, which he considers a prerequisite for understanding calculus concepts. He also suggests taking calculus in a college classroom setting for a more in-depth and structured learning experience.
How does the speaker describe the power of calculus in solving real-world problems?
-The speaker describes calculus as a powerful tool for solving a wide range of technical problems in the modern world. It has infinite applications and is essential for understanding and calculating areas and volumes of complex shapes that cannot be easily determined using basic arithmetic or geometric formulas.
Outlines
📘 Introduction to Calculus
The speaker introduces the topic of calculus, acknowledging its reputation as an intimidating subject. Despite this, the speaker aims to demystify calculus by explaining its basic concepts in a way that is accessible to everyone, regardless of their mathematical background. The speaker emphasizes the importance of understanding the language of mathematics and offers a brief overview of their own background as a math teacher and creator of an online math help program. The speaker also touches on the practical applications of calculus and its significance in the modern world.
📚 Breaking Down Calculus Fundamentals
The speaker delves into the fundamentals of calculus, focusing on the concept of an integral. Using an informal and relatable approach, the speaker explains the integral symbol and its role in adding things up. The explanation includes a practical example of finding the integral of x squared, using a step-by-step process that resembles following a recipe. The speaker emphasizes that calculus, while challenging, is not beyond reach and can be understood by anyone willing to learn.
📊 Applying Calculus to Real-World Problems
The speaker illustrates the practical application of calculus by discussing how it can be used to find the area of shapes for which there are no straightforward formulas. Using the example of a parabolic curve, the speaker explains how calculus can help determine the area under a curve, which is a common problem in various fields. The explanation includes a brief overview of how to use integrals to sum up infinitesimally small rectangles under a curve to find the total area, showcasing the power and utility of calculus.
🔢 Calculating Areas Using Definite Integrals
The speaker continues the discussion on applying calculus to find areas, specifically focusing on the use of definite integrals. By using the example of the parabolic curve (y = x^2), the speaker demonstrates how to calculate the area under the curve between two points (0 to 2). The process involves evaluating the integral at the upper and lower bounds of the interval and subtracting the results. The speaker provides a clear step-by-step calculation, highlighting the method's applicability to finding areas under curves for different ranges.
🚀 Encouraging the Study of Calculus
In the concluding paragraph, the speaker encourages viewers to consider studying calculus, emphasizing its fascinating nature and wide range of applications. The speaker shares personal experiences of inspiring students to develop an interest in mathematics and progress to more advanced studies, including calculus. The speaker suggests that while calculus can be complex, it is accessible with motivation and interest. The speaker also invites viewers to explore their YouTube channel and online math help program for further learning resources, and expresses gratitude for the viewers' time and engagement.
Mindmap
Keywords
💡Calculus
💡Integral
💡Note-taking
💡Pre-calculus
💡Applications of Calculus
💡Area
💡Parable
💡Definite Integral
💡Math Help Program
💡Test Preparation
💡Homeschooling
Highlights
Introduction to Calculus aimed at beginners and those interested in the topic.
Calculus is fascinating and can be understood even by those with basic math skills.
The speaker, John, is the founder of Tablet Class Math and an experienced math teacher.
John has created an online math help program with over a hundred math courses.
Note-taking is emphasized as a key method for improving in mathematics.
The concept of an integral is introduced as a way to add things up, symbolized by the elongated S.
The rule for finding the indefinite integral of x to the n power is explained.
A practical problem of finding the area under a curve is discussed as an application of calculus.
The area under a curve is found by summing up infinitesimally small rectangles under the curve.
The definite integral is introduced to find the area under the x squared graph from 0 to 2.
The process of evaluating the definite integral by substituting values is demonstrated.
Calculus is described as a powerful tool for finding areas and volumes of various shapes.
John encourages viewers to consider studying calculus for its numerous applications in the modern world.
The importance of motivation and interest in learning calculus is highlighted.
John's Math Help Program is promoted as a resource for those needing assistance in mathematics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: