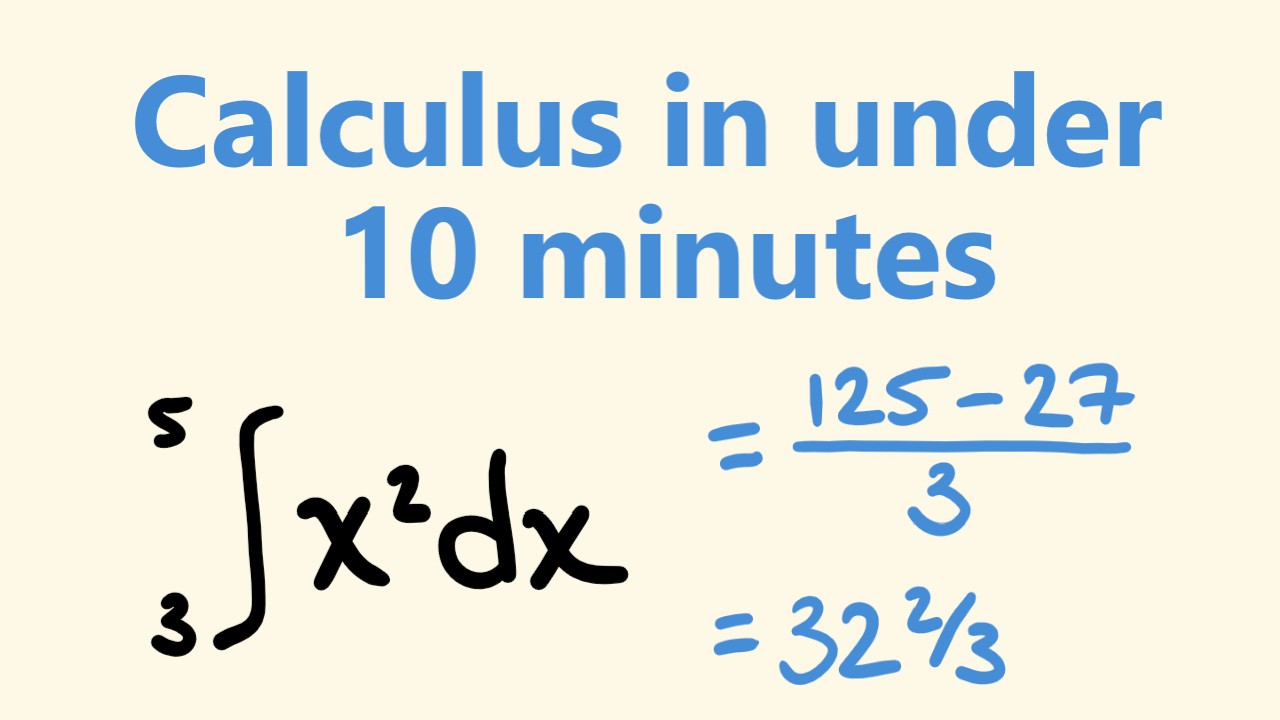Calculus – taught at the 8th grade level
TLDRThis video script offers an accessible introduction to calculus, tailored for middle school students with basic algebra knowledge. Hosted by John, the founder of TC Math Academy, the script demystifies calculus by explaining its real-world applications, particularly in solving area and rate of change problems. John simplifies complex concepts, guiding viewers through an actual calculus problem to find the area under a curve, using both an estimation method and a precise integral calculation. The script encourages students to embrace calculus, emphasizing that with the right instruction and effort, anyone can master it.
Takeaways
- 📚 Calculus is an advanced branch of mathematics typically studied at the college level, often by engineers and scientists.
- 🔍 The script aims to demystify calculus by teaching it at an eighth-grade level, assuming basic algebra knowledge.
- 👋 John, the founder of TC Math Academy and a middle/high school math teacher, introduces himself and offers resources for math assistance.
- 🎯 The two main problems calculus solves are calculating areas and volumes of irregular shapes and determining instantaneous rates of change.
- 📏 Calculus is essential for modern technological advancements, such as space travel and the development of cell phones.
- 📈 The script explains the concept of a function and how to graph it, which is fundamental to understanding calculus.
- 📉 The process of estimating the area under a curve using rectangles is introduced as a precursor to the concept of integration in calculus.
- 🔢 The importance of making rectangles 'infinitely small' to find an exact area under a curve is highlighted as the core of calculus.
- ✅ The script demonstrates how to perform a basic integral to find the exact area under the curve of a function, using the function f(x) = x^2 as an example.
- 📝 The power of calculus is shown by comparing the estimated area under a curve to the exact area calculated using calculus.
- 🌟 The video concludes with encouragement that anyone can learn calculus with the right mindset and step-by-step approach to building math skills.
Q & A
What is the main topic of the video script?
-The main topic of the video script is an introduction to calculus, aimed at an eighth-grade level, explaining the basics and its applications.
Who is the speaker in the video script?
-The speaker in the video script is John, the founder of TC Math Academy and a middle and high school math teacher.
What are the two main problems that calculus solves according to the script?
-The two main problems that calculus solves are finding the area and volume of irregular shapes for which there is no formula, and determining the rate of change, such as the instantaneous speed of an object.
What is the significance of calculus in modern day applications as mentioned in the script?
-According to the script, calculus is significant in modern day applications as it has been used by engineers and scientists to solve technical problems, enabling advancements like space travel and the development of technology such as cell phones.
How does the script simplify the concept of calculus for middle school students?
-The script simplifies the concept of calculus by relating it to basic middle school math concepts like the area of rectangles and by using the idea of breaking down areas under curves into smaller rectangles to approximate the total area.
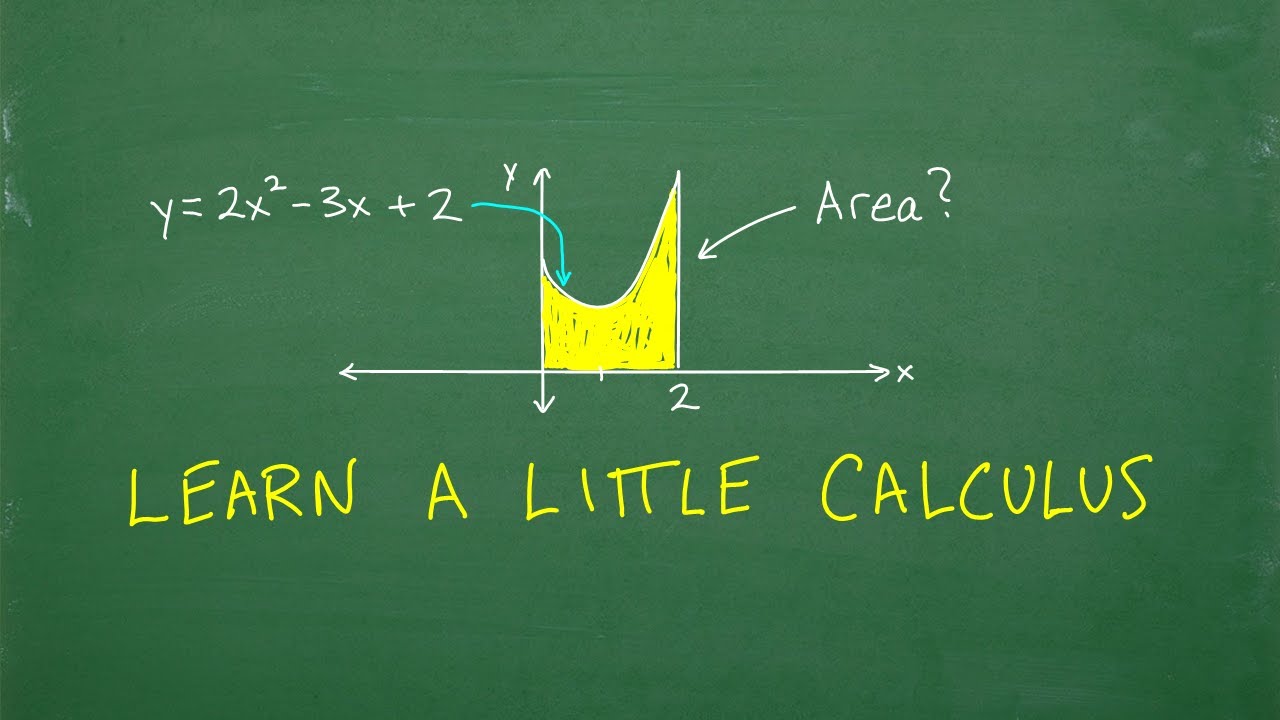
What is the 'area problem' in calculus as described in the script?
-The 'area problem' in calculus refers to the challenge of finding the area under a curve for shapes that do not have a straightforward formula for calculating area, which calculus helps to solve.
What is the concept of 'rate of change' in calculus as explained in the script?
-The concept of 'rate of change' in calculus is about finding the instantaneous rate at which something is changing, such as the exact speed of a car at a specific moment in time, which calculus can determine.
How does the script use rectangles to explain the approximation of an area under a curve?
-The script uses the idea of approximating the area under a curve by dividing it into rectangles. The width of these rectangles is constant, and the height is determined by the value of the function at specific points, which are then used to estimate the total area.
What is the function given in the script to demonstrate the concept of a function and its graph?
-The function given in the script is f(x) = x^2, which is used to demonstrate how a function can be represented graphically as a parabola and how points on the graph can be found by plugging in x values into the function.
How does the script describe the process of finding the exact area under a curve using calculus?
-The script describes the process as using calculus to sum up infinitely small rectangles (or strips) under the curve from one point to another, which is represented by the integral notation and involves applying calculus rules to find the exact area.
What is the final step in calculating the exact area under the curve in the script?
-The final step in calculating the exact area under the curve in the script involves evaluating the integral of the function from one to two, and then subtracting the integral evaluated at one from the integral evaluated at two to find the precise area.
What advice does the speaker give to those who might be intimidated by calculus?
-The speaker advises that anyone can handle calculus if they are excited about it and build up their basic math skills step by step, emphasizing that calculus is a learnable language and not to be intimidated by the notation.
Outlines
📚 Introduction to Calculus for Beginners
The script introduces the concept of calculus, aimed at an eighth-grade level, ensuring that anyone with basic algebra can understand. The speaker, John, founder of TC Math Academy and a math teacher, offers a basic crash course on calculus. He discusses the importance of calculus in modern society, particularly for engineers and scientists, and how it is essential for solving technical problems. The video promises to demystify calculus, covering its essence and even solving a calculus problem, all within 15 to 20 minutes. John also introduces his math health program for students at various levels and those preparing for math-related tests.
📐 Understanding Calculus: Area and Rate of Change
This paragraph delves into what calculus is and its applications. It explains that calculus is an advanced branch of mathematics crucial for professionals like engineers and scientists. The script simplifies the concept by focusing on two main problems that calculus solves: calculating areas and volumes of irregular shapes for which there are no direct formulas (the area problem), and determining the instantaneous rate of change, such as the speed of a car at a specific moment in time (the rate of change problem). The paragraph sets the stage for a practical example that will demonstrate these concepts in the context of an actual calculus problem.
📈 The Fundamentals of Functions and Graphs
The script introduces the concept of functions, using the example of 'f(x) = x squared', and explains how to graph and interpret them. It describes the process of finding points on the graph of a function by substituting values of x into the function's formula. The explanation is tailored for middle school students, assuming familiarity with variables and basic algebra. The paragraph emphasizes the importance of understanding functions and their graphical representation as a foundation for grasping calculus problems that will be introduced later in the script.
📝 Estimating Area Under a Curve Without Calculus
The script discusses a method to estimate the area under a curve when one does not know calculus. It suggests approximating the area by dividing the curve into rectangles and calculating the area of each rectangle, then summing these areas for an overall estimate. The example uses the function f(x) = x squared and divides the area under the curve from x=1 to x=2 into three equal parts, estimating the height of each rectangle using the function's values at specific x-coordinates. This approach is a precursor to the more precise methods of calculus that will be introduced later.
🔍 Refining the Area Estimation with Infinitesimal Rectangles
The script explains how to refine the area estimation under a curve by using infinitely small rectangles, which is the fundamental concept behind calculus. It contrasts this with the previous rough estimation and illustrates that by making the rectangles infinitely small, one can achieve a more accurate approximation of the area. The paragraph introduces the notation for integration in calculus and explains that the process involves summing up these infinitesimally small rectangles to find the exact area under the curve of the function f(x) = x squared from x=1 to x=2.
📘 Calculating the Exact Area Using Integration
This paragraph demonstrates the process of finding the exact area under a curve using calculus, specifically integration. It walks through the steps of integrating the function f(x) = x squared, which involves adding one to the power of x and then dividing by that new number to find the antiderivative. The script then applies the fundamental theorem of calculus to evaluate the definite integral from x=1 to x=2, resulting in the exact area. The calculation is simplified for understanding, emphasizing that calculus provides a precise method for solving problems that were previously only estimable.
🚀 Embracing the Power of Calculus and Encouragement for Learning
The final paragraph reflects on the power of calculus and its ability to provide exact solutions to complex problems. It contrasts the earlier estimation with the precise calculation obtained through calculus, showing the significant difference and the value of exact answers. The script encourages viewers not to be intimidated by calculus, comparing it to learning a new language, and emphasizes that with excitement and step-by-step learning, anyone can master it. It concludes by wishing the viewers well in their mathematical endeavors and inviting them to engage with the content by liking and subscribing.
Mindmap
Keywords
💡Calculus
💡Middle School Math
💡Algebra
💡Function
💡Area Problem
💡Rate of Change
💡Instantaneous
💡Integration
💡Estimation
💡Infinitesimal
Highlights
Introduction to calculus aimed at an 8th-grade level, ensuring accessibility for those with basic algebra knowledge.
The essence of calculus is taught, including its applications and importance in fields like engineering and science.
Calculus is defined as an advanced mathematics course typically taken by engineers and scientists.
The significance of calculus in modern technology, such as space travel and cell phones, is discussed.
Two main problems calculus solves: finding areas of irregular shapes and calculating instantaneous rates of change.
An example of calculating the area under a curve using basic algebra as an introduction to the concept of integration.
The concept of a function and its graphical representation is explained to build a foundation for understanding calculus.
Demonstration of how to find points on a curve using a function, which is crucial for understanding calculus problems.
Introduction to the process of estimating the area under a curve using rectangles as a precursor to understanding integration.
Explanation of how to refine the area estimation by using thinner rectangles to better approximate the curve.
The fundamental concept of calculus is revealed: using infinitely small rectangles to find the exact area under a curve.
A step-by-step guide on how to perform a basic integral to find the exact area under the curve of x squared.
Calculus rules are simplified for easier understanding, focusing on the process of integration.
The power of calculus is demonstrated by comparing the estimated area with the exact area calculated using calculus.
Emphasis on the learnability of calculus and encouragement for viewers to overcome the intimidation of its notation.
Final thoughts on the importance of building up basic math skills to eventually handle calculus successfully.
Closing remarks encouraging viewers to pursue their mathematical adventures with confidence.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: