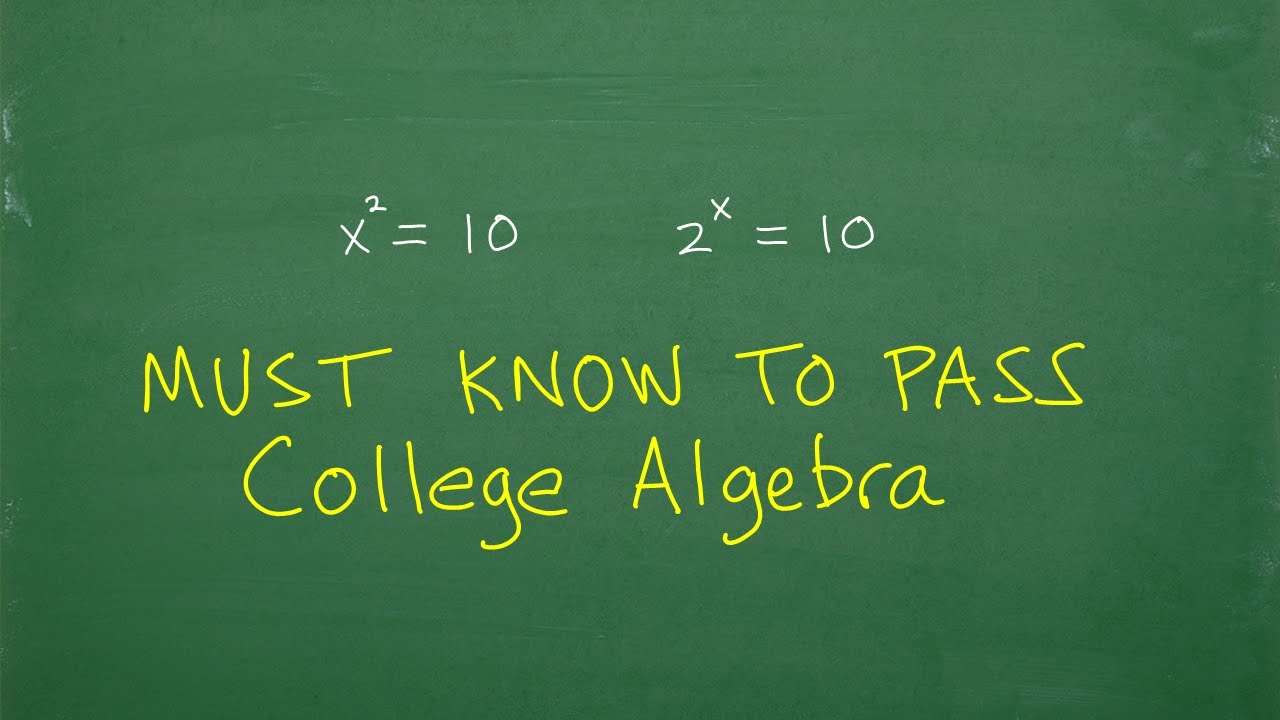Want to PASS Algebra? You better know this formula

TabletClass Math
26 Oct 202117:19
EducationalLearning
32 Likes 10 Comments

TLDRIn this informative video, John, the founder of Tablet Class Math, introduces and explains the quadratic formula, a crucial tool in algebra and higher-level mathematics. He emphasizes its importance and provides a step-by-step guide on how to apply it to solve quadratic equations, using the example of 3x^2 - 6x + 2 = 0. John also discusses his online math classes and resources, encouraging viewers to enhance their math skills and offering further assistance through his program.

Takeaways
  • 📝 The script introduces a quadratic equation (3x^2 - 6x + 2 = 0) and emphasizes the importance of a key formula in algebra and beyond.
  • 🧠 The 'secret formula' referred to is the quadratic formula, which is crucial for solving quadratic equations and should be memorized for long-term use.
  • 📈 The quadratic formula is presented as x = (-b ± √(b^2 - 4ac)) / (2a), applicable for any quadratic equation in the form ax^2 + bx + c = 0.
  • 🔢 The script provides a step-by-step walkthrough of applying the quadratic formula to the given equation, highlighting the need for precision and attention to detail.
  • 📊 It is emphasized that quadratic equations always have two solutions, and the quadratic formula is a powerful tool for finding them.
  • 👨‍🏫 The speaker, John, is the founder of Tablet Class Math and a middle and high school math teacher, offering online math classes and resources.
  • 📚 John's program can assist students in their math classes, providing additional instruction and math notes beyond his full courses.
  • 🌐 The video description contains links to various math course descriptions and resources for further learning.
  • 🚫 The script advises against common mistakes such as not using parentheses when plugging values into the quadratic formula and attempting to cross-cancel incorrectly.
  • 🎓 The quadratic formula is highlighted as a fundamental tool for any level of math, with applications in higher-level mathematics.
  • 💪 The message is to learn and internalize the quadratic formula for future mathematical endeavors.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the quadratic formula and its application in solving quadratic equations.

  • What is the quadratic formula?

    -The quadratic formula is used to solve quadratic equations in the form of ax^2 + bx + c = 0, and it is given by x = (-b ± √(b^2 - 4ac)) / (2a).

  • What is the significance of the quadratic formula in mathematics?

    -The quadratic formula is significant because it provides a general solution to quadratic equations, which are widely encountered in various fields of mathematics and science.

  • What is the first step in solving a quadratic equation using the quadratic formula?

    -The first step is to ensure that the equation is in standard form, which is ax^2 + bx + c = 0, with the highest power of x being squared.

  • How does the speaker introduce himself in the video?

    -The speaker introduces himself as John, the founder of Tablet Class Math and a middle and high school math teacher who has created numerous online math classes.

  • What are the three techniques mentioned for solving quadratic equations?

    -The three techniques mentioned are taking the square root of both sides, factoring, and using the quadratic formula.

  • Why is it important to memorize the quadratic formula?

    -It is important to memorize the quadratic formula because it is extremely useful and has wide applications in various levels of mathematics, making it an essential tool for anyone studying math.

  • What does the discriminant (b^2 - 4ac) represent in the quadratic formula?

    -The discriminant determines the nature of the roots of the quadratic equation. It helps to identify whether the solutions are real and distinct, real and repeated, or complex.

  • How does the speaker emphasize the importance of checking your work when using the quadratic formula?

    -The speaker emphasizes double-checking your work to ensure that all values are plugged into the formula correctly, especially noting the importance of using parentheses and handling negative signs to avoid errors.

  • What is the final result of the example problem 3x^2 - 6x + 2 = 0?

    -The final result of the example problem is x = (3 ± √(3))/3, which simplifies to two solutions: x = 1 + √3/3 and x = 1 - √3/3.

  • What additional resources does the speaker offer for those needing more help with math?

    -The speaker offers a variety of online math classes, a large library of courses, and math notes for further assistance and practice.

Outlines
00:00
📚 Introduction to the Quadratic Formula

The speaker, John, introduces the topic of the quadratic formula, emphasizing its importance in algebra and higher mathematics. He presents a quadratic equation as an example and encourages viewers to attempt solving it. John shares his background as the founder of Tablet Class Math and a middle and high school math teacher. He mentions his extensive online math classes and offers assistance through his program for various math courses. He also provides math notes for viewers.

05:02
🧠 Understanding the Quadratic Equation

John explains the given quadratic equation, identifying it as a polynomial with the highest power of two. He discusses three primary techniques for solving quadratic equations, highlighting that the quadratic formula is essential for those not easily factored or involving irrational numbers. He emphasizes the need to memorize the quadratic formula for its broad applications in mathematics.

10:02
🔢 Applying the Quadratic Formula

The speaker demonstrates how to apply the quadratic formula to the given equation, explaining the standard form required and the importance of using parentheses when plugging in values. He carefully walks through the steps of the calculation, including simplifying the discriminant and solving for the variable x. John stresses the importance of double-checking work to avoid errors and provides a clear, step-by-step breakdown of the process.

15:03
🎓 Final Solutions and Encouragement

John presents the final solutions to the quadratic equation, highlighting that there are two unique solutions. He reiterates the significance of the quadratic formula for future mathematical studies and encourages viewers to utilize his video playlist and math health program for further instruction. He concludes by wishing viewers well in their mathematical endeavors and offers his thanks for their time.

Mindmap
Keywords
💡Quadratic Equation
A quadratic equation is a polynomial equation of degree two, which typically takes the form ax^2 + bx + c = 0. In the video, the equation 3x^2 - 6x + 2 = 0 is an example of a quadratic equation. The speaker emphasizes the importance of recognizing and solving such equations, which are fundamental in algebra and higher levels of mathematics.
💡Secret Formula
The 'secret formula' referred to in the video is the quadratic formula, a fundamental tool for solving quadratic equations. The speaker builds suspense around this formula, highlighting its importance and encouraging viewers to commit it to long-term memory. The quadratic formula is presented as a solution to the given quadratic equation.
💡Quadratic Formula
The quadratic formula is a general method for solving quadratic equations and is expressed as x = (-b ± √(b^2 - 4ac)) / (2a). It is crucial for solving any quadratic equation that does not factor easily or cannot be solved by taking the square root directly. In the video, the quadratic formula is applied to the example equation to find its solutions.
💡Algebra
Algebra is a branch of mathematics that uses symbols and rules to solve equations. In the context of the video, algebra is the subject area where quadratic equations and the quadratic formula are foundational concepts. The speaker is a math teacher who provides online classes and emphasizes the importance of understanding algebra for further mathematical studies.
💡Factoring
Factoring is the process of breaking down a polynomial into its factors, which are simpler expressions that multiply together to give the original polynomial. In the video, the speaker mentions that factoring is a technique to solve quadratic equations, but it is not applicable to the example equation given.
💡Discriminant
The discriminant is the part of the quadratic formula under the square root, denoted as b^2 - 4ac. It determines the nature of the roots of a quadratic equation. If the discriminant is positive, the equation has two distinct real roots; if it is zero, there is exactly one real root; and if it is negative, the equation has two complex roots.
💡Mathematics Adventures
The term 'mathematics adventures' is used metaphorically in the video to describe the learning journey in mathematics. It implies that studying math can be an exciting and challenging experience, full of problem-solving and discovery. The speaker uses this term to encourage viewers to pursue their studies in math with enthusiasm.
💡Math Health Program
The Math Health Program mentioned in the video is an online educational resource created by the speaker. It is designed to provide structured instruction and assistance to students taking math courses, such as algebra and beyond. The program includes a variety of math classes and notes to help students succeed in their mathematical studies.
💡Standard Form
In the context of the video, standard form refers to the conventional way of writing a quadratic equation, which is with the highest power term first, followed by the lower power terms, and finally a constant term, all set equal to zero. This format is essential for applying the quadratic formula correctly.
💡Solving Quadratics
Solving quadratics refers to the process of finding the solutions or roots of a quadratic equation. The video focuses on the quadratic formula as a method for solving quadratics, especially when other methods like factoring or taking the square root are not applicable. The speaker provides a detailed explanation and steps on how to use the quadratic formula to solve the given quadratic equation.
Highlights

The speaker introduces a secret formula that is crucial for anyone studying algebra or higher-level mathematics.

The example problem given is a quadratic equation: 3x^2 - 6x + 2 = 0.

The speaker is John, founder of Tablet Class Math and a middle and high school math teacher with extensive experience in creating online math classes.

John emphasizes the importance of memorizing the quadratic formula for long-term memory due to its extensive applications in mathematics.

The quadratic formula is presented in its standard form: x = (-b ± √(b^2 - 4ac)) / (2a).

The speaker explains that the quadratic formula is applicable to all quadratic equations, which always have two solutions.

John provides a detailed step-by-step guide on how to apply the quadratic formula to the example problem.

The process of solving the quadratic equation involves identifying the coefficients a, b, and c from the equation.

The speaker highlights the importance of using parentheses when plugging values into the quadratic formula to avoid errors.

The discriminant (b^2 - 4ac) is introduced as part of the quadratic formula process, which helps determine the nature of the roots.

John demonstrates how to simplify the quadratic formula by factoring out the greatest common factor and simplifying radicals.

The final solutions to the example problem are x = (3 + √3) / 3 and x = (3 - √3) / 3, showcasing the two unique solutions of a quadratic equation.

The speaker offers additional resources, including more videos and math notes, for those who need further assistance with the quadratic formula.

John's teaching approach focuses on clear explanations and emphasizes the importance of understanding the mechanics behind the formulas.

The transcript serves as both an educational resource and an advertisement for John's math programs and services.

Transcripts

Browse More Related Video

100% Certainty you will see this in ALGEBRA

Want to PASS College Algebra? Absolutely, better understand this…

Your First Basic CALCULUS Problem Let’s Do It Together….

Get The Help You Need To Succeed In Math!

Terrible at Factoring trinomials? Do this…

Learn Functions – Understand In 7 Minutes

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuadraticFormulaMathTeachingAlgebraTipsEducationalContentMathematicsTutorialOnlineMathClassesMiddleSchoolMathHighSchoolMathCollegeAlgebraMathematicsAdventures