Your First Basic CALCULUS Problem Let’s Do It Together….
TLDRThe video introduces the subject of calculus, emphasizing its importance and beauty despite its reputation for being advanced and difficult. The speaker, John, founder of Tablet Class Math, explains basic concepts such as integration and derivatives, using the example of a ball's trajectory to illustrate how calculus can determine the maximum altitude. He also discusses the significance of good math notes for students and offers his online math help program for further assistance.
Takeaways
- 📚 Introduction to Calculus: The video aims to introduce viewers to the subject of calculus, emphasizing its reputation as advanced and difficult, yet beautifully understandable and powerful.
- 🤔 Understanding Concepts: The key concepts and principles of calculus are accessible to anyone, and the video seeks to demystify these ideas for the viewer.
- 📈 Calculus and Real-World Applications: Calculus is highlighted as a fundamental tool in various fields, including physics and engineering, and is crucial for modern technology.
- 👨🏫 About the Instructor: The speaker, John, introduces himself as the founder of Tablet Class Math and a middle and high school math teacher with years of experience.
- 🎓 Online Math Help: John offers an online video-based math help program, which is comprehensive and caters to various math levels, including middle and high school.
- 📒 Importance of Math Notes: The video emphasizes the importance of having good math notes for students, as it correlates with better math grades.
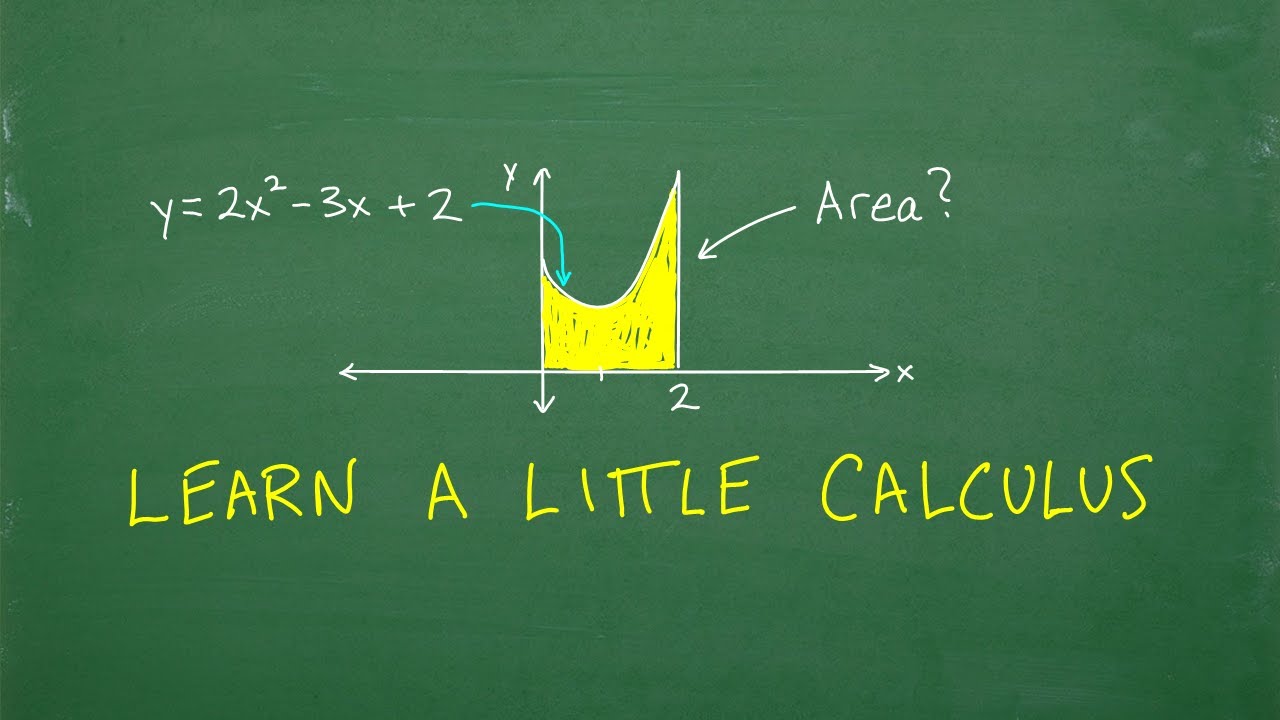
- 🔍 Problem Solving: A problem involving a ball's trajectory is presented to illustrate the power of calculus in finding maximum altitude, which is a basic yet effective example.
- 📊 Parabolic Shapes and Algebra: The video briefly touches on parabolic shapes and how algebra can be used to find the vertex of a parabola, which represents the maximum point.
- 🚀 Calculus Concepts: The two primary concepts of calculus, integration and derivatives, are introduced, with the focus on using derivatives to find the slope and maximum points.
- 📚 Derivative as Slope: The first derivative of a function is explained as a formula for the slope, which helps in determining the maximum or minimum points of a curve.
- 🔢 Solving for Maximum: A step-by-step process of using the first derivative to find when the slope is zero (the maximum point) is demonstrated using a simple quadratic equation.
- 🎯 Final Point: The video concludes with the location of the maximum point of the parabola at (-4, 7), illustrating the practical application of calculus.
Q & A
What is the main topic of the video?
-The main topic of the video is an introduction to calculus, specifically focusing on how to use calculus to find the maximum altitude of a ball thrown into the air.
Why is calculus considered advanced and difficult?
-Calculus is considered advanced and difficult because it involves complex concepts and principles that require a strong foundation in algebra and other areas of mathematics. However, the video aims to show that these concepts are understandable and even beautiful.
What are the two primary concepts learned in calculus?
-The two primary concepts learned in calculus are integration and differentiation, often referred to as the derivative.
How does integration relate to the problem discussed in the video?
-Integration is related to finding the area under a curve, which is not directly used in the problem discussed in the video. However, it is one of the key concepts in calculus and has many applications in various fields.
What is the role of the derivative in the context of the video?
-The derivative is used to find the slope of the curve at any given point. In the context of the video, it is used to determine the point at which the slope is zero, which corresponds to the maximum altitude of the ball.
How does the speaker introduce the concept of slope in relation to the problem?
-The speaker introduces the concept of slope by comparing it to the angle and steepness of a line. He uses the analogy of a roller coaster to explain how the slope changes from positive (going up), to zero (at the top), and then to negative (going down).
What is the equation of the first derivative found in the video?
-The equation of the first derivative found in the video is negative two x minus eight, written as -2x - 8. This represents the slope of the parabola at any point along the x-axis.
How does the speaker find the maximum point of the parabola?
-The speaker finds the maximum point of the parabola by setting the first derivative (the slope) equal to zero and solving for x. He finds that the maximum occurs at x = -4. Then, he plugs this value back into the original function to find the corresponding y-coordinate, which is 7.
What is the significance of the point (-4, 7) in the context of the problem?
-The point (-4, 7) represents the maximum altitude of the ball thrown into the air. At x = -4 on the x-axis, the ball reaches its highest point, which is 7 units high on the y-axis.
How does the speaker relate the concepts of calculus to real-world applications?
-The speaker relates the concepts of calculus to real-world applications by mentioning that without calculus, modern technology such as cell phones and airplanes would not exist. He emphasizes that calculus has solved many technical problems and is fundamental to our understanding of the world.
What resources does the speaker offer for those interested in learning more about calculus?
-The speaker offers an online video-based math help program, which includes comprehensive lessons on solving common problems at various levels of mathematics. He also provides detailed math notes covering pre-algebra, algebra, geometry, and trigonometry.
Outlines
📚 Introduction to Calculus
The video begins with an introduction to calculus, acknowledging its reputation as an advanced and challenging subject. The speaker, John, emphasizes that despite its complexity, the concepts and principles of calculus are understandable and beautiful. He aims to showcase the power of calculus through a basic but interesting problem, suitable for those new to the subject. John also introduces himself as the founder of Tablet Class Math and a middle and high school math teacher, offering an online video-based math help program. He invites viewers to check out his program and math notes, which cover a range of topics from pre-algebra to trigonometry.
📈 Understanding Calculus Concepts: Integration and Derivative
In this paragraph, John explains the two primary concepts of calculus: integration and the derivative. Integration is introduced as a method to find the area under a curve, while the derivative is related to the slope of a curve. He uses the analogy of a roller coaster to illustrate how the slope changes, with the maximum point (vertex) being where the slope is zero. John prepares the viewer for a problem that will use calculus to find the maximum altitude of a ball's trajectory, represented by a parabolic shape.
🧮 Calculating the First Derivative
John demonstrates how to calculate the first derivative of a function, which provides the formula for the slope of the curve at any point. He walks through the process of finding the first derivative of a quadratic equation, using algebraic manipulations and explaining the rules involved. The first derivative is shown to be a formula that can be used to determine where the slope of the curve is zero, which corresponds to the maximum point of the parabola.
📊 Finding the Maximum Point of a Parabola
Here, John applies the concept of the first derivative to find the maximum point of a parabola. He sets the derivative equal to zero to find the x-coordinate where the slope is zero, indicating the peak of the parabola. By solving the equation, he finds that the maximum occurs at x = -4. He then plugs this value back into the original function to find the corresponding y-coordinate, which is 7. Thus, the vertex of the parabola is at (-4, 7). John reiterates that this is a basic illustration of using calculus to solve problems and encourages viewers to appreciate the subject's fundamental concepts.
🙌 Conclusion and Encouragement
John concludes the video by encouraging viewers to engage with his content and consider subscribing to his YouTube channel for more math videos. He emphasizes the importance of calculus in modern technology and expresses his passion for teaching math. John invites viewers to follow the links in the video description for further help with math and wishes everyone the best in their mathematical endeavors.
Mindmap
Keywords
💡Calculus
💡Integration
💡Derivative
💡Parabolic Shape
💡Slope
💡Maximum Altitude
💡Algebra
💡Math Notes
💡Online Math Help
💡Roller Coaster
Highlights
Calculus is a powerful branch of mathematics with a reputation for being advanced and difficult, yet its concepts and principles are understandable and beautiful.
The video aims to introduce viewers to the power of calculus through a basic but interesting problem that even beginners can solve along.
Algebra is used in this problem, but it's basic and even those unfamiliar with algebra can learn something from the video.
John, the founder of Tablet Class Math and a middle and high school math teacher, has created a comprehensive online video-based math help program.
Good math notes are essential for math students, and those with the best notes often have the best grades.
The problem discussed involves a ball being fired into the air, and the goal is to find at what point the ball reaches its maximum altitude.
Calculus can be used to find the maximum of a shape, such as the vertex of a parabola.
Integration and differentiation (the derivative) are two primary concepts learned in calculus.
Integration is used to find the area under a curve, while the derivative is used to find the slope of a curve at any given point.
The slope of a curve changes along its length, and the derivative allows us to find the exact slope at any point, such as the vertex of a parabola.
The vertex of a parabola is the point where the slope is zero, which is the maximum or minimum point.
To find the maximum altitude of the ball, the first derivative of the function representing the ball's path is used.
The first derivative gives a formula for the slope, and setting this equal to zero helps find the vertex of the parabola.
The process of finding the first derivative involves taking the highest power term and applying the power rule, which involves multiplying by the exponent and then decreasing the exponent by one.
After finding the first derivative, solving the equation where the derivative equals zero gives the x-coordinate of the vertex.
Substituting the x-coordinate back into the original function gives the y-coordinate of the vertex, determining the maximum point of the parabola.
This example illustrates the practical application of calculus in solving real-world problems, such as the trajectory of a projectile.
Calculus is fundamental to modern technology, including cell phones and airplanes, and learning it can lead to a deeper appreciation for the subject and its applications.
The video encourages viewers to explore calculus further and offers resources for those interested in learning more about the subject.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: